Çarpma kuralı iki veya daha fazla fonksiyonun çarpımının türevinin hesaplanmasında kullanılan bir yöntemdir. Kuralı Gottfried Leibniz türettiği için bu kural Leibniz kuralı olarak da geçer. Kuralın matematiksel ifadesi f ve g sırasıyla f(x) ve g(x) ifadelerinin kapalı formu olmak üzere şöyle verilir:
İspat
Türevin tanımı kullanılarak iki fonksiyonun çarpımının türevine bakılırsa
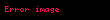
Genelleme
F fonksiyonu N tane birbirinden farklı ancak aynı değişkene bağlı fonksiyonun çarpımı olsun.
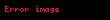
Bu ifadenin türevi yukarıda yapılan ispata dayanılarak şu şekilde gösterilir:
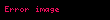
Çarpımın ifadesindeki i, 1 'den N 'ye kadar k hariç her değeri alır.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Carpma kurali iki veya daha fazla fonksiyonun carpiminin turevinin hesaplanmasinda kullanilan bir yontemdir Kurali Gottfried Leibniz turettigi icin bu kural Leibniz kurali olarak da gecer Kuralin matematiksel ifadesi f ve g sirasiyla f x ve g x ifadelerinin kapali formu olmak uzere soyle verilir ddx fg dfdx g f dgdx displaystyle frac d dx fg left frac df dx right g f left frac dg dx right IspatTurevin tanimi kullanilarak iki fonksiyonun carpiminin turevine bakilirsa ddx fg limh 0f x h g x h f x g x h limh 0f x h g x h f x g x h f x g x h f x g x h limh 0g x h f x h f x h f x g x h g x h g x f x f x g x displaystyle begin alignedat 4 frac d dx fg amp lim h to 0 frac f x h g x h f x g x h amp lim h to 0 frac f x h g x h f x g x h f x g x h f x g x h amp lim h to 0 g x h frac f x h f x h f x frac g x h g x h amp g x f x f x g x end alignedat GenellemeF fonksiyonu N tane birbirinden farkli ancak ayni degiskene bagli fonksiyonun carpimi olsun F x i 1Nfi x displaystyle F x prod i 1 N f i x Bu ifadenin turevi yukarida yapilan ispata dayanilarak su sekilde gosterilir dFdx k 1Nfk i kNfi displaystyle frac dF dx sum k 1 N f k prod i neq k N f i Carpimin ifadesindeki i 1 den N ye kadar k haric her degeri alir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
