Gerilme, fizikte, ip, kablo, zincir veya demir çubuk, kafes kiriş gibi üç boyutlu cisimlere her iki uçtan uygulanan çekme kuvveti olarak tanımlanmaktadır. Atomik seviyede, atom veya moleküller birbirinden ayrılıp elektromanyetik potansiyel enerji kazandığında, gerilme oluşur. Gerilmiş olan çubuk veya ip eski konumlarına gelebilmek için uçlarına bağlanıp germe uygulayan objeleri ters bir kuvvetle çekecektir. Sıkıştırmanın tersi gerilmedir. Fizikte, gerilme bir kuvvet olmamasına rağmen, Newton veya pound-kuvvet birimleriyle tanımlanmaktadır. İp veya tel gibi objeler, uçlarına bağlanıp gerilmelerini sağlayan objelere tersi yönde kuvvet uygularlar. Gerginlikten dolayı oluşan bu kuvvetlere germe kuvveti denilmektedir. İp veya tellerin bağlı olduğu objelerde; ivmenin sıfır olduğu dengede olan veya ivmelenmenin ve kuvvetin olduğu iki olası sistem vardır.
Tek Boyutlu Sistemlerde Gerilme
Gerilme, negatif olmayan bir sayısal büyüklüktür. Sıfır gerilme objenin gevşek durumda olduğunu belirtir. İp veya halatlar genellikle kütlesi olmayıp sadece uzunluğu olan tek boyutlu objeler olarak Kabul edilir. İp de kasnaklardan ya da titreşimlerden kaynaklı esnemeler yoksa, gerilme uçlardan uygulanan kuvvetlere eşit olacak şekilde ip boyunca sabittir. Newton'un üçüncü yasasına göre, iplere uç noktalarından uygulanan kuvvetler aynıdır. Bir ip, bir ya da daha fazla makaranın etrafında dönüyorsa, makara kütlesinin ve sürtünmenin yok sayıldığı ideal koşullarda tüm ip boyunca gerilme sabittir. Titreşen bir ip, üzerindeki gerilmeye bağlı olarak bir dizi frekansla titreşim gerçekleştirir. Bu frekanslar Newton un yasalarından elde edilir. Mikroskopik seviyede her ip parçası ip boyunca gerilmeye eşit olacak şekilde bir kuvvetle birbirlerini çekerler. İp boyunca gerçekleşen gerilme T(X) olarak gösterilir. X, ip üzerindeki herhangi bir noktadır. İp de kavislenme varsa, ip parçasına her iki komşu ip parçasından etki eden çekmeler sıfır olmaz ve yay parçası üzerinde net bir kuvvet oluşur. Net kuvvet, ivmelenmeye sebep olur. Ayrıca, net kuvvet dengeleyici olup; yayın hareketi, teorisinde yer alan enine dalgaları içerir: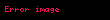
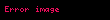

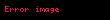
Üç Boyutlu Sistemlerde Gerilme

Gerilme, demir çubuk veya kafes kiriş gibi üç boyutlu malzemelerin uç noktalarına uygulanan kuvveti tanımlamak içinde kullanılmaktadır. Gerilme etkisiyle demir çubuk uzar. Yük ve uzama miktarı, tek başına kuvvetten ziyade kesit alanın etki eden her kuvvete bağlı olarak malzemede deformasyonda sebep olabilir. Bu sebeple, gerilme = eksenel kuvvet / kesit alanı ifadesi mühendislik uygulamaları için daha kullanışlıdır. Gerilme, 3x3 matris boyutunda tensör olarak belirtilir. Gerilme tensörü elemanı olan 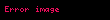
Denge Sistemi
Etki eden kuvvetlerin toplamı sıfır ise, sistem dengededir.
Örneğin, yaya bağlı olan bir objenin sabit hızda düşey olarak T gerginliğinde sarkıtıldığını düşünelim. Sistem sabit bir hıza sahip ve sonuç olarak dengede çünkü yaydaki gerilme (objeyi yukarı çekme etkisi) yer çekimi kuvvetine (objeyi aşağıya çekme etkisi, mg) eşittir.
Net Kuvvet Altındaki Sistem
Dengede olmayan bir kuvvet etki ettiği zaman, sistem net bir kuvvete sahip olur. Tüm kuvvetlerin toplamı sıfır değildir. İvme ve net kuvvet her zaman bir arada bulunmaktadır.
Örneğin, yukarıda belirtilen aynı sistemi düşünelim fakat, objenin artan bir hızla aşağıya doğru sarkıtıldığını kabul edelim (artan ivmelenme). Sonuç olarak, sistemde net bir kuvvet bulunmaktadır. Bu durumda azalan ivmelenme 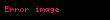
Diğer örnekte, 
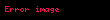




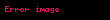

Modern Fizikte İpler
Rölativistik teorideki ip benzeri objeler, mesela modern ip teorisinde kullanılan veya kuarklar arasındaki etkileşim modellerinde kullanılan ipler gibi, gerilmeye sahiptirler. Enerji ip uzunluğuyla orantılıdır. Sonuç olarak, bu tip iplerde gerilme, uzama miktarından bağımsızdır. Uzayabilen iplerde, Hooke Yasası uygulanır.
Kaynakça
- ^ a b c d Giancoli, Douglas C. (2008). "Section 5.7.". Physics for Scientists and Engineers with Modern Physics (7. bas.). Pearson Education. ISBN . 20 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 27 Aralık 2020.
- ^ Fetter, Alexander L.; Walecka, John Dirk (2003). Theoretical Mechanics of Particles and Continua. Dover Books on Physics. Courier Corporation. ISBN . 19 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 27 Aralık 2020.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Gerilme fizikte ip kablo zincir veya demir cubuk kafes kiris gibi uc boyutlu cisimlere her iki uctan uygulanan cekme kuvveti olarak tanimlanmaktadir Atomik seviyede atom veya molekuller birbirinden ayrilip elektromanyetik potansiyel enerji kazandiginda gerilme olusur Gerilmis olan cubuk veya ip eski konumlarina gelebilmek icin uclarina baglanip germe uygulayan objeleri ters bir kuvvetle cekecektir Sikistirmanin tersi gerilmedir Fizikte gerilme bir kuvvet olmamasina ragmen Newton veya pound kuvvet birimleriyle tanimlanmaktadir Ip veya tel gibi objeler uclarina baglanip gerilmelerini saglayan objelere tersi yonde kuvvet uygularlar Gerginlikten dolayi olusan bu kuvvetlere germe kuvveti denilmektedir Ip veya tellerin bagli oldugu objelerde ivmenin sifir oldugu dengede olan veya ivmelenmenin ve kuvvetin oldugu iki olasi sistem vardir Tek Boyutlu Sistemlerde GerilmeGerilme negatif olmayan bir sayisal buyukluktur Sifir gerilme objenin gevsek durumda oldugunu belirtir Ip veya halatlar genellikle kutlesi olmayip sadece uzunlugu olan tek boyutlu objeler olarak Kabul edilir Ip de kasnaklardan ya da titresimlerden kaynakli esnemeler yoksa gerilme uclardan uygulanan kuvvetlere esit olacak sekilde ip boyunca sabittir Newton un ucuncu yasasina gore iplere uc noktalarindan uygulanan kuvvetler aynidir Bir ip bir ya da daha fazla makaranin etrafinda donuyorsa makara kutlesinin ve surtunmenin yok sayildigi ideal kosullarda tum ip boyunca gerilme sabittir Titresen bir ip uzerindeki gerilmeye bagli olarak bir dizi frekansla titresim gerceklestirir Bu frekanslar Newton un yasalarindan elde edilir Mikroskopik seviyede her ip parcasi ip boyunca gerilmeye esit olacak sekilde bir kuvvetle birbirlerini cekerler Ip boyunca gerceklesen gerilme T X olarak gosterilir X ip uzerindeki herhangi bir noktadir Ip de kavislenme varsa ip parcasina her iki komsu ip parcasindan etki eden cekmeler sifir olmaz ve yay parcasi uzerinde net bir kuvvet olusur Net kuvvet ivmelenmeye sebep olur Ayrica net kuvvet dengeleyici olup yayin hareketi teorisinde yer alan enine dalgalari icerir ddx t x dr x dx v x r x w2s x r x displaystyle frac d dx bigg tau x frac d rho x dx bigg v x rho x omega 2 sigma x rho x v x displaystyle v x birim uzunluktaki kuvvet sabiti w2 displaystyle omega 2 yaydaki r x displaystyle rho x kadar enine gerceklestirilen yerdegistirme rezonanslarinin ozdegeri Yayli calgilardaki cesitli harmonic hareketlerde yukaridaki teoride aciklanabilmektedir Uc Boyutlu Sistemlerde GerilmeGerilmenin uc boyutlu uzayda gosterimi Gerilme demir cubuk veya kafes kiris gibi uc boyutlu malzemelerin uc noktalarina uygulanan kuvveti tanimlamak icinde kullanilmaktadir Gerilme etkisiyle demir cubuk uzar Yuk ve uzama miktari tek basina kuvvetten ziyade kesit alanin etki eden her kuvvete bagli olarak malzemede deformasyonda sebep olabilir Bu sebeple gerilme eksenel kuvvet kesit alani ifadesi muhendislik uygulamalari icin daha kullanislidir Gerilme 3x3 matris boyutunda tensor olarak belirtilir Gerilme tensoru elemani olan s11 displaystyle sigma 11 gerilme kuvvetinin alana oranidir veya sikistirmanin alana oranidir Sikistirmada negative sonuc vardir ancak skaler olarak aynidir Denge SistemiEtki eden kuvvetlerin toplami sifir ise sistem dengededir F 0 displaystyle sum vec F 0 Ornegin yaya bagli olan bir objenin sabit hizda dusey olarak T gerginliginde sarkitildigini dusunelim Sistem sabit bir hiza sahip ve sonuc olarak dengede cunku yaydaki gerilme objeyi yukari cekme etkisi yer cekimi kuvvetine objeyi asagiya cekme etkisi mg esittir F T mg 0 displaystyle sum vec F vec T m vec g 0 Net Kuvvet Altindaki SistemDengede olmayan bir kuvvet etki ettigi zaman sistem net bir kuvvete sahip olur Tum kuvvetlerin toplami sifir degildir Ivme ve net kuvvet her zaman bir arada bulunmaktadir F 0 displaystyle sum vec F neq 0 Ornegin yukarida belirtilen ayni sistemi dusunelim fakat objenin artan bir hizla asagiya dogru sarkitildigini kabul edelim artan ivmelenme Sonuc olarak sistemde net bir kuvvet bulunmaktadir Bu durumda azalan ivmelenme mg gt T displaystyle mg gt T olarak belirtilir F T mg 0 displaystyle sum vec F T mg neq 0 Diger ornekte m1 displaystyle m 1 ve m2 displaystyle m 2 kutlelerine sahip birbirlerine sirasiyla surtunmesiz bir makara uzerinden gecen iple baglanan A ve B cisimlerini dusunelim A cismi B cisminden daha agir ise m1 gt m2 displaystyle m 1 gt m 2 A cismine etki eden iki kuvvet vardir kendisini asagiya ceken kutlesi w1 m1g displaystyle w 1 m 1 g ve ipteki yukari dogru ceken gerilme T displaystyle T Sonuc olarak A cismi uzerindeki net kuvvet F1 displaystyle F 1 w1 T displaystyle w 1 T dir Bu sebeple m1a m1g T displaystyle m 1 a m 1 g T Modern Fizikte IplerRolativistik teorideki ip benzeri objeler mesela modern ip teorisinde kullanilan veya kuarklar arasindaki etkilesim modellerinde kullanilan ipler gibi gerilmeye sahiptirler Enerji ip uzunluguyla orantilidir Sonuc olarak bu tip iplerde gerilme uzama miktarindan bagimsizdir Uzayabilen iplerde Hooke Yasasi uygulanir Kaynakca a b c d Giancoli Douglas C 2008 Section 5 7 Physics for Scientists and Engineers with Modern Physics 7 bas Pearson Education ISBN 9780131495081 20 Agustos 2020 tarihinde kaynagindan Erisim tarihi 27 Aralik 2020 Fetter Alexander L Walecka John Dirk 2003 Theoretical Mechanics of Particles and Continua Dover Books on Physics Courier Corporation ISBN 9780486432618 19 Agustos 2020 tarihinde kaynagindan Erisim tarihi 27 Aralik 2020
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans



