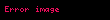Elektromanyetizma fiziğinde, Abraham-Lorentz kuvveti (ayrıca Lorentz-Abraham kuvveti) elektromanyetik radyasyon yayması nedeniyle hızlanan yüklü bir parçacıktaki geri tepme kuvvet idir. Ayrıca radyasyon reaksiyon kuvveti veya kendinden kuvvet denir. Formül özel görelilik teorisini önceler ve ışık hızı düzeninin hızlarında geçerli değildir. Bunun göreli genellemesine "Abraham-Lorentz-Dirac kuvveti" denir. Bunların her ikisi de kuantum fiziği değil, klasik fizik 'in bilgi kapsamındadır. Bu nedenle yaklaşık olarak Compton dalga boyu veya altındaki mesafelerde geçerli olmayabilir. Ancak tamamıyla kuantum ve göreli olan benzer bir formül vardır, bu formül "Abraham-Lorentz-Dirac-Langevin denklemi" olarak adlandırılır.
Kuvvet, nesnenin yük ünün karesinin ivmenin zamana göre değişiminin (sarsım, İngilizce: ) çarpımıyla orantılıdır. Kuvvet sarsım yönündedir. Örneğin, sarsımın hız ile zıt yönde olduğu bir siklotronda, radyasyon reaksiyonu, frenleme eylemi sağlayan parçacığın hızı ile zıt yöndedir.
Abraham-Lorentz kuvveti probleminin çözümünün, gelecekten sinyallerin şu anı etkilediği kehanetinde bulunduğu ve dolayısıyla neden-sonuç ilkesinin önsezisine meydan okuduğu düşünülüyordu. Örneğin, bir taneciğin kuvvet uygulanmadan önce hızlandığını öngören Abharam-Lorentz-Dirac denklemini kullanan patolojik çözümler vardır. Bu çözümler ön hızlanma çözümleri olarak da adlandırılır. Bu problemin bir çözümü Yaghjian, Rohrlich ve Medina tarafından tartışılmıştır.
Tanım ve açıklama
Matematiksel olarak Abraham-Lorentz kuvveti uluslararası ölçü biriminde (İngilizce: )
veya Gauss ölçü biriminde (İngilizce’de )
Burada Frad kuvet, 
Bu formülün göreli olmayan hızlar için olduğunu unutmayınız; Dirac sadece göreli uyarlamasını bulmak için, hareket denklemindeki parçacığın kütlesini yeniden normalize etmiştir.
Fiziksel olarak, hızlanan bir yük, bu yükten uzakta momentum taşıyan radyasyonu yayar. (Larmor formülü ne göre). Momentum korunduğundan, yük, yayılan radyasyon yönüne ters yönde itilir. Aşağıda gösterildiği gibi, aslında radyasyon kuvveti için yukarıdaki formül Larmor formülünden elde edilebilir.
Arka plan
Klasik elektrodinamikte problemler genel olarak iki sınıfa ayrılır:
- Yükün ve geçerli alan kaynaklarının belirlendiği ve bu alanların hesaplandığı problemler ve
- Tersine, alanların belirlendiği ve parçacığın hareketinin hesaplandığı problemler
Fiziğin bazı alanlarında; örneğin plazma fiziği ve taşıma katsayılarının (iletkenlik, difüzyon vs.) hesaplanmasında, kaynaklar tarafından oluşturulan alanlar ve kaynakların hareketi istikrarlı bir şekilde çözülür. Fakat bu gibi durumlarda, seçili kaynağın hareketi diğer tüm kaynaklar tarafından oluşturulan alanlara karşılık olarak hesaplanır. Parçacığın (kaynak) hareketinin aynı parçacık tarafından oluşturulan alanların sayesinde hesaplandığı nadirdir. Bunun nedeni iki yönlüdür:
- ın ihmal edilmesi genellikle birçok uygulama için yeterli doğrulukta cevaplara yol açar ve
- Kendinden oluşumlu alanların dahil edilmesi fizikte, gibi bazıları hala çözülememiş problemlere yol açar. Bu madde ve enerjinin doğası ile ilgilidir.
Kendinden oluşumlu alanlar tarafından meydana gelen bu kavramsal problemler, standart lisans metninde vurgulanmaktadır. [Jackson]
Bu problemin sunduğu zorluklar fiziğin en temel yönlerinden birine, temel parçacığın doğasına dokunmaktadır. Sınırlı alanlarda uygulanabilir kısmi çözümlerin verilebilmesine rağmen, temel problem çözümsüz kalmaktadır. Klasik yaklaşımlardan, kuantum mekaniksel yaklaşımlara geçiş zorlukları ortadan kaldırabileceği düşünülmekteydi. Bir yandan hala nihayetinde meydana gelebilecek bir umut varken, kuantum mekaniksel tartışmalar, klasik tartışmalardan bile daha ayrıntılı problemler ile kuşanmıştır. Kuantum elektrodinamiğindeki bu zorlukları önlemek için Lorent kovaryansı ve Lorentz değişmezliği kavramlarının akıllıca kullanılması ve bu sayede deneyle tam bir mutabakat içinde, son derecede yüksek hassasiyetteki çok küçük ışınımsal etkilerin hesaplanmasına olanak tanınması son yıllara (~1948–1950) nispeten önemli başarılardan biridir. Ancak temel bakış açısıyla problemler sürmektedir.
Abraham-Lorentz kuvveti kendinden oluşumlu alanların etkilerinin en temel hesaplanışının sonucudur. Hızlanan yüklerin radyasyon yaymasının gözlemlenmesinden ortaya çıkmıştır. Kuantum etkileri nin başlangıcı, kuantum elektrodinamiği ne yol açar. Kuantum elektrodinamiğindeki kendinden oluşumlu alanlar, hesaplamalarda sonlu sayıda renormalizasyon işlemiyle ortadan kaldırılabilen sonsuzluklar üretir. Bu, teorinin, insanların bugüne kadar yaptığı en doğru tahminleri yapabilmesine olanak tanıdı. Bakınız . Ancak renormalizasyon işlemi yerçekimi kuvvetine uygulandığında başarısız olur. Bu durumda sonsuzluklar sonsuz sayıdadır, bu da renormalizasyonun başarısızlığına sebep olur. Bu yüzden genel göreliliğin çözülemeyen bir problemi vardır. Sicim kuramı ve kuantum çekim döngüsü veya olarak adlandırılan bu problemi çözme girişimindedir.
Türetilişi
Kendinden kuvvet için en basit türevleniş; periyodik harekette, noktasal yükün radyasyonu için olan Larmor denkleminden bulunur:
Eğer yüklü parçacığın hareketinin periyodik olduğunu varsayarsak, Abraham-Lorentz kuvvetinin parçacık üzerinde yaptığı ortalama iş, Larmor gücünün 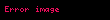
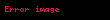
.
Yukarıdaki ifadenin integralini kısımlara bölerek alabiliriz. Eger periyodik hareket olduğunu varsayarsak, parçalı integraldeki sınır terimleri yok olur:
.
Açık bir şekilde aşağıdaki gibi tanımlayabiliriz:
.
Periyodik hareket gerektirmeyen daha kesin bir türevleniş Alan Kuramı formülasyonu kullanılarak bulunmuştur. Tamamıyla göreli ifadeler bulunan bir başka alternatif türevleniş de Dirac tarafından bulunmuştur.
Gelecekten sinyaller
Aşağıdaki, klasik bir analizin nasıl şaşırtıcı sonuçlara yol açabileceğinin bir örneklemesidir. Klasik teori nedensellik ilkesine karşı gibi görünebilir ve dolasıyla teorinin hem çökme sinyalleri verdiği hem de genişletilmeye ihtiyacı olduğu düşünülebilir. Bu durumda genişleme kuantum mekaniği ve göreli karşılığı kuantum alan teorisi dir. Rohrlich’in in the introduction concerning "fiziksel bir teorinin geçerli sınırlarına uymanın önemi" ile ilgili girişindeki alıntıya bakınız.
Harici kuvvet (İngilizce: external force 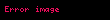
eşitliğine sahibiz. Burada :
Bu eşitliği bir kez integrallersek:
Bu integral şu andan gelecekteki sonsuzluğa kadar uzar. Bu yüzden kuvvetin gelecek değerleri, parçacığın şu anki ivmesini etkiler. Gelecek değerleri, gelecekteki 
faktörüyle ölçülebilir. Bu yüzden gelecekteki yaklaşık olarak bir 

Abraham–Lorentz–Dirac Kuvveti
Dirac göreli genellemeyi bulmak için 1938’de, denklemdeki Abraham-Lorentz kuvvetiyle hareket eden kütleyi yeniden normalize etti. Bu normalize edilen hareket denklemi Abraham–Lorentz–Dirac hareket denklemi olarak adlandırılır.
Tanım
Dirac tarafından elde edilen bu ifade (−, +, +, +) işaretlerinde,
şeklinde verilir. Liénard'ın deki Larmor formülünden elde ettiği
ile, güç aşağıdaki gibidir.
Paradokslar
Göreli olmayan durumla benzer olarak, harici kuvvette değişim bekleyen ve buna göre bir taneciğin bir kuvvetin uygulanmasından önce hızlandığını öngören Abraham-Lorentz-Dirac denklemini kullanan, ön hızlanma çözümleri olarak da adlandırılan patolojik çözümler vardır. Bu problemin bir çözümü Yaghjian, Rohrlich ve Medina tarafından tartışılmıştır.
Kaynakça
- ^ Yaghjian, Arthur D. (2006). Relativistic Dynamics of a Charged Sphere: Updating the Lorentz–Abraham Model. Lecture Notes in Physics. 686 (2 bas.). New York: Springer. Chapter 8. ISBN .
- ^ Rodrigo Medina (2006). "Radiation reaction of a classical quasi-rigid extended particle". Journal of Physics A: Mathematical and General. 39 (14). ss. 3801-3816. arXiv:physics/0508031 $2. Bibcode:2006JPhA...39.3801M. doi:10.1088/0305-4470/39/14/021.
- ^ F. Rohrlich: The dynamics of a charged sphere and the electron Am J Phys 65 (11) p. 1051 (1997) 22 Şubat 2014 tarihinde Wayback Machine sitesinde .. "The dynamics of point charges is an excellent example of the importance of obeying the validity limits of a physical theory. When these limits are exceeded the predictions of the theory may be incorrect or even patently absurd. In the present case, the classical equations of motion have their validity limits where quantum mechanics becomes important: they can no longer be trusted at distances of the order of (or below) the Compton wavelength… Only when all distances involved are in the classical domain is classical dynamics acceptable for electrons."
Konuyla ilgili yayınlar
- Griffiths, David J. (1998). Introduction to Electrodynamics (3.3 yayıncı=Prentice Hall bas.). ISBN . See sections 11.2.2 and 11.2.3
- Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN .\
- Donald H. Menzel, Fundamental Formulas of Physics, 1960, Dover Publications Inc., , vol. 1, page 345.
Dış bağlantılar
- MathPages – Does A Uniformly Accelerating Charge Radiate?4 Mart 2016 tarihinde Wayback Machine sitesinde .
- Feynman: The Development of the Space-Time View of Quantum Electrodynamics12 Mayıs 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Elektromanyetizma fiziginde Abraham Lorentz kuvveti ayrica Lorentz Abraham kuvveti elektromanyetik radyasyon yaymasi nedeniyle hizlanan yuklu bir parcaciktaki geri tepme kuvvet idir Ayrica radyasyon reaksiyon kuvveti veya kendinden kuvvet denir Formul ozel gorelilik teorisini onceler ve isik hizi duzeninin hizlarinda gecerli degildir Bunun goreli genellemesine Abraham Lorentz Dirac kuvveti denir Bunlarin her ikisi de kuantum fizigi degil klasik fizik in bilgi kapsamindadir Bu nedenle yaklasik olarak Compton dalga boyu veya altindaki mesafelerde gecerli olmayabilir Ancak tamamiyla kuantum ve goreli olan benzer bir formul vardir bu formul Abraham Lorentz Dirac Langevin denklemi olarak adlandirilir Kuvvet nesnenin yuk unun karesinin ivmenin zamana gore degisiminin sarsim Ingilizce carpimiyla orantilidir Kuvvet sarsim yonundedir Ornegin sarsimin hiz ile zit yonde oldugu bir siklotronda radyasyon reaksiyonu frenleme eylemi saglayan parcacigin hizi ile zit yondedir Abraham Lorentz kuvveti probleminin cozumunun gelecekten sinyallerin su ani etkiledigi kehanetinde bulundugu ve dolayisiyla neden sonuc ilkesinin onsezisine meydan okudugu dusunuluyordu Ornegin bir tanecigin kuvvet uygulanmadan once hizlandigini ongoren Abharam Lorentz Dirac denklemini kullanan patolojik cozumler vardir Bu cozumler on hizlanma cozumleri olarak da adlandirilir Bu problemin bir cozumu Yaghjian Rohrlich ve Medina tarafindan tartisilmistir Tanim ve aciklamaMatematiksel olarak Abraham Lorentz kuvveti uluslararasi olcu biriminde Ingilizce Frad m0q26pca q26pϵ0c3a displaystyle mathbf F mathrm rad frac mu 0 q 2 6 pi c mathbf dot a frac q 2 6 pi epsilon 0 c 3 mathbf dot a veya Gauss olcu biriminde Ingilizce de Frad 23q2c3a displaystyle mathbf F mathrm rad 2 over 3 frac q 2 c 3 mathbf dot a Burada Frad kuvet a displaystyle mathbf dot a salinim ivme nin turevi veya yerdegistirme nin ucuncu turevi m0 e0 c daki isik hizi ve q parcacigin elektrik yuku dur Bu formulun goreli olmayan hizlar icin oldugunu unutmayiniz Dirac sadece goreli uyarlamasini bulmak icin hareket denklemindeki parcacigin kutlesini yeniden normalize etmistir Fiziksel olarak hizlanan bir yuk bu yukten uzakta momentum tasiyan radyasyonu yayar Larmor formulu ne gore Momentum korundugundan yuk yayilan radyasyon yonune ters yonde itilir Asagida gosterildigi gibi aslinda radyasyon kuvveti icin yukaridaki formul Larmor formulunden elde edilebilir Arka planKlasik elektrodinamikte problemler genel olarak iki sinifa ayrilir Yukun ve gecerli alan kaynaklarinin belirlendigi ve bu alanlarin hesaplandigi problemler ve Tersine alanlarin belirlendigi ve parcacigin hareketinin hesaplandigi problemler Fizigin bazi alanlarinda ornegin plazma fizigi ve tasima katsayilarinin iletkenlik difuzyon vs hesaplanmasinda kaynaklar tarafindan olusturulan alanlar ve kaynaklarin hareketi istikrarli bir sekilde cozulur Fakat bu gibi durumlarda secili kaynagin hareketi diger tum kaynaklar tarafindan olusturulan alanlara karsilik olarak hesaplanir Parcacigin kaynak hareketinin ayni parcacik tarafindan olusturulan alanlarin sayesinde hesaplandigi nadirdir Bunun nedeni iki yonludur in ihmal edilmesi genellikle bircok uygulama icin yeterli dogrulukta cevaplara yol acar ve Kendinden olusumlu alanlarin dahil edilmesi fizikte gibi bazilari hala cozulememis problemlere yol acar Bu madde ve enerjinin dogasi ile ilgilidir Kendinden olusumlu alanlar tarafindan meydana gelen bu kavramsal problemler standart lisans metninde vurgulanmaktadir Jackson Bu problemin sundugu zorluklar fizigin en temel yonlerinden birine temel parcacigin dogasina dokunmaktadir Sinirli alanlarda uygulanabilir kismi cozumlerin verilebilmesine ragmen temel problem cozumsuz kalmaktadir Klasik yaklasimlardan kuantum mekaniksel yaklasimlara gecis zorluklari ortadan kaldirabilecegi dusunulmekteydi Bir yandan hala nihayetinde meydana gelebilecek bir umut varken kuantum mekaniksel tartismalar klasik tartismalardan bile daha ayrintili problemler ile kusanmistir Kuantum elektrodinamigindeki bu zorluklari onlemek icin Lorent kovaryansi ve Lorentz degismezligi kavramlarinin akillica kullanilmasi ve bu sayede deneyle tam bir mutabakat icinde son derecede yuksek hassasiyetteki cok kucuk isinimsal etkilerin hesaplanmasina olanak taninmasi son yillara 1948 1950 nispeten onemli basarilardan biridir Ancak temel bakis acisiyla problemler surmektedir Abraham Lorentz kuvveti kendinden olusumlu alanlarin etkilerinin en temel hesaplanisinin sonucudur Hizlanan yuklerin radyasyon yaymasinin gozlemlenmesinden ortaya cikmistir Kuantum etkileri nin baslangici kuantum elektrodinamigi ne yol acar Kuantum elektrodinamigindeki kendinden olusumlu alanlar hesaplamalarda sonlu sayida renormalizasyon islemiyle ortadan kaldirilabilen sonsuzluklar uretir Bu teorinin insanlarin bugune kadar yaptigi en dogru tahminleri yapabilmesine olanak tanidi Bakiniz Ancak renormalizasyon islemi yercekimi kuvvetine uygulandiginda basarisiz olur Bu durumda sonsuzluklar sonsuz sayidadir bu da renormalizasyonun basarisizligina sebep olur Bu yuzden genel goreliligin cozulemeyen bir problemi vardir Sicim kurami ve kuantum cekim dongusu veya olarak adlandirilan bu problemi cozme girisimindedir TuretilisiKendinden kuvvet icin en basit turevlenis periyodik harekette noktasal yukun radyasyonu icin olan Larmor denkleminden bulunur P m0q26pca2 displaystyle P frac mu 0 q 2 6 pi c mathbf a 2 Eger yuklu parcacigin hareketinin periyodik oldugunu varsayarsak Abraham Lorentz kuvvetinin parcacik uzerinde yaptigi ortalama is Larmor gucunun t1 displaystyle tau 1 ve t2 displaystyle tau 2 araligindaki bir periyot integralinin negatif isaretlisine esittir t1t2Frad vdt t1t2 Pdt t1t2m0q26pca2dt t1t2m0q26pcdvdt dvdtdt displaystyle int tau 1 tau 2 mathbf F mathrm rad cdot mathbf v dt int tau 1 tau 2 Pdt int tau 1 tau 2 frac mu 0 q 2 6 pi c mathbf a 2 dt int tau 1 tau 2 frac mu 0 q 2 6 pi c frac d mathbf v dt cdot frac d mathbf v dt dt Yukaridaki ifadenin integralini kisimlara bolerek alabiliriz Eger periyodik hareket oldugunu varsayarsak parcali integraldeki sinir terimleri yok olur t1t2Frad vdt m0q26pcdvdt v t1t2 t1t2m0q26pcd2vdt2 vdt 0 t1t2m0q26pca vdt displaystyle int tau 1 tau 2 mathbf F mathrm rad cdot mathbf v dt frac mu 0 q 2 6 pi c frac d mathbf v dt cdot mathbf v bigg tau 1 tau 2 int tau 1 tau 2 frac mu 0 q 2 6 pi c frac d 2 mathbf v dt 2 cdot mathbf v dt 0 int tau 1 tau 2 frac mu 0 q 2 6 pi c mathbf dot a cdot mathbf v dt Acik bir sekilde asagidaki gibi tanimlayabiliriz Frad m0q26pca displaystyle mathbf F mathrm rad frac mu 0 q 2 6 pi c mathbf dot a Periyodik hareket gerektirmeyen daha kesin bir turevlenis Alan Kurami formulasyonu kullanilarak bulunmustur Tamamiyla goreli ifadeler bulunan bir baska alternatif turevlenis de Dirac tarafindan bulunmustur Gelecekten sinyallerAsagidaki klasik bir analizin nasil sasirtici sonuclara yol acabileceginin bir orneklemesidir Klasik teori nedensellik ilkesine karsi gibi gorunebilir ve dolasiyla teorinin hem cokme sinyalleri verdigi hem de genisletilmeye ihtiyaci oldugu dusunulebilir Bu durumda genisleme kuantum mekanigi ve goreli karsiligi kuantum alan teorisi dir Rohrlich in in the introduction concerning fiziksel bir teorinin gecerli sinirlarina uymanin onemi ile ilgili girisindeki alintiya bakiniz Harici kuvvet Ingilizce external force Fext displaystyle mathbf F mathrm ext etkisindeki bir parcacik icin mv Frad Fext mt0v Fext displaystyle m dot mathbf v mathbf F mathrm rad mathbf F mathrm ext mt 0 ddot mathbf v mathbf F mathrm ext esitligine sahibiz Burada t0 m0q26pmc displaystyle t 0 frac mu 0 q 2 6 pi mc Bu esitligi bir kez integrallersek mv 1t0 t exp t tt0 Fext t dt displaystyle m dot mathbf v 1 over t 0 int t infty exp left t t over t 0 right mathbf F mathrm ext t dt Bu integral su andan gelecekteki sonsuzluga kadar uzar Bu yuzden kuvvetin gelecek degerleri parcacigin su anki ivmesini etkiler Gelecek degerleri gelecekteki t0 displaystyle t 0 dan 4 kat buyuk bir hizla azalan exp t tt0 displaystyle exp left t t over t 0 right faktoruyle olculebilir Bu yuzden gelecekteki yaklasik olarak bir t0 displaystyle t 0 zaman araligindan gelen sinyaller su andaki ivmeyi etkiler Bir elektron icin bu zaman yaklasik olarak 10 24 displaystyle 10 24 saniyedir Bu sure bir isik dalgasinin bir elektronun buyuklugu boyunca yol almasi icin gecen sureye esittir Abraham Lorentz Dirac KuvvetiDirac goreli genellemeyi bulmak icin 1938 de denklemdeki Abraham Lorentz kuvvetiyle hareket eden kutleyi yeniden normalize etti Bu normalize edilen hareket denklemi Abraham Lorentz Dirac hareket denklemi olarak adlandirilir Tanim Dirac tarafindan elde edilen bu ifade isaretlerinde Fmrad moq26pmc d2pmdt2 pmm2c2 dpndtdpndt displaystyle F mu mathrm rad frac mu o q 2 6 pi mc left frac d 2 p mu d tau 2 frac p mu m 2 c 2 left frac dp nu d tau frac dp nu d tau right right seklinde verilir Lienard in deki Larmor formulunden elde ettigi P moq2a2g66pc displaystyle P frac mu o q 2 a 2 gamma 6 6 pi c ile guc asagidaki gibidir 1Dt 0tPdt 1Dt 0tF vdt displaystyle frac 1 Delta t int 0 t Pdt frac 1 Delta t int 0 t textbf F cdot textbf v dt Paradokslar Goreli olmayan durumla benzer olarak harici kuvvette degisim bekleyen ve buna gore bir tanecigin bir kuvvetin uygulanmasindan once hizlandigini ongoren Abraham Lorentz Dirac denklemini kullanan on hizlanma cozumleri olarak da adlandirilan patolojik cozumler vardir Bu problemin bir cozumu Yaghjian Rohrlich ve Medina tarafindan tartisilmistir Kaynakca Yaghjian Arthur D 2006 Relativistic Dynamics of a Charged Sphere Updating the Lorentz Abraham Model Lecture Notes in Physics 686 2 bas New York Springer Chapter 8 ISBN 978 0 387 26021 1 Rodrigo Medina 2006 Radiation reaction of a classical quasi rigid extended particle Journal of Physics A Mathematical and General 39 14 ss 3801 3816 arXiv physics 0508031 2 Bibcode 2006JPhA 39 3801M doi 10 1088 0305 4470 39 14 021 F Rohrlich The dynamics of a charged sphere and the electron Am J Phys 65 11 p 1051 1997 22 Subat 2014 tarihinde Wayback Machine sitesinde The dynamics of point charges is an excellent example of the importance of obeying the validity limits of a physical theory When these limits are exceeded the predictions of the theory may be incorrect or even patently absurd In the present case the classical equations of motion have their validity limits where quantum mechanics becomes important they can no longer be trusted at distances of the order of or below the Compton wavelength Only when all distances involved are in the classical domain is classical dynamics acceptable for electrons Konuyla ilgili yayinlarGriffiths David J 1998 Introduction to Electrodynamics 3 3 yayinci Prentice Hall bas ISBN 0 13 805326 X See sections 11 2 2 and 11 2 3 Jackson John D 1998 Classical Electrodynamics 3rd ed Wiley ISBN 0 471 30932 X Donald H Menzel Fundamental Formulas of Physics 1960 Dover Publications Inc ISBN 0 486 60595 7 vol 1 page 345 Dis baglantilarMathPages Does A Uniformly Accelerating Charge Radiate 4 Mart 2016 tarihinde Wayback Machine sitesinde Feynman The Development of the Space Time View of Quantum Electrodynamics12 Mayis 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State