Bu madde tümüyle ya da çoğunluğuyla dayanıyor. (Ağustos 2020) |
Bilgisayar bilimlerinde, alt küme toplamı problemi karmaşıklık kuramında ve kriptografide önemli yeri olan bir problemdir.
Karmaşıklık kuramında, problemin tanımı ve açıklaması basit ve anlaşılır olduğundan NP-Complete sınıfında yer alan problemleri anlayabilmek için iyi bir örnek oluşturmaktadır.
Kriptografide ise, alt küme toplamı probleminin önemli bir yer tutmasının sebebi, şifrelenmiş bir metnin anahtarını bulabilmeyi sağlamasıdır.
Problemin Tanımı
Alt küme toplamı sınıfı, alt kümeleri arasında elemanları toplamı t olan bir küme bulunan tüm S kümelerini içerir. Matematiksel olarak şöyle ifade edilir:
SUBSET-SUM = { < S,t > | S = {
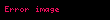
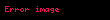
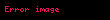
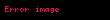
Bu tanımda geçen S ve Y kümeleri multisetlerdir, bu kümelerde eleman tekrarına izin verilir.
Basit bir örnek vermek gerekirse: < {1,2,3,4}, 5 > ∈ SUBSET-SUM
Alt Küme Toplamı Probleminin Karmaşıklığı
Alt küme toplamı problemi NP-Complete sınıfında yer almaktadır. Bir dilin NP-Complete sınıfına ait olduğunu göstermek için;
- Dilin, NP sınıfında yer aldığını,
- NP sınıfında yer alan diğer tüm dillerin polinom zamanda o dile indirgenebilir olduğunu
göstermek gerekmektedir.
Alt Küme Toplamı Problemi NP Sınıfında Bulunur
Alt küme toplamı probleminin [NP] sınıfında yer aldığını, 
V= "< < S,t >,c > girdisinde:
- Sertifikada bulunan elemanların toplamının t’ye eşit olup olmadığını test et
- Sertifikada bulunan elemanların S kümesinin elemanı olup olmadığını test et
- Eğer ikisi de tamamsa, kabul et; değilse reddet."
3SAT Problemi, Alt Küme Toplamı Problemine Polinom Zamanda İndirgenebilir
NP sınıfındaki tüm dillerin polinom zamanda alt küme toplamı diline indirgenebilir olduğunu göstermek için NP-Complete olan 3SAT dili kullanılabilir.
Bu problemin alt küme toplamı problemine polinom zamanda indirgenebilir, 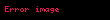
Φ; 
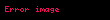
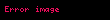
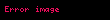
Kullanılacak olan tabloda kolonlar, Φ formülünün değişkenlerini ve cümlelerini; satırlar ise, S kümesinin elemanlarının ve t toplamının ondalık düzende gösterimlerini ifade eder.
Tablodaki çift çizginin üzerinde bulunan 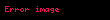
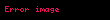
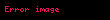
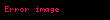
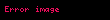
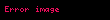
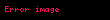
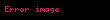

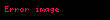
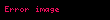
- Eğer
∈
ise
sayısının j’inci hanesine 1 konur.
- Eğer
i ∈
ise
sayısının j’inci hanesine 1 konur.
Değerinin 1 olduğu belirtilmemiş hanelere ise 0 rakamı yerleştirilir.
Yukarıda bahsedilenlere ek olarak S kümesi, Φ’de bulunan her bir cümle için g ve h sayılarını barındırır. Bu iki sayı birbirine eşittir. Bu sayılar, 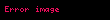
Aşağıdaki tablo Φ = ( 

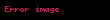


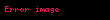




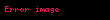
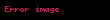



- Φ'nin doğrulanabilir (satisfiable) olduğu varsayılırsa;
Bu varsayıma göre S’in bir alt kümesi oluşturulabilir. Bu alt kümeyi oluşturmak için şöyle bir yol izlenebilir:
- Φ’yi doğrulayan
değişkeninin değeri TRUE ise altkümeye
sayısı
- Φ’yi doğrulayan
değişkeninin değeri FALSE ise altkümeye
sayısı
seçilir.
Oluşturulan bu alt kümenin elemanları toplandığında, tablonun t satırındaki ilk l hanede 1 rakamı elde edilir, çünkü alt kümeye ya 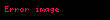
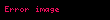
- S kümesinin elemanları toplamı t olan bir alt kümesi olduğu varsayılırsa;
Tablodan da görüldüğü gibi, altküme elemanlarının hanelerinde ya 1 ya da 0 rakamı bulunmaktadır, ayrıca her kolonda en fazla 5 adet 1 rakamı bulunduğundan toplama işlemi eldesiz gerçekleşir. İlk l kolonda toplamın 1 olması, ya 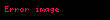
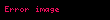
- Eğer alt kümede
sayısı bulunuyorsa
değişkenine TRUE değeri,
- Eğer alt kümede
sayısı bulunuyorsa
değişkenine FALSE değeri
atanır.
Bu atamayla Φ formülünün doğrulanabilirliği sağlanabilir, çünkü son satırdaki t sayısının son k hanesinde 3 rakamı bulunmaktadır. Son k kolonda toplamın 3 olmasını sağlayacak en az 1 tane değer, alt kümeye seçilmiş olan 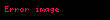
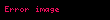
Bu durumda;
- eğer bu 1 rakamı,
sayısından geliyorsa
∈
ve
= TRUE
- eğer bu 1 rakamı,
sayısından geliyorsa
i ∈
ve
= FALSE
olduğundan dolayı Φ formülünde bulunan her 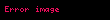
Son olarak da yukarıda bahsedilen tablonun kullanımıyla yapılan bu indirgemenin polinom zamanda gerçekleştirildiğini göstermek için tablonun boyutlarına bakılabilir. Tablonun boyutları kabaca 
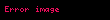
Ayrıca bakınız
Kaynakça
- ^ Michael Sipser: "Introduction to the Theory of Computation" Course Technology Press Second Edition, 2005.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde tumuyle ya da cogunluguyla tek kaynaga dayaniyor Lutfen baska kaynaklar ekleyerek bu maddeyi gelistirmeye yardim ediniz Agustos 2020 Bilgisayar bilimlerinde alt kume toplami problemi karmasiklik kuraminda ve kriptografide onemli yeri olan bir problemdir Karmasiklik kuraminda problemin tanimi ve aciklamasi basit ve anlasilir oldugundan NP Complete sinifinda yer alan problemleri anlayabilmek icin iyi bir ornek olusturmaktadir Kriptografide ise alt kume toplami probleminin onemli bir yer tutmasinin sebebi sifrelenmis bir metnin anahtarini bulabilmeyi saglamasidir Problemin TanimiAlt kume toplami sinifi alt kumeleri arasinda elemanlari toplami t olan bir kume bulunan tum S kumelerini icerir Matematiksel olarak soyle ifade edilir SUBSET SUM lt S t gt S x1 displaystyle x 1 xk displaystyle x k ve bazi Y y1 displaystyle y 1 yl displaystyle y l S icin i 1lyi t displaystyle sum i 1 l y i t Bu tanimda gecen S ve Y kumeleri multisetlerdir bu kumelerde eleman tekrarina izin verilir Basit bir ornek vermek gerekirse lt 1 2 3 4 5 gt SUBSET SUMAlt Kume Toplami Probleminin KarmasikligiAlt kume toplami problemi NP Complete sinifinda yer almaktadir Bir dilin NP Complete sinifina ait oldugunu gostermek icin Dilin NP sinifinda yer aldigini NP sinifinda yer alan diger tum dillerin polinom zamanda o dile indirgenebilir oldugunu gostermek gerekmektedir Alt Kume Toplami Problemi NP Sinifinda Bulunur Alt kume toplami probleminin NP sinifinda yer aldigini SUBSET SUM NP displaystyle SUBSET SUM in NP gostermek icin bir dogrulayici verifier kullanilabilir Sertifika olarak S in bir alt kumesini kullanacak olan bu dogrulayici asagidaki gibi yazilabilir V lt lt S t gt c gt girdisinde Sertifikada bulunan elemanlarin toplaminin t ye esit olup olmadigini test et Sertifikada bulunan elemanlarin S kumesinin elemani olup olmadigini test et Eger ikisi de tamamsa kabul et degilse reddet 3SAT Problemi Alt Kume Toplami Problemine Polinom Zamanda Indirgenebilir NP sinifindaki tum dillerin polinom zamanda alt kume toplami diline indirgenebilir oldugunu gostermek icin NP Complete olan 3SAT dili kullanilabilir Bu problemin alt kume toplami problemine polinom zamanda indirgenebilir 3SAT pSUBSET SUM displaystyle 3SAT leq p SUBSET SUM oldugu bir tablo kullanilarak gosterilebilir F x1 displaystyle x 1 xl displaystyle x l degiskenli c1 displaystyle c 1 ck displaystyle c k cumleli clause Boolean bir formul olsun Kullanilacak olan tabloda kolonlar F formulunun degiskenlerini ve cumlelerini satirlar ise S kumesinin elemanlarinin ve t toplaminin ondalik duzende gosterimlerini ifade eder Tablodaki cift cizginin uzerinde bulunan y1 displaystyle y 1 z1 displaystyle z 1 yl displaystyle y l zl displaystyle z l ve g1 displaystyle g 1 h1 displaystyle h 1 gk displaystyle g k hk displaystyle h k sayilari S kumesinin elemanlaridir cizginin alt kisminda kalan kisimda ise t sayisi yer alir Kullanilan bu tabloda F formulunde bulunan her bir xi displaystyle x i degiskeni icin yi displaystyle y i ve zi displaystyle z i seklinde 2 sayi yer alir Bu sayilarin ondalik gosterimi iki bolumden olusur Tablonun sol tarafi degiskenin indisine uygun y ve z satirina 1 rakami geri kalan kisimlarina ise tabloda goruldugu gibi l i tane 0 yerlestirilerek olusturulur Tablonun sag tarafinda ise F de bulunan her bir cumle icin bir hane bulunur ve su sekilde doldurulur Eger xi displaystyle x i cj displaystyle c j ise yi displaystyle y i sayisinin j inci hanesine 1 konur Eger x displaystyle bar x i cj displaystyle c j ise zi displaystyle z i sayisinin j inci hanesine 1 konur Degerinin 1 oldugu belirtilmemis hanelere ise 0 rakami yerlestirilir Yukarida bahsedilenlere ek olarak S kumesi F de bulunan her bir cumle icin g ve h sayilarini barindirir Bu iki sayi birbirine esittir Bu sayilar cj displaystyle c j cumlesine uygun dusen haneye 1 rakami geri kalan k j haneye ise 0 yerlestirilerek olusturulur Asagidaki tablo F x1 displaystyle x 1 displaystyle lor x displaystyle bar x 2 displaystyle lor x3 displaystyle x 3 displaystyle land x2 displaystyle x 2 displaystyle lor x3 displaystyle x 3 displaystyle lor displaystyle land x displaystyle bar x 3 displaystyle lor displaystyle lor icin doldurulmustur F nin dogrulanabilir satisfiable oldugu varsayilirsa dd Bu varsayima gore S in bir alt kumesi olusturulabilir Bu alt kumeyi olusturmak icin soyle bir yol izlenebilir F yi dogrulayan xi displaystyle x i degiskeninin degeri TRUE ise altkumeye yi displaystyle y i sayisi F yi dogrulayan xi displaystyle x i degiskeninin degeri FALSE ise altkumeye zi displaystyle z i sayisi secilir Olusturulan bu alt kumenin elemanlari toplandiginda tablonun t satirindaki ilk l hanede 1 rakami elde edilir cunku alt kumeye ya yi displaystyle y i ya da zi displaystyle z i sayisi secilmistir Ayrica son k hanede ise toplamin en fazla 3 en az 1 oldugu gorulur Bunun sebebi F formulu dogrulanabilir oldugundan her cumlede en fazla 3 en az 1 degiskenin TRUE degerini almis olmasidir Toplamin 3 olmadigi durumlarda ise uygun indisli g ve veya h sayilari kullanilarak toplamin 3 e ulasmasi saglanabilir S kumesinin elemanlari toplami t olan bir alt kumesi oldugu varsayilirsa dd Tablodan da goruldugu gibi altkume elemanlarinin hanelerinde ya 1 ya da 0 rakami bulunmaktadir ayrica her kolonda en fazla 5 adet 1 rakami bulundugundan toplama islemi eldesiz gerceklesir Ilk l kolonda toplamin 1 olmasi ya yi displaystyle y i sayisinin ya da zi displaystyle z i sayisinin alt kume elemanlari arasinda yer almakta oldugunu gosterir Ikisi birden alt kumede bulunamaz cunku o durumda toplamlari 2 olacagindan varsayima aykiri olur Bu varsayimdan yola cikilarak F formulunun dogrulanabilirligi su sekilde saglanabilir Eger alt kumede yi displaystyle y i sayisi bulunuyorsa xi displaystyle x i degiskenine TRUE degeri Eger alt kumede zi displaystyle z i sayisi bulunuyorsa xi displaystyle x i degiskenine FALSE degeri atanir Bu atamayla F formulunun dogrulanabilirligi saglanabilir cunku son satirdaki t sayisinin son k hanesinde 3 rakami bulunmaktadir Son k kolonda toplamin 3 olmasini saglayacak en az 1 tane deger alt kumeye secilmis olan yi displaystyle y i veya zi displaystyle z i sayisindan gelmelidir cunku alt kumeye secilebilecek olan g ve h sayilarindan en fazla 2 toplami elde edilebilir Bu durumda eger bu 1 rakami yi displaystyle y i sayisindan geliyorsa xi displaystyle x i cj displaystyle c j ve xi displaystyle x i TRUE eger bu 1 rakami zi displaystyle z i sayisindan geliyorsa x displaystyle bar x i cj displaystyle c j ve xi displaystyle x i FALSE oldugundan dolayi F formulunde bulunan her cj displaystyle c j cumlesi dogrulanabilir dolayisiyla F formulu dogrulanabilir oldugu gosterilebilir Son olarak da yukarida bahsedilen tablonun kullanimiyla yapilan bu indirgemenin polinom zamanda gerceklestirildigini gostermek icin tablonun boyutlarina bakilabilir Tablonun boyutlari kabaca k l 2 displaystyle k l 2 olarak ifade edilebilir dolayisiyla bu indirgeme icin harcanan zamanin O n2 displaystyle n 2 oldugu soylenebilir Ayrica bakinizCook Levin teoremi 3SAT KLIK indirgemesi Bagimsiz kume problemi Hamilton yolu problemi KarmasiklikKaynakca Michael Sipser Introduction to the Theory of Computation Course Technology Press Second Edition 2005
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans