Anderson-Darling sınaması, istatistik bilim dalında, bir parametrik olmayan istatistik sınaması olup örneklem verilerinin belirli bir olasılık dağılımı gösterip göstermediğini sınamak için, yani uygunluk iyiliği sınaması için, kullanılmaktadır. Bu sınama ilk defa 1952'de Amerikan istatistikçileri T.W.Anderson Jr. ile D.A.Darling tarafından yayınlanmıştır. Bu sınama Kolmogorov-Smirnov sınamasının değiştirilmesi ve olasılık dağılımının kuyruklarına daha çok ağırlık verilmesi ile ortaya çıkartılmıştır.
Anderson-Darling sınamasının pratikte veriler için normal dağılımdan ayrılıp ayrılmadığını incelemek için kullanılan normallik sınaması yöntemleri arasında bulunan en güçlü sınamalardan biri olduğu iddia edilmektedir. Hem çok küçük (n le; 25) örneklem sayılı veriler için hem de hacmi 200u aşan sanayi kalite kontrol verileri için başarıyla normallik sınaması için kullanıldığı bildirilmiştir.
Genel uygunluk iyiliği sınaması
Anderson-Darling sınaması bir örneklem verisinin tam olarak belirlenmiş bir olasılık dağılımı gösteren bir anakütleden gelip gelmediğinin sınanması için kullanılır. Verilmiş N büyüklük sayıda bir örneklem veri serisi, yani 
Anderson-Darling sınaması için sıfır hipotez, her türden uygunluk iyiliği sınaması gibi, örneklem verilerin için tüm parametre değerleri ile iyice belirlenen olasılık dağılımlı anakütleden geldiğidir. Bu sıfır hipotezin çok sınırlı olduğuna dikkat çekilmelidir. Ancak verilmiş parametre veya parametreler için olasılık dağılımı uygulanması incelenmektedir. Eğer sıfır hipotez sınama sonucu ret edilirse, verilerin parametre(ler) ile belirlenmiş dağılıma uymadığı sonucuna varılır. Tekrar edilmelidir ki genel olarak belli bir dağılım ret edilmemektedir; sadece belli parametresi olan dağılım ret edilmektedir.
Elde edilen veriler en küçük değerden en büyük değere kadar bir sıraya konulur. Bu sıraya konulmuş veriler, yani 

Bu toplam kullanılarak Anderson-Darling istatistiği 
elde edilir.
Sıfır hipotezde belirtilen olasılık dağılımına göre, elde edilen 


Bazı olasılık dağılımları için özel tablolar geliştirilmiş ve değişik parametre değerleri ve belirtilmiş anlamlılık değerleri için (genellikle %1 ve %5) kritik değerler tabloda belirtilmiştir. Normal dağılım, log-normal dağılım, üstel dağılım, Weibull dağılımı, logistik dağılım ve Tip I uçsal değerler için bu tabloların bulunduğu bilinmektedir. Tablodan bulunan kritik değer, hesaplanmış 
Normallik sınaması
Anderson-Darling sınamasının bir normallik sınaması olarak kullanılmasındaki genel mantıksal temel, veri serileri ile belirlenmiş normal dağılım arasında bir uzaklık ifade eden bulunmasıdır. Bu temel, hipotez olan dağılımın gerçekte bulunduğu kabul edilirse, veri serisinin bir tekdüze dağılıma dönüştürülebilineceği kavramına dayanır. Böylece dönüştürülen örneklem veri serisi bir uzaklık sınaması kullanılarak tekdüze dağılım olup olmadığı test edilir.
Veri serisi yani 
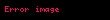


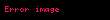



Bu dönüştürülmüş veriler hesaplamalar da kullanılır.
Örneklemden bulunan ortalama 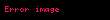


Standart normal dağılım için birikimli dağılım fonksiyonu 

veya tekrar eden indeksler yazılmazsa
Eğer herhangi bir 


Eğer 

Eğer 
Yapılan araştırmalara göre Anderson-Darling sınaması için sınama istatistiği olan 

İçsel kaynaklar
Kaynakça
- ^ Anderson Jr.,T.W. ve Darling,D.A. (1952) "Asymptotic theory of certain 'goodness-of-fit' criteria based on stochastic processes' Annals of Mathematical Statistics C.23 say. 193–212
- ^ Stephens,M.A. (1974) "EDF Statistics for Goodness of Fit and Some Comparisons" Journal of the American Statistical Association C.69 say.730–737
- ^ a b Stephens/
Dışsal kaynaklar
- [1]18 Mayıs 2008 tarihinde Wayback Machine sitesinde . US NIST İstatistik Elkitabı.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Anderson Darling sinamasi istatistik bilim dalinda bir parametrik olmayan istatistik sinamasi olup orneklem verilerinin belirli bir olasilik dagilimi gosterip gostermedigini sinamak icin yani uygunluk iyiligi sinamasi icin kullanilmaktadir Bu sinama ilk defa 1952 de Amerikan istatistikcileri T W Anderson Jr ile D A Darling tarafindan yayinlanmistir Bu sinama Kolmogorov Smirnov sinamasinin degistirilmesi ve olasilik dagiliminin kuyruklarina daha cok agirlik verilmesi ile ortaya cikartilmistir Anderson Darling sinamasinin pratikte veriler icin normal dagilimdan ayrilip ayrilmadigini incelemek icin kullanilan normallik sinamasi yontemleri arasinda bulunan en guclu sinamalardan biri oldugu iddia edilmektedir Hem cok kucuk n le 25 orneklem sayili veriler icin hem de hacmi 200u asan sanayi kalite kontrol verileri icin basariyla normallik sinamasi icin kullanildigi bildirilmistir Genel uygunluk iyiligi sinamasiAnderson Darling sinamasi bir orneklem verisinin tam olarak belirlenmis bir olasilik dagilimi gosteren bir anakutleden gelip gelmediginin sinanmasi icin kullanilir Verilmis N buyukluk sayida bir orneklem veri serisi yani X1 XN displaystyle X 1 cdots X N kullanilir Bu serinin sinanmansi icin hangi olasilik dagilimindan geldiginin ve bu olasilik dagilimini tam olarak belirleyen parametre degerinin veya parametreler degerlerinin verilmesi gerekir Anderson Darling sinamasi icin sifir hipotez her turden uygunluk iyiligi sinamasi gibi orneklem verilerin icin tum parametre degerleri ile iyice belirlenen olasilik dagilimli anakutleden geldigidir Bu sifir hipotezin cok sinirli olduguna dikkat cekilmelidir Ancak verilmis parametre veya parametreler icin olasilik dagilimi uygulanmasi incelenmektedir Eger sifir hipotez sinama sonucu ret edilirse verilerin parametre ler ile belirlenmis dagilima uymadigi sonucuna varilir Tekrar edilmelidir ki genel olarak belli bir dagilim ret edilmemektedir sadece belli parametresi olan dagilim ret edilmektedir Elde edilen veriler en kucuk degerden en buyuk degere kadar bir siraya konulur Bu siraya konulmus veriler yani Y1 lt lt YN displaystyle Y 1 lt cdots lt Y N bir sinama istatistiginin hesaplanmasi icin kullanilir Parametresi veya parametreleri verilmis olasilik dagilimi icin birikimli dagilim fonksiyonu kullanilarak bir sira F displaystyle F degerleri bulununur Bu iki seri kullanilarak once su S toplami elde edilir S k 1N2k 1N ln F Yk ln 1 F YN 1 k displaystyle S sum k 1 N frac 2k 1 N left ln F Y k ln left 1 F Y N 1 k right right Bu toplam kullanilarak Anderson Darling istatistigi A2 displaystyle A 2 degeri yani A2 N S displaystyle A 2 N S elde edilir Sifir hipotezde belirtilen olasilik dagilimina gore elde edilen A2 displaystyle A 2 degerinin belirli bir sabitle cok kere orneklem hacmi N e bagli olarak carpilmasi gerektir ve bu degistirilmis Anderson Darling istatistigi A 2 displaystyle A 2 adi altinda sinama istatistigi olarak kullanilir A 2 displaystyle A 2 sinama istatistigi belirlenen teorik olasilik dagilimi icin p degeri bulmak icin kullanilir Hesaplanmis p degeri eger 1 veya 5 olan anlamlilik seviyesinden buyuk ise sifir hipotez kabul edilir ve orneklem verisi belirlenen olasilik dagilimina uydugu sonucuna varilir Ancak bu p degeri bulma islemi bir olasilik dagilimi simulasyonu gerekecegi icin bilgisayarla sayisal hesaplama gerektirir Bazi olasilik dagilimlari icin ozel tablolar gelistirilmis ve degisik parametre degerleri ve belirtilmis anlamlilik degerleri icin genellikle 1 ve 5 kritik degerler tabloda belirtilmistir Normal dagilim log normal dagilim ustel dagilim Weibull dagilimi logistik dagilim ve Tip I ucsal degerler icin bu tablolarin bulundugu bilinmektedir Tablodan bulunan kritik deger hesaplanmis A 2 displaystyle A 2 degeri ile karsilastirilir Belirlenmis olasilik dagilimina uygunluk sifir hipotezinin kabul edilmesi sonucudur yani hesaplanmis deger tablo kritik degerinden buyukse orneklem verileri belirlenmis olasilik dagilimina uygunluk gosterir sonucuna varilir Normallik sinamasiAnderson Darling sinamasinin bir normallik sinamasi olarak kullanilmasindaki genel mantiksal temel veri serileri ile belirlenmis normal dagilim arasinda bir uzaklik ifade eden bulunmasidir Bu temel hipotez olan dagilimin gercekte bulundugu kabul edilirse veri serisinin bir tekduze dagilima donusturulebilinecegi kavramina dayanir Boylece donusturulen orneklem veri serisi bir uzaklik sinamasi kullanilarak tekduze dagilim olup olmadigi test edilir Veri serisi yani i 1 n displaystyle i 1 ldots n icin Xi displaystyle X i olarak verilmistir Ilk etapta bu seri en kucuk degerden en buyuk degere dogru siralanir yani X1 lt lt XN displaystyle X 1 lt cdots lt X N hesaplamalar icin kullanilir X displaystyle X icin ortalama X displaystyle bar X ve standart sapma s displaystyle s bulunur Sirali X displaystyle X soyle normalize edilerek Y displaystyle Y degiskenine donusturulur Yi Xi X s displaystyle Y i frac X i bar X s dd Bu donusturulmus veriler hesaplamalar da kullanilir Orneklemden bulunan ortalama X displaystyle bar X ve standart sapma s displaystyle s sifir hipoteze gore normal varsayilan anakutlenin parametrelerinin yansiz kestirimleri sayilir O zaman donusturulmus veriler kullanildigi icin sifir hipotez Y displaystyle Y nin dagiliminin standart normal dagilim yani N 0 1 oldugudur Standart normal dagilim icin birikimli dagilim fonksiyonu F displaystyle Phi olarak ifade edilirse Anderson Darling istatistigi yani A1 displaystyle A 1 soyle yazilir A2 n 1n i 1n 2i 1 ln F Yi ln 1 F Yn 1 i displaystyle A 2 n frac 1 n sum i 1 n 2i 1 ln Phi Y i ln 1 Phi Y n 1 i dd veya tekrar eden indeksler yazilmazsa A2 n 1n i 1n 2i 1 ln F Yi 2 n i 1 ln 1 F Yi displaystyle A 2 n frac 1 n sum i 1 n left 2i 1 ln Phi Y i 2 n i 1 ln 1 Phi Y i right dd Eger herhangi bir Pi 0veya1 displaystyle P i 0 quad veya quad 1 ise bu A2 displaystyle A 2 hesaplanamaz ve bu halde A2 displaystyle A 2 anlamsiz oldugu icin hesaplarin birakilmasi gerekir Eger A2 displaystyle A 2 hesaplanabilirse orneklem hacmi N ye icin yaklasik bir ayarlama yapilarak degistirilmis Anderson Darling istatistigi A 2 displaystyle A 2 olarak soyle bulunur A 2 A2 1 0 75n 2 25n2 displaystyle A 2 A 2 left 1 frac 0 75 n frac 2 25 n 2 right dd Eger A 2 displaystyle A 2 degeri 0 752 degerini asarsa 5 anlamlilik seviyesinde sifir hipotez olan normallik ret edilir Yapilan arastirmalara gore Anderson Darling sinamasi icin sinama istatistigi olan A 2 displaystyle A 2 nin normallik sinamasi icin kullanilan yontemlerden en guclu olanlardan biri oldugu bulunmustur Buna en yakin gucte yontemin icin bulunan W2 displaystyle W 2 oldugu da ayni yazida aciklanmistir Icsel kaynaklarNormallik sinamalari Kolmogorov Smirnov sinamasi Shapiro Wilk sinamasi Jarque Bera sinamasiKaynakca Anderson Jr T W ve Darling D A 1952 Asymptotic theory of certain goodness of fit criteria based on stochastic processes Annals of Mathematical Statistics C 23 say 193 212 Stephens M A 1974 EDF Statistics for Goodness of Fit and Some Comparisons Journal of the American Statistical Association C 69 say 730 737 a b Stephens Dissal kaynaklar 1 18 Mayis 2008 tarihinde Wayback Machine sitesinde US NIST Istatistik Elkitabi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State





