Atwood düzeneği ya da Atwood makinesi, 1784 yılında, İngiliz matematikçi tarafından, laboratuvarda kanunlarının deneyleri yapılırken icat edilmiştir. Atwood düzeneği, klasik mekanik prensiplerini göstermek adına kullanılan yaygın bir düzenektir.

İdeal bir Atwood düzeneği, m1 ve m2 kütleleri olmak üzere birbirlerine uzatılamayan kütlesiz bir ip ve yine kütlesiz bir makarayla bağlanmak üzere iki kısımdan oluşur.
- m1 = m2 olduğu zaman, kütleler ne olursa olsun, düzenek denge durumundadır.
- m1 ≠ m2 olduğu zaman, kütleler ivmelenmeye başlayacaktır.
Sabit ivme denklemi

Kuvvet analizi kullanarak ivme üzerine bir denklem oluşturulabilir. Eğer kütlesiz ve genleştirilemeyen bir sicimi ve kütlesiz bir makarayı göz önünde bulundurursak, düşünmemiz gereken kuvvetler: gerilim kuvveti (T) ve iki objenin ağırlıkları (W1 ve W2) olacaktır. Ayrıca, ivmeyi hesaplayabilmek adına iki cisme de etki eden kuvvetleri dikkate almamız gerekir. Newton'ın hareket yasaları'dan ikincisini kullandığımız takdirde (m1 > m2 kabul ettiğimizde)ivme (a) için bir denklem sistemi elde ederiz.

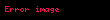

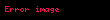
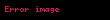
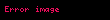

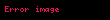
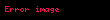
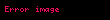
Ve iki denkleri topladığımız zaman elde ettiğimiz denklem:
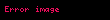
Ve ivme (a) için sonuçlanan formül:
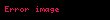
Diğer taraftan yer çekimine bağlı olarak oluşan ivme g de ağırlıkların hareketinin zamanlanmasıyla ve düzgün ivmenin hesaplanmasıyla bulunabilir: 
Atwood düzeneği bazen hareket denklenmelerini türeten 'nu göstermek amacıyla da kullanılır.
Gerilim denklemi
İpteki gerilimin denklemini bilmek kullanışlı olabilir. Gerilimi ölçmek için ivme denklemi, her iki kuvvet denkleminin yerine yazılır.
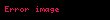
Örneğin 
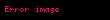
Eylemsizlik ve sürtünmeli makara denklemleri
m1 ve m2 arasındaki çok küçük kütle farklılıkları için, r yarıçaplı makaranın eylemsizlik momenti (I), ihmal edilemez. Makaranın açısal ivmesi:
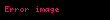

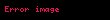
Newton'ın ikinci hareket kanunuyla birlikte, T1, T2 ve a çözülürse eğer şu sonuçları elde ederiz:
İvme:
m1 kütlesine etki eden ip gerilimi:
m2 kütlesine etki eden ip gerilimi:
Yatak sürtünmesini ihmal etmek gerekirse (fakat eylemsizlik momentini ve ipin sürtünmesini değil), bu eşitlikler aşağıdaki gibi sadeleştirilebilir.
İvme:
m1 kütlesine etki eden ip gerilmesi:
m2 kütlesine etki eden ip gerilmesi:
Ayrıca bakınız
Kaynakça
https://en.wikipedia.org/wiki/Atwood_machine 3 Mart 2015 tarihinde Wayback Machine sitesinde arşivlendi.
Dış bağlantılar
- Professor Greenslade's account on the Atwood Machine19 Ocak 2015 tarihinde Wayback Machine sitesinde .
- "Atwood's Machine20 Ocak 2015 tarihinde Wayback Machine sitesinde ." by Enrique Zeleny, .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Atwood duzenegi ya da Atwood makinesi 1784 yilinda Ingiliz matematikci tarafindan laboratuvarda kanunlarinin deneyleri yapilirken icat edilmistir Atwood duzenegi klasik mekanik prensiplerini gostermek adina kullanilan yaygin bir duzenektir Atwood duzenegi Ideal bir Atwood duzenegi m1 ve m2 kutleleri olmak uzere birbirlerine uzatilamayan kutlesiz bir ip ve yine kutlesiz bir makarayla baglanmak uzere iki kisimdan olusur m1 m2 oldugu zaman kutleler ne olursa olsun duzenek denge durumundadir m1 m2 oldugu zaman kutleler ivmelenmeye baslayacaktir Sabit ivme denklemiAtwood duzeneginde kutlelerin uzerine etki eden kuvvetlerin diyagrami m1 gt m2 olmasi kosulunda m1 kutlesi asagi dogru ivmelenirken m2 kutlesi yukari dogru ivmeleniyor Kuvvet analizi kullanarak ivme uzerine bir denklem olusturulabilir Eger kutlesiz ve genlestirilemeyen bir sicimi ve kutlesiz bir makarayi goz onunde bulundurursak dusunmemiz gereken kuvvetler gerilim kuvveti T ve iki objenin agirliklari W1 ve W2 olacaktir Ayrica ivmeyi hesaplayabilmek adina iki cisme de etki eden kuvvetleri dikkate almamiz gerekir Newton in hareket yasalari dan ikincisini kullandigimiz takdirde m1 gt m2 kabul ettigimizde ivme a icin bir denklem sistemi elde ederiz m1 displaystyle m 1 asagi dogru ivmelenirken ve m2 displaystyle m 2 yukari dogru ivmelenirken a degeri pozitif olsun O halde m1 displaystyle m 1 ve m2 displaystyle m 2 cisimlerinin agirliklari W1 m1g displaystyle W 1 m 1 g ve W2 m2g displaystyle W 2 m 2 g olacaktir m1 displaystyle m 1 e etki eden kuvvetler m1g T m1a displaystyle m 1 g T m 1 a m2 displaystyle m 2 e etki eden kuvvetler T m2g m2a displaystyle T m 2 g m 2 a Ve iki denkleri topladigimiz zaman elde ettigimiz denklem m1g m2g m1a m2a displaystyle m 1 g m 2 g m 1 a m 2 a Ve ivme a icin sonuclanan formul a gm1 m2m1 m2 displaystyle a g m 1 m 2 over m 1 m 2 Diger taraftan yer cekimine bagli olarak olusan ivme g de agirliklarin hareketinin zamanlanmasiyla ve duzgun ivmenin hesaplanmasiyla bulunabilir d 12at2 displaystyle d 1 over 2 at 2 Atwood duzenegi bazen hareket denklenmelerini tureten nu gostermek amaciyla da kullanilir Gerilim denklemiIpteki gerilimin denklemini bilmek kullanisli olabilir Gerilimi olcmek icin ivme denklemi her iki kuvvet denkleminin yerine yazilir a gm1 m2m1 m2 displaystyle a g m 1 m 2 over m 1 m 2 Ornegin m1a m1g T displaystyle m 1 a m 1 g T de yerine koydugumuzda su denklemi elde ederiz T 2gm1m2m1 m2 displaystyle T 2gm 1 m 2 over m 1 m 2 Eylemsizlik ve surtunmeli makara denklemlerim1 ve m2 arasindaki cok kucuk kutle farkliliklari icin r yaricapli makaranin eylemsizlik momenti I ihmal edilemez Makaranin acisal ivmesi a ar displaystyle alpha a over r a displaystyle alpha makaranin acisal ivmesidir Net tork ise tnet T1 T2 r tfriction Ia displaystyle tau mathrm net left T 1 T 2 right r tau mathrm friction I alpha Newton in ikinci hareket kanunuyla birlikte T1 T2 ve a cozulurse eger su sonuclari elde ederiz Ivme a g m1 m2 tfrictionrm1 m2 Ir2 displaystyle a g m 1 m 2 tau mathrm friction over r over m 1 m 2 I over r 2 m1 kutlesine etki eden ip gerilimi T1 m1g 2m2 Ir2 tfrictionrg m1 m2 Ir2 displaystyle T 1 m 1 g 2m 2 I over r 2 tau mathrm friction over rg over m 1 m 2 I over r 2 m2 kutlesine etki eden ip gerilimi T2 m2g 2m1 Ir2 tfrictionrg m1 m2 Ir2 displaystyle T 2 m 2 g 2m 1 I over r 2 tau mathrm friction over rg over m 1 m 2 I over r 2 Yatak surtunmesini ihmal etmek gerekirse fakat eylemsizlik momentini ve ipin surtunmesini degil bu esitlikler asagidaki gibi sadelestirilebilir Ivme a g m1 m2 m1 m2 Ir2 displaystyle a g m 1 m 2 over m 1 m 2 I over r 2 m1 kutlesine etki eden ip gerilmesi T1 m1g 2m2 Ir2 m1 m2 Ir2 displaystyle T 1 m 1 g 2m 2 I over r 2 over m 1 m 2 I over r 2 m2 kutlesine etki eden ip gerilmesi T2 m2g 2m1 Ir2 m1 m2 Ir2 displaystyle T 2 m 2 g 2m 1 I over r 2 over m 1 m 2 I over r 2 Ayrica bakinizMakara mekanik SurtunmeKaynakca Tipler Paul A 1991 Physics For Scientists and Engineers Third Edition Extended Version New York Worth Publishers ISBN 0 87901 432 6 Chapter 6 example 6 13 page 160 https en wikipedia org wiki Atwood machine 3 Mart 2015 tarihinde Wayback Machine sitesinde arsivlendi Dis baglantilarProfessor Greenslade s account on the Atwood Machine19 Ocak 2015 tarihinde Wayback Machine sitesinde Atwood s Machine20 Ocak 2015 tarihinde Wayback Machine sitesinde by Enrique Zeleny
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans