Bileşke kuvvet, katı cisimlerde cisme uygulanan tek bir kuvvet ve beraberindeki tork. Cisme, diğer bütün uygulanan kuvvetlerin toplamıyla aynı etkiyi yapar. Bu kuvvetin etkilediği yerin belirlenmesi tork bulmak açısından önemlidir. Bileşke kuvvet terimi sadece kuvveti değil beraberindeki torku da kapsamaktadır. Bazı kaynaklarda da bu yüzden bileşke kuvvet-tork diye geçer.
Örneklendirme
Buradaki örnekler basit yöntemlerle bileşke kuvveti bulmakla ilgili ufak bilgiler içerir.

1.Şekilde bileşke kuvvet bulmak için bu iki kuvvettin birleşme noktaları hesaba katılır. Örnekte olduğu gibi birleşebilen bu kuvvetin bileşkesi paralelkenar yöntemiyle rahatlıkla bulunabilir. Bu yöntemdeki amaç ortak kesişim noktasını gözlem noktası almaktır. Bu sayede tork her zaman sıfırdır ve bu sayede bileşke kuvvet net kuvvete eşittir.
2.Şekilde ise birbirine paralel iki kuvvetin bileşkesi alınmakta. Bu iki kuvvet paralel oldukları için direkt olarak birbirlerinin üzerine eklenerek işlem yapılabilir. Buradaki tork sorunu ise kuvvetlerin paralel ve aynı yönlü olması sayesinde kendiliğinden çözülür. Gözlem noktası farkı olmadan tork sıfıra eşittir.
Bağlı Vektör
Bir kuvvetin cisme uygulandığı bir etkime noktası vardır. Bu noktanın yerinin değişmesi kuvvetin cisim üzerinde yarattığı etkiyi değiştirir. Bu nedenle kuvvet etkime noktasına bağlı bir vektördür, yani kısaca bağlı bir vektördür.
Aynı noktaya etkiyen iki kuvvet veya aynı şekilde aynı noktadan başlayan iki vektör arasında işlem yapılabilir ve de bu yeni vektörün etkisi diğer iki vektörün toplam etkisiyle aynıdır. Fakat aynı etkime noktasına sahip olmayan vektörler arasında işlem yapılamaz.
Bir kuvvetin uygulanma noktasını değiştirmek o kadar da zor değildir. Kuvveti bilenşenlerine ayırıp, bunu yaparken de birbirine zıt yönlü eşit büyüklükte kuvvetler seçersek, götürmek istediğimiz yerde saf tork oluşacaktır ve de aynı zamanda etkime noktamız taşınmış. Bu yöntem kullanılarak kuvvetlerle işlemler kolaylıkla yapılabilir.
Bir cisme etkiyen bu kuvvetler bütününün tek bir noktaya taşınıp beraberinde torklarının da hesaplanmasıyla bileşke kuvvet-tork oluşur.
Tork
Eğer bir R noktası bileşke kuvvet F için etkime noktası olarak seçilirse, n kadar kuvvet için ve her bir kuvvet Fi için onunla alakalı olan tork T belirlendiğinde formüller:

ve

olarak ortaya çıkar.
Kullanışlı bir bilgi olarak şu da akılda kalmalıdır ki, etkileşim noktası R, bileşke kuvvetin uygulandığı doğrultu boyunca herhangi bir nokta olarak seçilebilir. Buna bağlı olarak tork da değişmeyecektir. Bunu ispatlamak için kF i kullanarak tork formülünü yazarsak

sonra da formülün sağ tarafını orijinal formül olarak ayırırsak
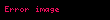
olur ve ikinci terim sıfır olduğu için F e bakacak olursak

çıkacaktır, bu nedenle de tork değişmeden kalır.
Torksuz Bileşke
Torkun sıfır olduğu bir etkime noktası düşünmek her zaman daha kolay ve yararlıdır.
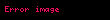
Yukarıda F bileşke kuvvet ve sistemdeki kuvvetler de Fi olarak belirtilmiştir.
Bu formülde de görüldüğü üzere R için bir çözüm olması için kuvvet ve etkileşim noktasının birbirine dik olması gerekiyor. İşte bu torksuz bileşke kuvvetin koşulu olarak karşımıza çıkıyor. Bunun matematiksel olarak

şeklinde yazabiliriz.
Eğer bu koşul sağlanırsa oluşacak sisteme saf kuvvet, fakat sağlanmadığı diğer bütün durumlarda ise saf tork denir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bileske kuvvet kati cisimlerde cisme uygulanan tek bir kuvvet ve beraberindeki tork Cisme diger butun uygulanan kuvvetlerin toplamiyla ayni etkiyi yapar Bu kuvvetin etkiledigi yerin belirlenmesi tork bulmak acisindan onemlidir Bileske kuvvet terimi sadece kuvveti degil beraberindeki torku da kapsamaktadir Bazi kaynaklarda da bu yuzden bileske kuvvet tork diye gecer OrneklendirmeBuradaki ornekler basit yontemlerle bileske kuvveti bulmakla ilgili ufak bilgiler icerir Rezultanta 1 Sekilde bileske kuvvet bulmak icin bu iki kuvvettin birlesme noktalari hesaba katilir Ornekte oldugu gibi birlesebilen bu kuvvetin bileskesi paralelkenar yontemiyle rahatlikla bulunabilir Bu yontemdeki amac ortak kesisim noktasini gozlem noktasi almaktir Bu sayede tork her zaman sifirdir ve bu sayede bileske kuvvet net kuvvete esittir 2 Sekilde ise birbirine paralel iki kuvvetin bileskesi alinmakta Bu iki kuvvet paralel olduklari icin direkt olarak birbirlerinin uzerine eklenerek islem yapilabilir Buradaki tork sorunu ise kuvvetlerin paralel ve ayni yonlu olmasi sayesinde kendiliginden cozulur Gozlem noktasi farki olmadan tork sifira esittir Bagli VektorBir kuvvetin cisme uygulandigi bir etkime noktasi vardir Bu noktanin yerinin degismesi kuvvetin cisim uzerinde yarattigi etkiyi degistirir Bu nedenle kuvvet etkime noktasina bagli bir vektordur yani kisaca bagli bir vektordur Ayni noktaya etkiyen iki kuvvet veya ayni sekilde ayni noktadan baslayan iki vektor arasinda islem yapilabilir ve de bu yeni vektorun etkisi diger iki vektorun toplam etkisiyle aynidir Fakat ayni etkime noktasina sahip olmayan vektorler arasinda islem yapilamaz Bir kuvvetin uygulanma noktasini degistirmek o kadar da zor degildir Kuvveti bilensenlerine ayirip bunu yaparken de birbirine zit yonlu esit buyuklukte kuvvetler secersek goturmek istedigimiz yerde saf tork olusacaktir ve de ayni zamanda etkime noktamiz tasinmis Bu yontem kullanilarak kuvvetlerle islemler kolaylikla yapilabilir Bir cisme etkiyen bu kuvvetler butununun tek bir noktaya tasinip beraberinde torklarinin da hesaplanmasiyla bileske kuvvet tork olusur TorkEger bir R noktasi bileske kuvvet F icin etkime noktasi olarak secilirse n kadar kuvvet icin ve her bir kuvvet Fi icin onunla alakali olan tork T belirlendiginde formuller F i 1nFi displaystyle mathbf F sum i 1 n mathbf F i ve T i 1n Ri R Fi displaystyle mathbf T sum i 1 n mathbf R i mathbf R times mathbf F i olarak ortaya cikar Kullanisli bir bilgi olarak su da akilda kalmalidir ki etkilesim noktasi R bileske kuvvetin uygulandigi dogrultu boyunca herhangi bir nokta olarak secilebilir Buna bagli olarak tork da degismeyecektir Bunu ispatlamak icin kF i kullanarak tork formulunu yazarsak T i 1n Ri R kF Fi displaystyle mathbf T sum i 1 n mathbf R i mathbf R k mathbf F times mathbf F i sonra da formulun sag tarafini orijinal formul olarak ayirirsak T i 1n Ri R Fi i 1nkF Fi i 1n Ri R Fi displaystyle mathbf T sum i 1 n mathbf R i mathbf R times mathbf F i sum i 1 n k mathbf F times mathbf F i sum i 1 n mathbf R i mathbf R times mathbf F i olur ve ikinci terim sifir oldugu icin F e bakacak olursak i 1nkF Fi kF i 1nFi 0 displaystyle sum i 1 n k mathbf F times mathbf F i k mathbf F times sum i 1 n mathbf F i 0 cikacaktir bu nedenle de tork degismeden kalir Torksuz BileskeTorkun sifir oldugu bir etkime noktasi dusunmek her zaman daha kolay ve yararlidir R F i 1nRi Fi displaystyle mathbf R times mathbf F sum i 1 n mathbf R i times mathbf F i Yukarida F bileske kuvvet ve sistemdeki kuvvetler de Fi olarak belirtilmistir Bu formulde de goruldugu uzere R icin bir cozum olmasi icin kuvvet ve etkilesim noktasinin birbirine dik olmasi gerekiyor Iste bu torksuz bileske kuvvetin kosulu olarak karsimiza cikiyor Bunun matematiksel olarak F i 1nRi Fi 0 displaystyle mathbf F cdot sum i 1 n mathbf R i times mathbf F i 0 seklinde yazabiliriz Eger bu kosul saglanirsa olusacak sisteme saf kuvvet fakat saglanmadigi diger butun durumlarda ise saf tork denir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans