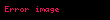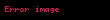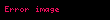Tümleşik matematikte binom dönüşümü bir dizinin hesaplamaya yarayan bir . Kavram, binom dönüşümünün Euler dizisine uygulanması sonucu oluşan Euler dönüşümüyle yakından ilintilidir.
Tanım
Bir 
olarak tanımlanan 

Bu dönüşüm bir .
Bu, farklı bir biçimde de gösterilebilir.
Burada δ göstermektedir.
işlemiyle özgün diziye geri dönülebilir.
Bir dizinin binom dönüşümü o dizinin n. .
Burada Δ simgelemektedir.
Binom dönüşümü zaman zaman ek bir imle gösterilmektedir. Bu gösterimde dönüşüm
biçiminde ifade edilirken bu ifadenin tersi
olarak yazılır.
Örnek
Binom dönüşümleri fark tablolarında kolaylıkla gözlenebilmektedir.
| 0 | 1 | 10 | 63 | 324 | 1485 | |||||
| 1 | 9 | 53 | 261 | 1161 | ||||||
| 8 | 44 | 208 | 900 | |||||||
| 36 | 164 | 692 | ||||||||
| 128 | 528 | |||||||||
| 400 |
0, 1, 10, 63, 324, 1485, … biçimindeki en üst satır (

Değişim durumları
Binom dönüşümü Bell sayılarının . Başka bir deyişle,
eşitliği sağlanmaktadır. Burada 
Olağan üretici işlev
Dönüşüm, diziyle ilişkilendirilmiş birbirine bağlamaktadır. için
ve
eşitliklerinin sağlandığı varsayılsın. Buradan
ifadesine ulaşılabilir.
Euler dönüşümü
Olağan üretici işlevler arasındaki ilişki zaman zaman Euler dönüşümü olarak adlandırılmaktadır. İki farklı biçimde var olan dönüşüm, almaşık dizilerin yakınsaklığını hızlandırabilmektedir. Başka bir deyişle,
ifadesinde x yerine 1/2 konularak 1'e ulaşılabilir. Sağdaki terimler çok hızlı bir biçimde küçüldüklerinden bu toplam kolaylıkla hesaplanabilir.
Euler dönüşümü şu biçimde genellenbilir:
p = 0, 1, 2, … için
eşitliği sağlanır.
Euler dönüşümü 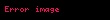
olarak ifade edilebilmektedir.
Binom dönüşümü ve bunun farklı bir uyarlaması olan Euler dönüşümü bir sayının olarak ifade edilmesinde büyük önem taşımaktadır. 
olduğu varsayılsın. Buradan
ve
sonuçlarına ulaşılabilmektedir.
Üstel üretici işlev
için
ve
eşitliklerinin sağlandığı varsayılsın. Buradan
eşitliğine ulaşılır.
, olağan üretici işlevi üstel üretici işleve dönüştürebilmektedir.
İntegral biçimindeki ifadesi
Dizi bir karmaşık çözümleme işleviyle değiştirildiğinde dizinin binom dönüşümü biçiminde ifade edilebilmektedir.
Genellemeler
Prodinger bir dönüşümden söz etmektedir.
eşitliğinin sağlandığı varsayıldığında
ifadesine ulaşılır. Burada U ve B sırasıyla 

Artan k-binom dönüşümü zaman zaman
biçiminde, azalan k-binom dönüşümü
biçiminde tanımlanmaktadır. Her iki dönüşüm de eşittir.
Binom dönüşümü
olarak tanımlanır, bu ifade

işlevine eşitlenir, yeni bir tablosu oluşturulur ve bu tablonun her satırının ilk elemanından 
ifadesine eşit olur.
Aynı işlem k kez yinelendiğinde
eşitliğine ulaşılır. Bu ifadenin tersi
olarak yazılır.
Bu ifadenin genel biçimi
olarak yazılabilir. Burada 
Bu ifadenin tersi
biçiminde gösterilir.
Ayrıca bakınız
Kaynakça
- John H. Conway & Richard K. Guy, 1996, The Book of Numbers
- Donald E. Knuth, The Art of Computer Programming Cilt 3, (1973) Addison-Wesley, Reading, MA.
- Helmut Prodinger, 1992, Some information about the Binomial transform12 Mart 2007 tarihinde Wayback Machine sitesinde .
- Michael Z. Spivey & Laura L. Steil, 2006, The k-Binomial Transforms and the Hankel Transform2 Nisan 2015 tarihinde Wayback Machine sitesinde .
- Borisov B. & Shkodrov V., 2007, Divergent Series in the Generalized Binomial Transform, Adv. Stud. Cont. Math., 14 (1): 77-82
Dış bağlantılar
- Binom Dönüşümü2 Nisan 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Tumlesik matematikte binom donusumu bir dizinin hesaplamaya yarayan bir Kavram binom donusumunun Euler dizisine uygulanmasi sonucu olusan Euler donusumuyle yakindan ilintilidir TanimBir an displaystyle a n dizisinin binom donusumu T sn k 0n 1 k nk ak displaystyle s n sum k 0 n 1 k n choose k a k olarak tanimlanan sn displaystyle s n dizisidir Ta n sn displaystyle Ta n s n yaziminda T bir sonsuz boyutlu gostermektedir Bu islecin elemanlari su bicimde gosterilebilir sn Ta n k 0 Tnkak displaystyle s n Ta n sum k 0 infty T nk a k Bu donusum bir TT 1 displaystyle TT 1 Bu farkli bir bicimde de gosterilebilir k 0 TnkTkm dnm displaystyle sum k 0 infty T nk T km delta nm Burada d gostermektedir an k 0n 1 k nk sk displaystyle a n sum k 0 n 1 k n choose k s k islemiyle ozgun diziye geri donulebilir Bir dizinin binom donusumu o dizinin n s0 a0 displaystyle s 0 a 0 s1 a 0 a1 a0 displaystyle s 1 triangle a 0 a 1 a 0 s2 2a 0 a2 a1 a1 a0 a2 2a1 a0 displaystyle s 2 triangle 2 a 0 a 2 a 1 a 1 a 0 a 2 2a 1 a 0 displaystyle dots sn 1 n na 0 displaystyle s n 1 n triangle n a 0 Burada D simgelemektedir Binom donusumu zaman zaman ek bir imle gosterilmektedir Bu gosterimde donusum tn k 0n 1 n k nk ak displaystyle t n sum k 0 n 1 n k n choose k a k biciminde ifade edilirken bu ifadenin tersi an k 0n nk tk displaystyle a n sum k 0 n n choose k t k olarak yazilir OrnekBinom donusumleri fark tablolarinda kolaylikla gozlenebilmektedir 0 1 10 63 324 1485 1 9 53 261 1161 8 44 208 900 36 164 692 128 528 400 0 1 10 63 324 1485 bicimindeki en ust satir 2n2 n 3n 2 displaystyle 2n 2 n 3 n 2 tarafindan tanimlanan bir dizi 0 1 8 36 128 400 kosegeninin n22n 1 displaystyle n 2 2 n 1 tarafindan tanimlanan bir dizi binom donusumudur Degisim durumlariBinom donusumu Bell sayilarinin Baska bir deyisle Bn 1 k 0n nk Bk displaystyle B n 1 sum k 0 n n choose k B k esitligi saglanmaktadir Burada Bn displaystyle B n Bell sayilarini gostermektedir Olagan uretici islevDonusum diziyle iliskilendirilmis birbirine baglamaktadir icin f x n 0 anxn displaystyle f x sum n 0 infty a n x n ve g x n 0 snxn displaystyle g x sum n 0 infty s n x n esitliklerinin saglandigi varsayilsin Buradan g x Tf x 11 xf xx 1 displaystyle g x Tf x frac 1 1 x f left frac x x 1 right ifadesine ulasilabilir Euler donusumuOlagan uretici islevler arasindaki iliski zaman zaman Euler donusumu olarak adlandirilmaktadir Iki farkli bicimde var olan donusum almasik dizilerin yakinsakligini hizlandirabilmektedir Baska bir deyisle n 0 1 nan n 0 1 nDna02n 1 displaystyle sum n 0 infty 1 n a n sum n 0 infty 1 n frac Delta n a 0 2 n 1 ifadesinde x yerine 1 2 konularak 1 e ulasilabilir Sagdaki terimler cok hizli bir bicimde kuculduklerinden bu toplam kolaylikla hesaplanabilir Euler donusumu su bicimde genellenbilir p 0 1 2 icin n 0 1 n n pn an n 0 1 n n pn Dna02n p 1 displaystyle sum n 0 infty 1 n n p choose n a n sum n 0 infty 1 n n p choose n frac Delta n a 0 2 n p 1 esitligi saglanir Euler donusumu 2F1 displaystyle 2 F 1 siklikla uygulanmkatadir Bu durumda Euler donusumu 2F1 a b c z 1 z b2F1 c a b c zz 1 displaystyle 2 F 1 a b c z 1 z b 2 F 1 left c a b c frac z z 1 right olarak ifade edilebilmektedir Binom donusumu ve bunun farkli bir uyarlamasi olan Euler donusumu bir sayinin olarak ifade edilmesinde buyuk onem tasimaktadir 0 lt x lt 1 displaystyle 0 lt x lt 1 sayisinin surekli kesir ifadesinin x 0 a1 a2 a3 displaystyle x 0 a 1 a 2 a 3 cdots oldugu varsayilsin Buradan x1 x 0 a1 1 a2 a3 displaystyle frac x 1 x 0 a 1 1 a 2 a 3 cdots ve x1 x 0 a1 1 a2 a3 displaystyle frac x 1 x 0 a 1 1 a 2 a 3 cdots sonuclarina ulasilabilmektedir Ustel uretici islevicin f x n 0 anxnn displaystyle overline f x sum n 0 infty a n frac x n n ve g x n 0 snxnn displaystyle overline g x sum n 0 infty s n frac x n n esitliklerinin saglandigi varsayilsin Buradan g x Tf x exf x displaystyle overline g x T overline f x e x overline f x esitligine ulasilir olagan uretici islevi ustel uretici isleve donusturebilmektedir Integral bicimindeki ifadesiDizi bir karmasik cozumleme isleviyle degistirildiginde dizinin binom donusumu biciminde ifade edilebilmektedir GenellemelerProdinger bir donusumden soz etmektedir un k 0n nk ak c n kbk displaystyle u n sum k 0 n n choose k a k c n k b k esitliginin saglandigi varsayildiginda U x 1cx 1B axcx 1 displaystyle U x frac 1 cx 1 B left frac ax cx 1 right ifadesine ulasilir Burada U ve B sirasiyla un displaystyle u n ve bn displaystyle b n dizileriyle iliskilendirilmis olagan uretici islevleri gostermektedir Artan k binom donusumu zaman zaman j 0n nj jkaj displaystyle sum j 0 n n choose j j k a j biciminde azalan k binom donusumu j 0n nj jn kaj displaystyle sum j 0 n n choose j j n k a j biciminde tanimlanmaktadir Her iki donusum de esittir Binom donusumu i 0n 1 n i ni ai bn displaystyle sum i 0 n 1 n i binom n i a i b n olarak tanimlanir bu ifade J a n bn displaystyle mathfrak J a n b n islevine esitlenir yeni bir tablosu olusturulur ve bu tablonun her satirinin ilk elemanindan bn displaystyle b n gibi yeni bir dizi olusturulursa ozgun dizinin ikinci binom donusumu J2 a n i 0n 2 n i ni ai displaystyle mathfrak J 2 a n sum i 0 n 2 n i binom n i a i ifadesine esit olur Ayni islem k kez yinelendiginde Jk a n bn i 0n k n i ni ai displaystyle mathfrak J k a n b n sum i 0 n k n i binom n i a i esitligine ulasilir Bu ifadenin tersi J k b n an i 0nkn i ni bi displaystyle mathfrak J k b n a n sum i 0 n k n i binom n i b i olarak yazilir Bu ifadenin genel bicimi Jk a n bn E k na0 displaystyle mathfrak J k a n b n mathbf E k n a 0 olarak yazilabilir Burada E displaystyle mathbf E gostermektedir Bu ifadenin tersi J k b n an E k nb0 displaystyle mathfrak J k b n a n mathbf E k n b 0 biciminde gosterilir Ayrica bakinizEuler toplamiKaynakcaJohn H Conway amp Richard K Guy 1996 The Book of Numbers Donald E Knuth The Art of Computer Programming Cilt 3 1973 Addison Wesley Reading MA Helmut Prodinger 1992 Some information about the Binomial transform12 Mart 2007 tarihinde Wayback Machine sitesinde Michael Z Spivey amp Laura L Steil 2006 The k Binomial Transforms and the Hankel Transform2 Nisan 2015 tarihinde Wayback Machine sitesinde Borisov B amp Shkodrov V 2007 Divergent Series in the Generalized Binomial Transform Adv Stud Cont Math 14 1 77 82Dis baglantilarBinom Donusumu2 Nisan 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State