Cantor'un köşegen yöntemi

Georg Cantor'un doğal sayılar ile reel sayıların birebir eşlemesinin yapılamayacağını göstermek için geliştirdiği yöntem. Böyle bir eşlemenin yokluğu sonsuz elemanlı kümelerin büyüklüklerinin karşılaştırılması kavramının gelişimi açısından son derece önemlidir.

Georg Cantor

Büyüklük

Verilen bir A kümesinin en az B kümesi kadar büyük olması B'den A'ya bir birebir fonksiyonun var olması şeklinde tanımlanır (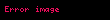${\displaystyle A\geq B}$ yazılır). Böylelikle B'nin bir kopyasının A'nın içerisinde bulunabiliyor olması sağlanır. Eğer aynı şekilde B'den de A'ya bir birebir fonksiyon varsa o zaman bu iki küme eşit büyüklükte denir (${\displaystyle B\simeq A}$ yazılır).

• Örnek olarak Çift Tam Sayılar Kümesi'nin (${\displaystyle 2\mathbb {Z} =\{...,-4,-2,0,2,4,...\}}$) ile Tam Sayılar Kümesi ${\displaystyle (\mathbb {Z} =\{...,-3,-2,-1,0,1,2,...\})}$ düşünülebilir. ${\displaystyle 2\mathbb {Z} }$'nin elemanları ${\displaystyle \mathbb {Z} }$'nin içerisinde kendi kendilerine gönderilir.

İspat

0 ile 1 arasındaki reel sayılar kümesinin sayılabilir olduğunu varsayalım. Buna göre 0 ile 1 arasındaki her reel sayıya karşılık doğal sayılar kümesinde bir sayı gelmelidir. Yani iki küme birebir eşlenebilir diyoruz. Böyle bir eşlemeyi ele alalım ve 0 ile 1 arasındaki reel sayıları verilen eşleşmeye göre sıralayarak bir liste elde edelim. Bu listede sayıları küçükten büyüğe gelecek şekilde sıralamadım(bu şekilde sıralamaya gerek yoktur bu kısma takılmayın). Aşağıdaki sadece ilk 4 eşleşmeyi yazdım. Bu eşleşmenin sonsuza kadar gittiğini varsayıyoruz(önemli olan nokta burasıdır). Dolayısıyla aslında aşağıdaki birebir eşleşmede tüm doğal sayılar ve 0-1 aralığındaki tüm reel sayılar var diyoruz.

 0 ile 1 arasındaki tüm reel sayıları yazdığımızı diğer bir deyişle yazabileceğimizi iddia etmiştik. Şimdi bunun aksini kanıtlayalım. 

 0 ile 1 arasında olan öyle bir sayı bulalım ki: Bu sayıya C adını verelim ve onu şu kurala göre oluşturalım: 

Birinci sayının ilk ondalık basamağına bakalım ve buradaki rakamdan farklı herhangi bir rakamı seçip C sayısının ilk basamağı olarak yazalım, aynı şekilde C'nin ikinci, üçüncü,... basamaklarını da oluşturalım. Mesela eğer 0 la 1 arasındaki reel sayılar aşağıdaki gibi sıralanmışsa:

s0 = 0,13567....... ^ s1 = 0,25678....... ^ s2 = 0,00212....... ^ s3 = 0,14291....... ^ . . . 

C sayısının ilk basamağını 1'den farklı, 2. basamağını 5'ten farklı, 3. basamağını 2'den farklı, 4. basamağını gene 9'dan farklı birer rakam olarak seçeriz. (Varsayımımıza göre) Bu şekilde devam ederek 0 ile 1 arasındaki tüm sayıları tararız. Hatırlayın : taradığımız her reel sayıya karşılık doğal sayılar kümesinde bir sayı var(birebir eşleşme).

0 ile 1 arasında var olan tüm sayıları taradık(bu sayılara baktık) ve yukarıdaki anlattığımız yol ile bir C sayısı bulduk. C sayısının 0 ile 1 arasında olduğunu ve 0 ile 1 arasındaki tüm sayıları taradığımızı varsaymıştık. O halde taradığımız sayılardan birisi C sayısı olmalı. Halbuki C sayısı bizim taradığımız sayılardan hiçbirine eşit değil çünkü C sayısını buna göre oluşturmuştuk zaten. Gördüğünüz gibi burada bir tezatlık var. 0 ile 1 arasındaki tüm sayıları tek tek taradığımızı kabul ediyoruz.Ama elimizde 0 ile 1 aralığında öyle bir C sayısı bulduk ki taradığımız tüm sayılardan farklı. Dolayısıyla bu C sayısına karşılık gelebilecek bir doğal sayı da yok. Demek ki varsaydığımız birebir eşleme mümkün değil ve aslında reel sayılar kümesindeki eleman sayısı doğal sayılar kümesindeki eleman sayısından daha fazla. O zaman 0 ile 1 arasındaki reel sayılar kümesi sayılamaz deriz.