Bu madde, uygun değildir. (Ocak 2012) |
Compton olayı (veya Compton saçılması), yüksek enerjili X ışınlarının fotonu ile karbon atomunun serbest elektronunun çarpıştırılması sonucu elektronun ve fotonun şekildeki gibi saçılması olayıdır.
20. yüzyılın başlarında, X-ışınlarının madde ile etkileşimi araştırılmaya devam edildi. Θ ve θ ile ilgili farklı bir dalga boyunda ortaya bilinen bir dalga boyu X-ışınları atomları ile etkileşime girdiğinde, X-ışınları bir açı içine dağılmış olduğu gözlendi. Klasik elektromanyetizma dağınık ışınların dalga boyu, ilk dalga boyuna eşit olması gerektiğini tahmin edilse de, ilk dalga boyu daha büyük olduğunu bulmuştur. Compton 1923 yılında, Einstein'ın ışık unsurları, sadece ışık frekansına bağlı olarak belirli bir miktarda enerji içeren "nicemlenmiş" olarak kavramsallaştırdığı kanısına vardı "fotonlar" parçacık gibi ivmeli hareket ederek X-ray yıldız kayması açıkladı. Physical Review bir bildiri yayınladı. Compton dalgaboyu ve her dağınık X-ışını (foton) sadece tek bir elektron ile etkileşim olduğunu varsayarak X-ışınları saçılma açısı arasında matematiksel bir ilişki türetilmiştir. Onun türevi ilişkisi doğrulandı. Deneyler rapor ederek sonuca varıyor ve:

Not: Bu sayfadaki bütün formüllerde:
- Joule birimi yerine Elektronvolt,
- metre birimi yerine Ångström,
- metre/saniye birimi yerine Ångström/saniye (Ångström bölü saniye) kullanılabilir.
Burada;
: saçılma öncesinde fotonun dalga boyu, metre biriminde,
: saçılma sonrasında fotonun dalga boyu, metre biriminde,
: Planck sabiti, aşağıdaki h/mc sabitine bakınız,
: Elektronun durgun haldeki kütlesi, aşağıdaki h/mc sabitine bakınız,
: ışık hızı, aşağıdaki h/mc sabitine bakınız,
: fotonun saçılma açısıdır.
sabit bir sayıdır ve Compton dalgaboyu olarak bilinir. Değeri: Ångströmdür. (Ångström, "Å" sembolü ile gösterilir). Compton dalgaboyu, Ångström cinsinden yazıldığı için fotonun dalgaboyu da Ångström cinsinden belirlenecektir.
Compton dalgaboyunun metre biriminden değeri: metredir. Compton dalgaboyu, metre cinsinden yazıldığı için fotonun dalgaboyu da metre cinsinden belirlenecektir.
Λ dalga boyu kayması '- λ en az sıfır (örneğin θ = 0 °)ve en fazla iki kez elektronun Comptondalga boyu (θ = 180 °). Compton, bazı X-ışınları geniş açılar dağılmış olmasına rağmen herhangi bir dalga boyukayması yaşadığını, bu gibi durumlarda her foton bir elektron çıkarmak için başarısız oldu. Böylece vardiya büyüklüğü elektronun Compton dalga boyu değil, ama yukarı 10 000 kat daha küçük olabilir, tüm atom Compton dalgaboyu ile ilgilidir.
Compton olayının özellikleri
Compton olayında enerji korunumu
Compton olayında enerji korunur. Formülü:
olduğu için:
Burada;
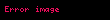
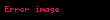

Compton olayında hız, dalga boyu ve frekans
Gelen foton ve saçılan fotonun hızı; "c" ışık hızı kadardır.
formülünü endeks olarak alırsak dalga boyu ile frekans ters orantılıdır.
O halde:
sonucuna ulaşılır.
Burada;
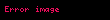


Not: Bu sayfadaki bütün formüllerde:
Kaynakça
- İngilizce Vikipedi maddesi 10 Kasım 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- [1] 9 Şubat 2013 tarihinde Wayback Machine sitesinde arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Ocak 2012 Compton olayi veya Compton sacilmasi yuksek enerjili X isinlarinin fotonu ile karbon atomunun serbest elektronunun carpistirilmasi sonucu elektronun ve fotonun sekildeki gibi sacilmasi olayidir 20 yuzyilin baslarinda X isinlarinin madde ile etkilesimi arastirilmaya devam edildi 8 ve 8 ile ilgili farkli bir dalga boyunda ortaya bilinen bir dalga boyu X isinlari atomlari ile etkilesime girdiginde X isinlari bir aci icine dagilmis oldugu gozlendi Klasik elektromanyetizma daginik isinlarin dalga boyu ilk dalga boyuna esit olmasi gerektigini tahmin edilse de ilk dalga boyu daha buyuk oldugunu bulmustur Compton 1923 yilinda Einstein in isik unsurlari sadece isik frekansina bagli olarak belirli bir miktarda enerji iceren nicemlenmis olarak kavramsallastirdigi kanisina vardi fotonlar parcacik gibi ivmeli hareket ederek X ray yildiz kaymasi acikladi Physical Review bir bildiri yayinladi Compton dalgaboyu ve her daginik X isini foton sadece tek bir elektron ile etkilesim oldugunu varsayarak X isinlari sacilma acisi arasinda matematiksel bir iliski turetilmistir Onun turevi iliskisi dogrulandi Deneyler rapor ederek sonuca variyor ve Compton olayi Not Bu sayfadaki butun formullerde Joule birimi yerine Elektronvolt metre birimi yerine Angstrom metre saniye birimi yerine Angstrom saniye Angstrom bolu saniye kullanilabilir l SACILANFOTON l GELENFOTON hme c 1 cos 8 displaystyle lambda SACILANFOTON lambda GELENFOTON frac h m e cdot c 1 cos theta Burada l GELENFOTON displaystyle lambda GELENFOTON sacilma oncesinde fotonun dalga boyu metre biriminde l SACILANFOTON displaystyle lambda SACILANFOTON sacilma sonrasinda fotonun dalga boyu metre biriminde h displaystyle h Planck sabiti asagidaki h mc sabitine bakiniz me displaystyle m e Elektronun durgun haldeki kutlesi asagidaki h mc sabitine bakiniz c displaystyle c isik hizi asagidaki h mc sabitine bakiniz 8 displaystyle theta fotonun sacilma acisidir hme c displaystyle frac h m e cdot c sabit bir sayidir ve Compton dalgaboyu olarak bilinir Degeri 0 024 displaystyle 0 024 Angstromdur Angstrom A sembolu ile gosterilir Compton dalgaboyu Angstrom cinsinden yazildigi icin fotonun dalgaboyu da Angstrom cinsinden belirlenecektir Compton dalgaboyunun metre biriminden degeri 2 43x10 12 displaystyle 2 43x10 12 metredir Compton dalgaboyu metre cinsinden yazildigi icin fotonun dalgaboyu da metre cinsinden belirlenecektir L dalga boyu kaymasi l en az sifir ornegin 8 0 ve en fazla iki kez elektronun Comptondalga boyu 8 180 Compton bazi X isinlari genis acilar dagilmis olmasina ragmen herhangi bir dalga boyukaymasi yasadigini bu gibi durumlarda her foton bir elektron cikarmak icin basarisiz oldu Boylece vardiya buyuklugu elektronun Compton dalga boyu degil ama yukari 10 000 kat daha kucuk olabilir tum atom Compton dalgaboyu ile ilgilidir Compton olayinin ozellikleriCompton olayinda enerji korunumu Compton olayinda enerji korunur Formulu EGELENFOTON ESACILANFOTON EELEKTRON displaystyle E GELENFOTON E SACILANFOTON E ELEKTRON oldugu icin h v GELENFOTON h v SACILANFOTON EELEKTRON displaystyle h cdot v GELENFOTON h cdot v SACILANFOTON E ELEKTRON dd Burada E displaystyle E Enerji Joule J biriminde h displaystyle h Planck sabiti J s biriminde v displaystyle v hiz sembolu degildir fotonun frekansi s 1 birimindedir Compton olayinda hiz dalga boyu ve frekans Gelen foton ve sacilan fotonun hizi c isik hizi kadardir c v l displaystyle c v cdot lambda formulunu endeks olarak alirsak dalga boyu ile frekans ters orantilidir O halde v GELENFOTON gt v SACILANFOTON displaystyle v GELENFOTON gt v SACILANFOTON l SACILANFOTON gt l GELENFOTON displaystyle lambda SACILANFOTON gt lambda GELENFOTON sonucuna ulasilir Burada c displaystyle c isik hizi metre bolu saniye biriminde v displaystyle v hiz sembolu degildir fotonun frekansi s 1 biriminde l displaystyle lambda fotonun dalga boyu metre birimindedir Not Bu sayfadaki butun formullerde Joule birimi yerine Elektronvolt metre birimi yerine Angstrom metre saniye birimi yerine Angstrom saniye Angstrom bolu saniye kullanilabilir KaynakcaIngilizce Vikipedi maddesi 10 Kasim 2011 tarihinde Wayback Machine sitesinde arsivlendi 1 9 Subat 2013 tarihinde Wayback Machine sitesinde arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans