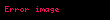D'Alembert işlemcisi, özel görelilikte, elektromanyetizmada ve ; Minkowski uzayını ve Einstein alan denklemlerinin diğer çözümlerini sağlayan Laplace işlemcisine d'Alembert işlemcisi veya dalga işlemcisi denir.
İşlemci, ya da olarak da gösterilebilir. Kare olmasının nedeni 4 boyutlu Minkowski uzayını temsil ediyor olmasıdır. Aynı şekilde Laplace işlemcisindeki simgesi de 3 boyutlu uzayı temsil etmektedir. Kuantum alan kuramında daha çok gösterimi yeğlenir.
Tanım
Minkowski uzayında d'Alembert işlemcisinin açık tanımı, c ışık hızı olmak üzere,
şeklindedir. Burada açıkça görüleceği gibi uzay 4 boyutludur. Ancak sâdelik adına (x,y,z,t) koordinatları yerine (x,y,z,ict) seçilerek,
biçimine dönüşür. Burada i sanal birim]dir.
Einstein toplam uzlaşımı ile 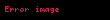

olarak ifâde edilebilir ki burada 
Ayrıca Laplace işlemcisi ile de tanımlanabilir:
Fizikte d'Alembert işlemcisi
Dalga denklemi, d'Alembert işlemcisi ile ifâde edilebilir:
burada 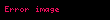
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
D Alembert islemcisi ozel gorelilikte elektromanyetizmada ve Minkowski uzayini ve Einstein alan denklemlerinin diger cozumlerini saglayan Laplace islemcisine d Alembert islemcisi veya dalga islemcisi denir Islemci displaystyle square ya da 2 displaystyle square 2 olarak da gosterilebilir Kare olmasinin nedeni 4 boyutlu Minkowski uzayini temsil ediyor olmasidir Ayni sekilde Laplace islemcisindeki 2 displaystyle nabla 2 simgesi de 3 boyutlu uzayi temsil etmektedir Kuantum alan kuraminda daha cok 2 displaystyle partial 2 gosterimi yeglenir TanimMinkowski uzayinda d Alembert islemcisinin acik tanimi c isik hizi olmak uzere 2 x2 2 y2 2 z2 1c2 2 t2 displaystyle square partial 2 over partial x 2 partial 2 over partial y 2 partial 2 over partial z 2 frac 1 c 2 partial 2 over partial t 2 seklindedir Burada acikca gorulecegi gibi uzay 4 boyutludur Ancak sadelik adina x y z t koordinatlari yerine x y z ict secilerek 2 x2 2 y2 2 z2 2 ict 2 displaystyle square partial 2 over partial x 2 partial 2 over partial y 2 partial 2 over partial z 2 partial 2 over partial ict 2 bicimine donusur Burada i sanal birim dir Einstein toplam uzlasimi ile m 0 1 2 3 ict x y z displaystyle mu 0 1 2 3 ict x y z koordinatlar ve m xm displaystyle partial mu partial over partial x mu turevler olmak uzere d Alembert islemcisi 2 m m hnm n m displaystyle square partial 2 partial mu partial mu eta nu mu partial nu partial mu olarak ifade edilebilir ki burada hnm displaystyle eta nu mu Ayrica Laplace islemcisi ile de tanimlanabilir 2 1c2 2 t2 displaystyle square nabla 2 1 over c 2 partial 2 over partial t 2 Fizikte d Alembert islemcisiDalga denklemi d Alembert islemcisi ile ifade edilebilir PS 0 displaystyle square Psi 0 burada PS displaystyle Psi dalga fonksiyonudur
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State