Fizikte, dairesel hareket bir nesnenin dairesel bir yörünge boyunca bir rotasyon ya da çemberin çevresinde yaptığı harekettir. Rotasyonun (ve sürekli hızın) sürekli açısal değeriyle birlikte düzgün ya da değişen rotasyon değeriyle düzensiz olabilir. 3 boyutlu bir cismin sabit ekseni etrafındaki rotasyon parçalarının dairesel hareketini içerir. Hareketin denkliği bir cisim kütlesinin merkezini tanımlar.
Dairesel hareketin örnekleri şunları içerir: sabit ağırlıkta Dünya yörüngesinde dönen yapay bir uydu, bir ipe bağlanmış ve daireler şeklinde sallanan bir taş, parkurda viraj boyunca dönen bir araba, düzgün bir manyetik alana dikey olarak hareket eden bir elektron ve bir mekanizmanın içerisinde dönen bir dişli. Nesnenin sürat vektörü sürekli yön değiştirdiği için, hareket eden nesne rotasyon merkezinin yöndeki merkezcil bir kuvvet tarafından ivme kazandırılıyor. Newton’un hareket yasalarına göre bu ivme olmadan nesne düz bir çizgide hareket eder.
Üniform



Fizikte, düzgün dairesel hareket dairesel bir yörüngeyi sabit süratle geçen bir cismin hareketini tanımlar. Cisminin rotasyon ekseninden uzaklığı her zaman sabit kalır. Cismin süratinin sabit olmasına rağmen, hızı sabit değildir: hız, vektörel bir büyüklük, hem cismin süratine hem gidiş yönüne bağlıdır. Bu değişken hız bir ivmenin varlığını gösterir; bu merkezcil ivme düzgün genlikten kaynaklanır ve her zaman rotasyon eksenine doğru yönlendirilir. Bu ivme dolayısıyla aynı şekilde genlikte düzgün ve rotasyon eksenine doğru yönlendirilmiş merkezcil bir güç tarafından üretilir.
Yörüngenin yarıçapına oranla göz ardı edilebilecek küçüklükte olmayan sert bir cismin sabit ekseni etrafındaki rotasyon durumunda, cismin her bir parçacığı aynı açısal sürat fakat konum ve yörüngeye bağlı olarak değişen sürat ve ivmeli bir düzgün dairesel hareket tanımlar.
Formüller

r yarıçaplı bir dairede hareket için, dairenin çevresi C = 2π r’dir. Bir tam dönüş için periyot T, aynı zamanda açısal sürat olarak bilinen rotasyonun açısal değeri, ise ω :
Ve birimler radyan/saniye’dir.
Daireyi dolaşan nesnenin hızı:
T sürede süpürülen θ açısı:
Yöndeki değişiklikten kaynaklanan ivme:
Vektörel ilişkiler Şekil 1’de gösteriliyor. Rotasyon ekseni ω = dθ / dt genliğiyle ve yörünge düzlemine dik Ω vektörü olarak gösterilmiştir. Ω vektörünün yönü sağ el kuralı kullanılarak bulunmuştur. Rotasyon belirlemek için olan bu kuralla, sürat vektör çarpı ürün olarak verilir; F burada vektör hem Ω hem de r (t)’ye dikey, yörüngeye teğet ve ω r genliğindedir.
Aynı şekilde, ivme :
En basit olarak hız, kütle ve yarıçap sabittir.
Bir kilogramlık bir cismin saniyede bir radyanın açısal süratiyle bir metre yarıçap etrafında dairesel olarak hareket ettiğini varsayalım.
•Hız saniyede 1 metredir. •İçeriye doğru ivme 1 m / s2’dir. •1 m / s2’de 1 kilogram merkezcil güce bağlıdır ve bu bir newton eder. •Cismin momentumu 1 kg•m•s−1’dir. •Eylemsizlik momentumu 1 kg•m²’dir. •Açısal momentumu 1 kg•m²•s−1’dir. •Kinetik enerji ½ jouledür. •Yörüngenin çevresi 2π (~ 6.283) metredir. •Hareketin devri dönüş başında 2π saniyedir. •Frekans (2π)−1 hertz’dir.
Kutupsal Koordinatlar

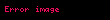 and
and 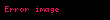 in the unit vectors
in the unit vectors 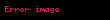 and
and 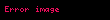 for a small increment
for a small increment  in angle
in angle 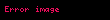 .
.Dairesel hareket boyunca cisim herhangi bir referans yönden konumlandırılmış θ (t) açısında orijin olarak alınan yörüngenin merkezinden R sabit uzaklığı olan kutupsal koordinat sistemi olarak tanımlanabilecek bir eğride hareket eder.
Bakınız Şekil 2. 

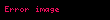


Hız yerdeğişimin zamana göre türevidir:
Dairenin yarıçapı sabit olduğundan, hızın radyal bileşeni sıfırdır. 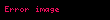

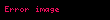
Bakınız Şekil 2’deki solda birim daire. Bu yüzden,
Değişimin yönü 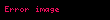

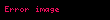
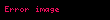
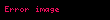
İşaret pozitif çünkü dθ’daki artış nesne ve 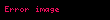

Bu yüzden hız,
haline geliyor.
Cismin ivmesi de radyal ve teğet bileşenlere ayrılabilir. İvme, hızın zamana göre türevidir:

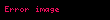




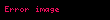
Negatif işaret 
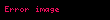

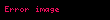
Merkezcil hızlanma yarıçap içine doğru yönlendirilen radyal bileşendir.
Teğet bileşen süratın genliğini değiştirirken:
Karmaşık sayıları kullanma
Dairesel hareket karmaşık sayılar kullanılarak tanımlanabilir. 



reel eksen ile karmaşık vektörün açısıdır ve t süresinin bir fonksiyonudur. Yarıçap sabit olduğundan:
Her bir nokta zaman farklılığını temsil eder. Bu formül ile sürat:
haline gelir.
Ve ivme:
İlk terim yerdeğiştirme vektörüne ters yönde ve ikinci terim daha önceki sonuçlarda gösterildiği gibi dikeydir.
Tartışma
Sürat (.)(.)
Şekil 1 sürat ve ivme vektörlerinin yörüngede dört farklı noktadaki değişmeyen hareketlerini gösteriyor. v vektörü dairesel yola teğet olduğu için, iki vektör hiçbir zaman aynı yöne doğrulmaz. Nesne sabit bir hıza sahip olmasına rağmen, yönü sürekli değişir. Sürattaki bu değişim genliği sabit tutulan (süratin olduğu gibi) fakat yönü sürekli değişen a ivmesinden kaynaklanır. İvme yarıçapın içine doğru (merkezcil olarak) yönelir ve sürate diktir. Bu ivme merkezcil ivme olarak bilinir
Bir r yarıçaplı yol için, bir θ açısı süpürüldüğünde yörünge çevresinde gidilen mesafe s = rθ’dır. Bu yüzden, yörünge etrafında dönüşün hızı:
Rotasyonun açısal değeri ω’dir. (Yeniden düzenleme ile, ω = v/r.) Yani, vdeğişmez ve sürat vektörü v de sabit genlik v ile aynı ω açısal değerinde döner.
Bağıl Dairesel Hareket
Bu durumda üç ivme vektörü üç sürat vektörüne diktir,
Ve bütün referans çerçevelerinde aynı skaler sabit olarak ifade edilen düzgün ivmenin karesine dik,
Dairesel hareketin ifadesi haline gelir.
Ya da pozitif karekökünü alarak ve üç ivmeyi kullanarak, dairesel hareket için uygun ivmeye ulaşırız:
İvme
Şekil 2’deki sol daire iki komşu zamanda sürat vektörlerini gösteren yörüngedir. Sağda, bu iki sürat kuyrukları çarpıştırılmak için hareket ettiriliyor. Hız sabit olduğu için, sağdaki sürat vektörler zaman geçtikçe bir daire oluşturuyor. Bir dθ = ω dt süpürülme açısı için, v’deki değişiklik v’nin sağ açılarında ve v dθ genliğinde bir vektördü, ki bu dolayısıyla ivme genliği şöyle verilmiştir:
Bazı sürat yarıçap ve genlik değerleri için merkezcil ivme
|v| r | 1 m/s 3.6 km/h 2.2 mph | 2 m/s 7.2 km/h 4.5 mph | 5 m/s 18 km/h 11 mph | 10 m/s 36 km/h 22 mph | 20 m/s 72 km/h 45 mph | 50 m/s 180 km/h 110 mph | 100 m/s 360 km/h 220 mph | |
|---|---|---|---|---|---|---|---|---|
| Slow | City car | |||||||
| 10 cm 3.9 in | 10 m/s² 1.0 g | 40 m/s² 4.1 g | 250 m/s² 25 g | 1.0 km/s² 100 g | 4.0 km/s² 410 g | 25 km/s² 2500 g | 100 km/s² 10000 g | |
| 20 cm 7.9 in | 5.0 m/s² 0.51 g | 20 m/s² 2.0 g | 130 m/s² 13 g | 500 m/s² 51 g | 2.0 km/s² 200 g | 13 km/s² 1300 g | 50 km/s² 5100 g | |
| 50 cm 1.6 ft | 2.0 m/s² 0.20 g | 8.0 m/s² 0.82 g | 50 m/s² 5.1 g | 200 m/s² 20 g | 800 m/s² 82 g | 5.0 km/s² 510 g | 20 km/s² 2000 g | |
| 1 m 3.3 ft | carousel | 1.0 m/s² 0.10 g | 4.0 m/s² 0.41 g | 25 m/s² 2.5 g | 100 m/s² 10 g | 400 m/s² 41 g | 2.5 km/s² 250 g | 10 km/s² 1000 g |
| 2 m 6.6 ft | 500 mm/s² 0.051 g | 2.0 m/s² 0.20 g | 13 m/s² 1.3 g | 50 m/s² 5.1 g | 200 m/s² 20 g | 1.3 km/s² 130 g | 5.0 km/s² 510 g | |
| 5 m 16 ft | 200 mm/s² 0.020 g | 800 mm/s² 0.082 g | 5.0 m/s² 0.51 g | 20 m/s² 2.0 g | 80 m/s² 8.2 g | 500 m/s² 51 g | 2.0 km/s² 200 g | |
| 10 m 33 ft | 100 mm/s² 0.010 g | 400 mm/s² 0.041 g | 2.5 m/s² 0.25 g | 10 m/s² 1.0 g | 40 m/s² 4.1 g | 250 m/s² 25 g | 1.0 km/s² 100 g | |
| 20 m 66 ft | 50 mm/s² 0.0051 g | 200 mm/s² 0.020 g | 1.3 m/s² 0.13 g | 5.0 m/s² 0.51 g | 20 m/s² 2 g | 130 m/s² 13 g | 500 m/s² 51 g | |
| 50 m 160 ft | 20 mm/s² 0.0020 g | 80 mm/s² 0.0082 g | 500 mm/s² 0.051 g | 2.0 m/s² 0.20 g | 8.0 m/s² 0.82 g | 50 m/s² 5.1 g | 200 m/s² 20 g | |
| 100 m 330 ft | Freeway | 10 mm/s² 0.0010 g | 40 mm/s² 0.0041 g | 250 mm/s² 0.025 g | 1.0 m/s² 0.10 g | 4.0 m/s² 0.41 g | 25 m/s² 2.5 g | 100 m/s² 10 g |
| 200 m 660 ft | 5.0 mm/s² 0.00051 g | 20 mm/s² 0.0020 g | 130 m/s² 0.013 g | 500 mm/s² 0.051 g | 2.0 m/s² 0.20 g | 13 m/s² 1.3 g | 50 m/s² 5.1 g | |
| 500 m 1600 ft | 2.0 mm/s² 0.00020 g | 8.0 mm/s² 0.00082 g | 50 mm/s² 0.0051 g | 200 mm/s² 0.020 g | 800 mm/s² 0.082 g | 5.0 m/s² 0.51 g | 20 m/s² 2.0 g | |
| 1 km 3300 ft | Yüksek hızlı demiryolu | 1.0 mm/s² 0.00010 g | 4.0 mm/s² 0.00041 g | 25 mm/s² 0.0025 g | 100 mm/s² 0.010 g | 400 mm/s² 0.041 g | 2.5 m/s² 0.25 g | 10 m/s² 1.0 g |
Düzensiz Dairesel Hareket

Düzensiz dairesel hareket dairesel bir yolda hareket eden bir nesnenin sahip olduğu değişken bir hızın olduğu her durumdur. Teğetsel ivme sıfırdan farklıdır; hız değişkendir.
Sıfırdan farklı bir teğetsel ivme olduğu için, kendi merkezcil gücüne (kütle ve radyal ivmeden oluşan) ek olarak, bir nesne üzerine etki eden güçler vardır. Bu güçler ağırlık, normal kuvvet ve sürtünme kuvvetini içerir.

Düzensiz dairesel harekette, normal kuvvet her zaman ağırlığın tersi yöne doğrulmaz. İşte düz bir şekilde hareket eden ve aniden düz bir yola geri atlayan bir nesne görüyorsunuz. Bu diyagram ağırlığın tersi yönden ziyade farklı yönlere doğrulan normal kuvveti gösteriyor. Normal kuvvet aslında ağırlık kuvvetini önlemek ve merkezcil kuvvete katkı sağlamaya yardım eden radyal ve teğet kuvvetlerin toplamıdır. Merkezcil kuvvete katkı sağlayan Normal kuvvetin yatay bileşenidir. Normal kuvvetin dikey bileşeni ise nesnenin ağırlığına karşı koyar.
Düzensiz dairesel harekette normal kuvvet ve ağırlık aynı yöne doğru olabilir. İki kuvvet de aşağıya doğrulabilir fakat nesne aşağıya düşmeden dairesel bir yolda kalacaktır. Öncelikle normal kuvvetin neden ilk olarak aşağıya doğrulacağını görelim. İlk diyagramda, nesnenin bir uçağın içinde oturan bir insan olduğunu varsayalım, iki güç de yalnızca nesne dairenin tepesine ulaştığında aşağıya yöneliyor. Hem ağırlık hem de merkezcil kuvvet dairenin tepesindeyken aşağıya yöneldiğinden, normal kuvvet de aşağıya yönelecektir. Mantıklı bir açıdan, uçakta seyahat eden bir kişi dairenin tepe noktasında tepetaklak olacaktır. O anda, kişinin koltuğu aslında kişi üzerine bastırır ve bu normal kuvvettir

Nesnenin yalnızca aşağıya doğru olan kuvvetlere maruz kaldığında aşağıya düşmeme nedeni basittir. Bir nesneyi fırlatıldıktan sonra havada tutanın ne olduğunu bir düşünün. Bir nesne havaya atıldığı anda, nesne üzerine etki eden aşağıya doğru tek kuvvet yerçekimi kuvvetidir. Bu bir nesne havaya atıldığında hemen yere düşeceği anlamına gelmez. Nesneyi havada tutan şey süratidir. Newton’un hareket yasalarının ilki bir nesnenin eylemsizliği onu hareketli tuttuğunu belirtir ve nesne havadayken bir sürati olduğundan o yönde hareket etmeyi sürdürmeye eğilim gösterir.
Uygulamalar
Düzensiz dairesel hareket ile ilgili çözüm uygulamaları kuvvet analizlerini içerir. Düzgün dairesel hareketle, bir dairede hareket eden nesne üzerine etki eden tek kuvvet merkezcil kuvvettir. Düzensiz dairesel harekette, sıfırdan farklı bir teğetsel ivmeden dolayı nesne üzerine etkiyen ek kuvvetler vardır. Ek kuvvetler olmasına rağmen, nesne üzerine etki eden bütün kuvvetlerin toplamı merkezcil kuvvete eşit olmak zorundadır.


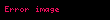
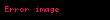
Radyal ivme total kuvvet hesaplanırken kullanılır. Teğetsel ivme nesneyi bir dairesel yolda tutmaktan sorumlu olmadığı için hesaplamada kullanılmaz. Nesneyi dairede hareket halinde tutan tek ivme radyal ivmedir. Bütün kuvvetlerin toplamı merkezcil kuvvet olduğu için, merkezcil kuvveti serbest cisim diyagramına çizmek gerekli değildir ve genellikle önerilmez.
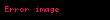
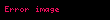

Düzgün dairesel harekette, dairesel yoldaki bir nesnenin total ivmesi radyal ivmeye eşittir. Düzensiz dairesel harekette teğetsel ivme var olduğundan, bu geçerli olmuyor. Düzensiz dairesel harekette bir nesnenin total ivmesini bulmak için, radyal ve teğetsel ivmenin toplam vektörünü bulun.

Radyal ivme yine 

wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte dairesel hareket bir nesnenin dairesel bir yorunge boyunca bir rotasyon ya da cemberin cevresinde yaptigi harekettir Rotasyonun ve surekli hizin surekli acisal degeriyle birlikte duzgun ya da degisen rotasyon degeriyle duzensiz olabilir 3 boyutlu bir cismin sabit ekseni etrafindaki rotasyon parcalarinin dairesel hareketini icerir Hareketin denkligi bir cisim kutlesinin merkezini tanimlar Dairesel hareketin ornekleri sunlari icerir sabit agirlikta Dunya yorungesinde donen yapay bir uydu bir ipe baglanmis ve daireler seklinde sallanan bir tas parkurda viraj boyunca donen bir araba duzgun bir manyetik alana dikey olarak hareket eden bir elektron ve bir mekanizmanin icerisinde donen bir disli Nesnenin surat vektoru surekli yon degistirdigi icin hareket eden nesne rotasyon merkezinin yondeki merkezcil bir kuvvet tarafindan ivme kazandiriliyor Newton un hareket yasalarina gore bu ivme olmadan nesne duz bir cizgide hareket eder UniformFigure 1 Velocity v and acceleration a in uniform circular motion at angular rate w the speed is constant but the velocity is always tangent to the orbit the acceleration has constant magnitude but always points toward the center of rotationFigure 2 The velocity vectors at time t and time t dt are moved from the orbit on the left to new positions where their tails coincide on the right Because the velocity is fixed in magnitude at v r w the velocity vectors also sweep out a circular path at angular rate w As dt 0 the acceleration vector a becomes perpendicular to v which means it points toward the center of the orbit in the circle on the left Angle w dt is the very small angle between the two velocities and tends to zero as dt 0Figure 3 Left Ball in circular motion rope provides centripetal force to keep ball in circle Right Rope is cut and ball continues in straight line with velocity at the time of cutting the rope in accord with Newton s law of inertia because centripetal force is no longer there Fizikte duzgun dairesel hareket dairesel bir yorungeyi sabit suratle gecen bir cismin hareketini tanimlar Cisminin rotasyon ekseninden uzakligi her zaman sabit kalir Cismin suratinin sabit olmasina ragmen hizi sabit degildir hiz vektorel bir buyukluk hem cismin suratine hem gidis yonune baglidir Bu degisken hiz bir ivmenin varligini gosterir bu merkezcil ivme duzgun genlikten kaynaklanir ve her zaman rotasyon eksenine dogru yonlendirilir Bu ivme dolayisiyla ayni sekilde genlikte duzgun ve rotasyon eksenine dogru yonlendirilmis merkezcil bir guc tarafindan uretilir Yorungenin yaricapina oranla goz ardi edilebilecek kucuklukte olmayan sert bir cismin sabit ekseni etrafindaki rotasyon durumunda cismin her bir parcacigi ayni acisal surat fakat konum ve yorungeye bagli olarak degisen surat ve ivmeli bir duzgun dairesel hareket tanimlar FormullerFigure 1 Vector relationships for uniform circular motion vector W representing the rotation is normal to the plane of the orbit r yaricapli bir dairede hareket icin dairenin cevresi C 2p r dir Bir tam donus icin periyot T ayni zamanda acisal surat olarak bilinen rotasyonun acisal degeri ise w w 2pT displaystyle omega frac 2 pi T Ve birimler radyan saniye dir Daireyi dolasan nesnenin hizi v 2prT wr displaystyle v frac 2 pi r T omega r T surede supurulen 8 acisi 8 2ptT wt displaystyle theta 2 pi frac t T omega t Yondeki degisiklikten kaynaklanan ivme a v2r w2r displaystyle a frac v 2 r omega 2 r Vektorel iliskiler Sekil 1 de gosteriliyor Rotasyon ekseni w d8 dt genligiyle ve yorunge duzlemine dik W vektoru olarak gosterilmistir W vektorunun yonu sag el kurali kullanilarak bulunmustur Rotasyon belirlemek icin olan bu kuralla surat vektor carpi urun olarak verilir F burada vektor hem W hem de r t ye dikey yorungeye teget ve w r genligindedir Ayni sekilde ivme a W v W W r displaystyle mathbf a boldsymbol Omega times mathbf v boldsymbol Omega times left boldsymbol Omega times mathbf r right olarak verilir burada vektor w v w2r genliginde hem W hem de v t ye dikeydir ve r t nin tam ziddi yone dogrultulmustur En basit olarak hiz kutle ve yaricap sabittir Bir kilogramlik bir cismin saniyede bir radyanin acisal suratiyle bir metre yaricap etrafinda dairesel olarak hareket ettigini varsayalim Hiz saniyede 1 metredir Iceriye dogru ivme 1 m s2 dir 1 m s2 de 1 kilogram merkezcil guce baglidir ve bu bir newton eder Cismin momentumu 1 kg m s 1 dir Eylemsizlik momentumu 1 kg m dir Acisal momentumu 1 kg m s 1 dir Kinetik enerji jouledur Yorungenin cevresi 2p 6 283 metredir Hareketin devri donus basinda 2p saniyedir Frekans 2p 1 hertz dir Kutupsal KoordinatlarFigure 2 Polar coordinates for circular trajectory On the left is a unit circle showing the changes du R displaystyle mathbf d hat u R and du 8 displaystyle mathbf d hat u theta in the unit vectors u R displaystyle mathbf hat u R and u 8 displaystyle mathbf hat u theta for a small increment d8 displaystyle mathrm d theta in angle 8 displaystyle mathrm theta Dairesel hareket boyunca cisim herhangi bir referans yonden konumlandirilmis 8 t acisinda orijin olarak alinan yorungenin merkezinden R sabit uzakligi olan kutupsal koordinat sistemi olarak tanimlanabilecek bir egride hareket eder Bakiniz Sekil 2 r displaystyle stackrel vec r vektorunun yer degisimi orijinden parcacik konumuna olan radyal vektordur r Ru R t displaystyle vec r R hat u R t u R t displaystyle hat u R t t suresinde orijinden uzaklasan radyal vektore paralel birim vektorun oldugu yerdir Ortogonal birim vektoru u R displaystyle hat u R olarak da adlandirilan u 8 displaystyle hat u theta ye gostermek icin uygun bir noktadir u 8 displaystyle hat u theta yi yorunge boyu dolasim yonune dogrultmak icin musaittir Hiz yerdegisimin zamana gore turevidir v ddtr t dRdtu R Rdu Rdt displaystyle vec v frac d dt vec r t frac dR dt hat u R R frac d hat u R dt Dairenin yaricapi sabit oldugundan hizin radyal bileseni sifirdir u R displaystyle hat u R birim vektoru degismez zamanli birlesme genligine sahiptir boylece sure degistikce ucu daima r t displaystyle vec r t ile ayni acida olan 8 acisiyla birim yaricapin dairesinde uzanir Eger parcacik yerdegisimi dt surede d8 acisiyla donerse d8 genligindeki birim daire uzerinde bir yay tanimlayan u R displaystyle hat u R de doner Bakiniz Sekil 2 deki solda birim daire Bu yuzden du Rdt d8dtu 8 displaystyle frac d hat u R dt frac d theta dt hat u theta Degisimin yonu u R displaystyle hat u R ye dikey diger bir deyisle u 8 displaystyle hat u theta boyunca olmalidir cunku u R displaystyle hat u R yonunde du R displaystyle hat u R deki herhangi bir degisim u R displaystyle hat u R nin buyuklugunu degistirecektir Isaret pozitif cunku d8 daki artis nesne ve u R displaystyle hat u R nin u 8 displaystyle hat u theta yonunde hareket ettiklerini gosteriyor Bu yuzden hiz v ddtr t Rdu Rdt Rd8dtu 8 Rwu 8 displaystyle vec v frac d dt vec r t R frac d hat u R dt R frac d theta dt hat u theta R omega hat u theta haline geliyor Cismin ivmesi de radyal ve teget bilesenlere ayrilabilir Ivme hizin zamana gore turevidir a ddtv ddt R w u 8 displaystyle vec a frac d dt vec v frac d dt left R omega hat u theta right R dwdt u 8 w du 8dt displaystyle R left frac d omega dt hat u theta omega frac d hat u theta dt right dd u 8 displaystyle hat u theta nin zamana gore turevi u R displaystyle hat u R icin olan ayni yontemle bulunur Yine u 8 displaystyle hat u theta bir birim vektordur ve ucu p 2 8 acili bir birim daireyi takip eder Dolayisiyla r t displaystyle vec r t ile d8 acisindaki bir artis u 8 displaystyle hat u theta nin d8 genliginde bir yayi izledigini gosterir ve u 8 displaystyle hat u theta u R displaystyle hat u R ye ortogontal oldugu icin du 8dt d8dtu R wu R displaystyle frac d hat u theta dt frac d theta dt hat u R omega hat u R Negatif isaret u 8 displaystyle hat u theta yi u R displaystyle hat u R ye otogonal tutmak icin zorunlu Aksi takdirde u 8 displaystyle hat u theta ve u R displaystyle hat u R arasindaki aci d8 daki artisla birlikte azalacakti Bakiniz Sekil 2 solda birim daire Sonuc olarak ivme a R dwdt u 8 w du 8dt displaystyle vec a R left frac d omega dt hat u theta omega frac d hat u theta dt right Rdwdt u 8 w2R u R displaystyle R frac d omega dt hat u theta omega 2 R hat u R dd Merkezcil hizlanma yaricap icine dogru yonlendirilen radyal bilesendir a R w2Ru R displaystyle vec a R omega 2 R hat u R Teget bilesen suratin genligini degistirirken a 8 Rdwdt u 8 dRwdt u 8 d v dt u 8 displaystyle vec a theta R frac d omega dt hat u theta frac dR omega dt hat u theta frac d vec v dt hat u theta Karmasik sayilari kullanmaDairesel hareket karmasik sayilar kullanilarak tanimlanabilir x displaystyle x ekseni reel eksen ve y displaystyle y ekseni sanal eksen olsun Cismin konumu bu durumda z displaystyle z karmasik vektor olarak verilebilir z x iy R cos 8 isin 8 Rei8 displaystyle z x iy R cos theta i sin theta Re i theta i displaystyle i sanal birim ve 8 8 t displaystyle theta theta t reel eksen ile karmasik vektorun acisidir ve t suresinin bir fonksiyonudur Yaricap sabit oldugundan R R 0 displaystyle dot R ddot R 0 Her bir nokta zaman farkliligini temsil eder Bu formul ile surat v z d Rei8 dt Rd8dtd ei8 d8 iR8 ei8 iw Rei8 iwz displaystyle v dot z frac d Re i theta dt R frac d theta dt frac d e i theta d theta iR dot theta e i theta i omega cdot Re i theta i omega z haline gelir Ve ivme a v iw z iwz iw w2 z displaystyle a dot v i dot omega z i omega dot z i dot omega omega 2 z iw w2 Rei8 displaystyle left i dot omega omega 2 right Re i theta w2Rei8 w eip2Rei8 displaystyle omega 2 Re i theta dot omega e i frac pi 2 Re i theta dd Ilk terim yerdegistirme vektorune ters yonde ve ikinci terim daha onceki sonuclarda gosterildigi gibi dikeydir TartismaSurat Sekil 1 surat ve ivme vektorlerinin yorungede dort farkli noktadaki degismeyen hareketlerini gosteriyor v vektoru dairesel yola teget oldugu icin iki vektor hicbir zaman ayni yone dogrulmaz Nesne sabit bir hiza sahip olmasina ragmen yonu surekli degisir Surattaki bu degisim genligi sabit tutulan suratin oldugu gibi fakat yonu surekli degisen a ivmesinden kaynaklanir Ivme yaricapin icine dogru merkezcil olarak yonelir ve surate diktir Bu ivme merkezcil ivme olarak bilinir Bir r yaricapli yol icin bir 8 acisi supuruldugunde yorunge cevresinde gidilen mesafe s r8 dir Bu yuzden yorunge etrafinda donusun hizi v rd8dt rw displaystyle v r frac d theta dt r omega Rotasyonun acisal degeri w dir Yeniden duzenleme ile w v r Yani vdegismez ve surat vektoru v de sabit genlik v ile ayni w acisal degerinde doner Bagil Dairesel HareketBu durumda uc ivme vektoru uc surat vektorune diktir u a 0 displaystyle vec u cdot vec a 0 Ve butun referans cercevelerinde ayni skaler sabit olarak ifade edilen duzgun ivmenin karesine dik a2 g4a2 g6 u a 2 displaystyle alpha 2 gamma 4 a 2 gamma 6 vec u cdot vec a 2 Dairesel hareketin ifadesi haline gelir a2 g4a2 displaystyle alpha 2 gamma 4 a 2 Ya da pozitif karekokunu alarak ve uc ivmeyi kullanarak dairesel hareket icin uygun ivmeye ulasiriz a g2v2r displaystyle alpha gamma 2 frac v 2 r IvmeSekil 2 deki sol daire iki komsu zamanda surat vektorlerini gosteren yorungedir Sagda bu iki surat kuyruklari carpistirilmak icin hareket ettiriliyor Hiz sabit oldugu icin sagdaki surat vektorler zaman gectikce bir daire olusturuyor Bir d8 w dt supurulme acisi icin v deki degisiklik v nin sag acilarinda ve v d8 genliginde bir vektordu ki bu dolayisiyla ivme genligi soyle verilmistir a vd8dt vw v2r displaystyle a v frac d theta dt v omega frac v 2 r Bazi surat yaricap ve genlik degerleri icin merkezcil ivme Centripetal acceleration for some values of radius and magnitude of velocity v r 1 m s 3 6 km h 2 2 mph 2 m s 7 2 km h 4 5 mph 5 m s 18 km h 11 mph 10 m s 36 km h 22 mph 20 m s 72 km h 45 mph 50 m s 180 km h 110 mph 100 m s 360 km h 220 mphSlow City car10 cm 3 9 in 10 m s 1 0 g 40 m s 4 1 g 250 m s 25 g 1 0 km s 100 g 4 0 km s 410 g 25 km s 2500 g 100 km s 10000 g20 cm 7 9 in 5 0 m s 0 51 g 20 m s 2 0 g 130 m s 13 g 500 m s 51 g 2 0 km s 200 g 13 km s 1300 g 50 km s 5100 g50 cm 1 6 ft 2 0 m s 0 20 g 8 0 m s 0 82 g 50 m s 5 1 g 200 m s 20 g 800 m s 82 g 5 0 km s 510 g 20 km s 2000 g1 m 3 3 ft carousel 1 0 m s 0 10 g 4 0 m s 0 41 g 25 m s 2 5 g 100 m s 10 g 400 m s 41 g 2 5 km s 250 g 10 km s 1000 g2 m 6 6 ft 500 mm s 0 051 g 2 0 m s 0 20 g 13 m s 1 3 g 50 m s 5 1 g 200 m s 20 g 1 3 km s 130 g 5 0 km s 510 g5 m 16 ft 200 mm s 0 020 g 800 mm s 0 082 g 5 0 m s 0 51 g 20 m s 2 0 g 80 m s 8 2 g 500 m s 51 g 2 0 km s 200 g10 m 33 ft 100 mm s 0 010 g 400 mm s 0 041 g 2 5 m s 0 25 g 10 m s 1 0 g 40 m s 4 1 g 250 m s 25 g 1 0 km s 100 g20 m 66 ft 50 mm s 0 0051 g 200 mm s 0 020 g 1 3 m s 0 13 g 5 0 m s 0 51 g 20 m s 2 g 130 m s 13 g 500 m s 51 g50 m 160 ft 20 mm s 0 0020 g 80 mm s 0 0082 g 500 mm s 0 051 g 2 0 m s 0 20 g 8 0 m s 0 82 g 50 m s 5 1 g 200 m s 20 g100 m 330 ft Freeway 10 mm s 0 0010 g 40 mm s 0 0041 g 250 mm s 0 025 g 1 0 m s 0 10 g 4 0 m s 0 41 g 25 m s 2 5 g 100 m s 10 g200 m 660 ft 5 0 mm s 0 00051 g 20 mm s 0 0020 g 130 m s 0 013 g 500 mm s 0 051 g 2 0 m s 0 20 g 13 m s 1 3 g 50 m s 5 1 g500 m 1600 ft 2 0 mm s 0 00020 g 8 0 mm s 0 00082 g 50 mm s 0 0051 g 200 mm s 0 020 g 800 mm s 0 082 g 5 0 m s 0 51 g 20 m s 2 0 g1 km 3300 ft Yuksek hizli demiryolu 1 0 mm s 0 00010 g 4 0 mm s 0 00041 g 25 mm s 0 0025 g 100 mm s 0 010 g 400 mm s 0 041 g 2 5 m s 0 25 g 10 m s 1 0 gDuzensiz Dairesel HareketDuzensiz dairesel hareket dairesel bir yolda hareket eden bir nesnenin sahip oldugu degisken bir hizin oldugu her durumdur Tegetsel ivme sifirdan farklidir hiz degiskendir Sifirdan farkli bir tegetsel ivme oldugu icin kendi merkezcil gucune kutle ve radyal ivmeden olusan ek olarak bir nesne uzerine etki eden gucler vardir Bu gucler agirlik normal kuvvet ve surtunme kuvvetini icerir Duzensiz dairesel harekette normal kuvvet her zaman agirligin tersi yone dogrulmaz Iste duz bir sekilde hareket eden ve aniden duz bir yola geri atlayan bir nesne goruyorsunuz Bu diyagram agirligin tersi yonden ziyade farkli yonlere dogrulan normal kuvveti gosteriyor Normal kuvvet aslinda agirlik kuvvetini onlemek ve merkezcil kuvvete katki saglamaya yardim eden radyal ve teget kuvvetlerin toplamidir Merkezcil kuvvete katki saglayan Normal kuvvetin yatay bilesenidir Normal kuvvetin dikey bileseni ise nesnenin agirligina karsi koyar Duzensiz dairesel harekette normal kuvvet ve agirlik ayni yone dogru olabilir Iki kuvvet de asagiya dogrulabilir fakat nesne asagiya dusmeden dairesel bir yolda kalacaktir Oncelikle normal kuvvetin neden ilk olarak asagiya dogrulacagini gorelim Ilk diyagramda nesnenin bir ucagin icinde oturan bir insan oldugunu varsayalim iki guc de yalnizca nesne dairenin tepesine ulastiginda asagiya yoneliyor Hem agirlik hem de merkezcil kuvvet dairenin tepesindeyken asagiya yoneldiginden normal kuvvet de asagiya yonelecektir Mantikli bir acidan ucakta seyahat eden bir kisi dairenin tepe noktasinda tepetaklak olacaktir O anda kisinin koltugu aslinda kisi uzerine bastirir ve bu normal kuvvettir Nesnenin yalnizca asagiya dogru olan kuvvetlere maruz kaldiginda asagiya dusmeme nedeni basittir Bir nesneyi firlatildiktan sonra havada tutanin ne oldugunu bir dusunun Bir nesne havaya atildigi anda nesne uzerine etki eden asagiya dogru tek kuvvet yercekimi kuvvetidir Bu bir nesne havaya atildiginda hemen yere dusecegi anlamina gelmez Nesneyi havada tutan sey suratidir Newton un hareket yasalarinin ilki bir nesnenin eylemsizligi onu hareketli tuttugunu belirtir ve nesne havadayken bir surati oldugundan o yonde hareket etmeyi surdurmeye egilim gosterir UygulamalarDuzensiz dairesel hareket ile ilgili cozum uygulamalari kuvvet analizlerini icerir Duzgun dairesel hareketle bir dairede hareket eden nesne uzerine etki eden tek kuvvet merkezcil kuvvettir Duzensiz dairesel harekette sifirdan farkli bir tegetsel ivmeden dolayi nesne uzerine etkiyen ek kuvvetler vardir Ek kuvvetler olmasina ragmen nesne uzerine etki eden butun kuvvetlerin toplami merkezcil kuvvete esit olmak zorundadir Fnet ma displaystyle F net ma Fnet mar displaystyle F net ma r Fnet mv2 r displaystyle F net mv 2 r Fnet Fc displaystyle F net F c Radyal ivme total kuvvet hesaplanirken kullanilir Tegetsel ivme nesneyi bir dairesel yolda tutmaktan sorumlu olmadigi icin hesaplamada kullanilmaz Nesneyi dairede hareket halinde tutan tek ivme radyal ivmedir Butun kuvvetlerin toplami merkezcil kuvvet oldugu icin merkezcil kuvveti serbest cisim diyagramina cizmek gerekli degildir ve genellikle onerilmez Fnet Fc displaystyle F net F c yi kullanarak cisme etki eden ve Fc displaystyle F c ye esit kilan butun kuvvetleri listelemek icin serbest cisim diyagramlari cizebiliriz Daha sonra bilinmeyenin ne oldugunu bu bir kutle surat egrilme yaricapi surtunme katsayisi normal kuvvet vb olabilir cozebiliriz Ornegin yukaridaki bir yarim dairenin tepe noktasindaki nesneyi gosteren gorsel Fc n mg displaystyle F c n mg olarak ifade edilebilir Duzgun dairesel harekette dairesel yoldaki bir nesnenin total ivmesi radyal ivmeye esittir Duzensiz dairesel harekette tegetsel ivme var oldugundan bu gecerli olmuyor Duzensiz dairesel harekette bir nesnenin total ivmesini bulmak icin radyal ve tegetsel ivmenin toplam vektorunu bulun ar2 at2 a displaystyle sqrt a r 2 a t 2 a Radyal ivme yine v2 r displaystyle v 2 r ye esittir Tegetsel ivme basit olarak verilen herhangi bir noktada suratin turevidir at dv dt displaystyle a t dv dt Bu ayri radyal ve tegetsel ivmelerin karelerinin toplami koku yalnizca dairesel hareket icin dogrudur bu durumda radyal ivme ar v2 r d2r dt2 displaystyle a r v 2 r d 2 r dt 2 oldugu icin polar koordinatlarla r 8 displaystyle r theta bir ucak icindeki genel hareket icin Coriolis terimi ac 2 dr dt d8 dt displaystyle a c 2 dr dt d theta dt at displaystyle a t ye eklenmelidir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State