Bu maddedeki bilgilerin için ek kaynaklar gerekli. (Ekim 2019) () |
Esnek çarpışma ya da elastik çarpışma, iki cismin arasındaki esnek çarpışma, toplam momentum ve toplam kinetik enerjinin çarpışmadan önce ve sonra sabit kaldığı çarpışmadır. Bilardo topu çarpışmaları ve herhangi bir sıcaklıkta hava moleküllerinin duvarla çarpışması yaklaşık olarak esnektir. Gerçek esnek çarpışmalar, atom ve atom-altı parçacıklar arasında gerçekleşir. Esnek çarpışmalar sadece diğer formlara dönüşen net kinetik enerji yoksa gerçekleşir.

Küçük cisimlerin çarpışmaları sırasında, kinetik enerji ilk olarak parçacıklar arasında olan itici kuvvet ile ilgili olan potansiyel enerjiye dönüşür. (parçacıklar bu kuvvete karşı hareket ederken, kuvvet ve bağıl hız arasındaki açı geniştir). Ve daha sonra potansiyel enerji tekrar kinetik enerjiye dönüşür. (parçacıklar bu kuvvete karşı hareket ederken, kuvvet ve bağıl hız arasındaki açı dardır).
Atomlar arasında olan çarpışmalar esnek çarpışmalardır. Rutherford’un geri saçılması deneyi bunun bir örneğidir.
Atomları arasındaki mesafe daha fazla olan moleküllerden gazlar ve sıvılarda mükemmel esnek çarpışma meydana gelir, çünkü her çarpışmayla birlikte moleküllerin içinde ve öteleme hareketleri arasında kinetik enerji değişimi yaşanır. Herhangi bir anda, çarpışmaların yarı yarıya değişen oranında; bir yarısı esnek olmayan çarpışma (çarpışma öncesi sahip olduğu kinetik enerjiye nazaran çarpışma sonrasında daha az kinetik enerjiye sahip olan çarpışmalar) ve diğer yarısı da mükemmel derecede esnek olan çarpışmalar (çarpışma öncesi sahip olduğu kinetik enerji kadar çarpışma sonrasında da aynı kinetik enerjiye sahip olan çarpışmalar) olur. Tüm örnekler karşılaştırıldığında ortalama olarak, Planck’s yasası sistemden enerji taşımak için siyah cisim fotonlarını engellediği sürece, moleküler çarpışmalar esnek çarpışmalar olarak düşünülebilir.
Makroskopik cisimlerin durumunda, mükemmel esnek olan çarpışmalar asla tamamen fark edilmeyecek kadar ideal, ama yaklaşık olarak cisimlerin etkileşimi bilardo toplarının etkileşimi kadardır.
Enerji düşünüldüğünde, çarpışmadan önceki dönme enerjisi ve çarpışmadan sonraki dönme enerjisinin rol oynaması da mümkündür.
Denklemler
Bir boyutta Newton denklemleri
1 ve 2 diye gösterilmiş iki tane parçacık düşünüldüğünde. m1 ve m2 cisimlerin kütleleridir, u1 ve u2 cisimlerin çarpışmadan önceki hızlarıdır ve v1 ve v2 cisimlerin çarpışmadan sonraki hızlarıdır.
Toplam momentumun korunumunu çarpışmadan önce ve çarpışmadan sonra aynı olan toplam momentumlara bakarak söyleyebiliriz ve bunu da şu denklemlerle ifade edebiliriz.
Benzer şekilde, toplam kinetik enerjinin korunumunu da çarpışmadan önce ve çarpışmadan sonra aynı olan toplam kinetik enerjilere bakarak söyleyebiliriz ve bunu da şu denklemlerle ifade edebiliriz.
Bu denklemler vi, ui bilindiğinde veya tersi durum söz konusu olduğunda doğrudan çözülebilir. Bir diğer alternatif çözüm yolu ise referans noktasını değiştirmek ve bilinen hızlardan birini sıfır almaktır. Bu yeni referans noktasındaki bilinmeyen hızların değerine daha sonra orijinal referans noktasındaki dönüşüm denklemleriyle ulaşılabilir. Bilinmeyen hızın değeri bir kez saptandığında, diğer hızın değeri simetri yöntemi kullanılarak bulunabilir.
vi için bu eş zamanlı denklemlerin çözümü bize bu denklemleri verir:
ya da
.
İkinci yoldan yapılan önemsiz çözümdür, çünkü henüz hiçbir çarpışmanın meydana gelmediğini belirtir.
Örneğin:
- Top 1: kütlesi = 3 kg, hızı = 4 m/s olsun
- Top 2: kütlesi = 5 kg, hızı = −6 m/s olsun
Çarpışmadan sonra:
- Top 1: hızı = −8.5 m/s olur
- Top 2: hızı = 1.5 m/s olur
Denklem:
Türevi alındığında: Kinetik enerji formülünü kullanarak şu sonuca ulaşırız;
Momentum denklemini tekrar düzenlersek:
Kinetik enerji denklemini momentum denklemine böldüğümüzde:
- bir parçacığın diğerine göre olan bağıl hızı çarpışma sonucunda tersine çevrilir.
- iki parçacık için de çarpışmadan önceki ortalama momentumu çarpışmadan sonraki ortalama momentumuna eşittir.

Beklenildiği üzere, sabit öteleme hızıyla birlikte referans noktası kullanıldığında, bütün hızlara sabit bir değer eklendiğinde çözümün değişmez olduğu görülür.

Kütle merkezinin hızı çarpışmayla birlikte değişmez:
Zamanla kütle merkezi 

, ve
Bundan dolayı, çarpışmadan önce ve çarpışmadan sonra kütle merkezinin hızı:
, ve



Kütle merkezi ile ilgili olarak, her iki hız da çarpışmayla birlikte tersine çevrilir: farklı kütleli parçacıkların durumunda, ağır olan parçacık kütle merkezine doğru yavaşlayarak hareket eder ve geri sıçramalar aynı yavaş hızda olur ve hafif olan parçacık kütle merkezine doğru daha hızlı hareket eder ve geri sıçramalar aynı yüksek hızda olur.
Eğer cisimlerin kütleleri yaklaşık olarak aynıysa, 




Bir nötron moderatörü (aşağı hızlı nötronları yavaşlatan bir ortam, böylece bir zincirleme reaksiyon sürdürme yeteneğine sahip termal nötronlar dönüştürerek) (kolayca nötron absorbe olmayan ek özelliği ile ) Işık çekirdekleri ile atomların bir malzeme dolu olmasının nedeni budur : hafif çekirdeklerde nötron aynı kütleye hakkında sahip .
Bir boyutta relativistik esnek çarpışma
Özel relativiteye göre,
p herhangi bir m kütleli, v hızlı parçacığın momentumudur. c ise ışık hızıdır.
Momentum çerçevesindeki merkezde toplam momentum sıfıra eşit olur.

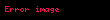

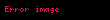
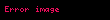





Sistemin toplam enerjisi ve toplam momentumu korunur ve çarpışan cisimlerin geri kalan kütleleri değişmez, çarpışan cisimlerin momentumları çarpışan cisimlerin kütleleriyle, toplam enerji ve toplam momentumlarıyla doğru orantılıdır. Çarpışan cismin momentumunun büyüklüğü çarpışmadan sonra değişmez, ancak hareketinin yönü momentum merkezine göre ters yöndedir.
Klasik fizikteki çok parçacıklı ve yüksek boyutlu sistemler, klasik atomların bir araya gelmesiyle oluşacaklardır. Örneğin hava masası deneylerinde kullanılan diskler üç boyutlu cisimler olmalarına rağmen iki boyuta kısıtlanmış hareketlerinin incelenmesi söz konusu olduğundan iki boyutlu olarak ele alınabilmektedirler. Eğer deneyler yapılırken disklerin kendi simetri eksenleri etrafındaki olası dönmeler (spin hareketleri) engellenebilirse o zaman disklerin hareketleri sadece kütle – merkezlerinin hareketleri ile karakterize edilebileceğinden diskler noktasal parçacıklar olarak düşünülebilirler. Bu dönmelerin kaynakları elektromagnetik kökenli olan sürtünme kuvvetlerinin oluşturduğu torklardır. Hava masasının özelliği, katıların birbirlerine temas ederek hareket etmeleri sırasında var olan şiddetli kinetik sürtünme kuvvetlerini, bunların yanında ihmal edilebilecek büyüklüklere sahip hava sürtünmelerine indirgiyor olmasıdır. Ancak ihmal edilmelerine rağmen var olan bu sürtünme kuvvetlerinden kaynaklanabilecek dönmelerin oluşmaları durumunda deneysel hatalar artacaktır. Dönmelerin söz konusu olduğu (kapalı varsayılabilecek) esnek bir çarpışmada kinetik enerji korunacaktır ancak artık kinetik enerjinin hem öteleme hem de dönmeden kaynaklanan kısımları olacaktır. Klasik noktasal parçacıklar da çarpışırlarken birbirlerine temas etmeyebilirler, örnek olarak biri durgun diğeri de onunla etkileşecek şekilde hareket eden aynı elektrik yüküne sahip noktasal parçacıkların esnek saçılmaları incelenebilir. Böyle bir elektriksel sisteme eşdeğer mekaniksel bir sistem, sadece temas etmek suretiyle etkileştikleri varsayılan iki disk ve onların ötelemesel esnek çarpışmaları ile verilebilir. Klasik Mekanik sadece iyi bir yaklaşımdır. Klasik Mekanik makroskopik boyuttaki cisimlerle ve ışık hızından daha yavaş olan hızlarla uğraştığında bize daha kesin sonuçlar verir. Klasik limitin ötesindeyse, sonuçlar yanlış olur. Momentum merkezinde ve klasik mekaniğe göre, Esnek çarpışma yapan iki cisimli sistemin toplam momentumu momentum referans çerçevesine bağlıdır.

Diğer farklılıklara rağmen göreli hesaplamada doğru kalır. Özel Görelilik içinde önermelerden biri Fizik Kanunlarının tüm atalet çerçeveleri referansında değişmez olması gerektiğini belirtiyor.
Yani, toplam momentum belirli referans çerçevesinde korunursa, toplam momentumun miktarı çerçeveye bağlı olmasına rağmen toplam momentum herhangi bir referans çerçevesinde de korunur. Bu yüzden, bir çerçeveden diğer referans çerçevesine ya da diğerine dönüştürülerek, istenilen sonuçları almak mümkündür. Belli bir referans çerçevesinde, toplam momentum herhangi bir yerde olabilir,
İkili şekilde hareket eden cisimlerin toplam momentumlarına baktığımızda 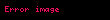



Ve şimdi de momentum merkezindeki çarpışmadan önceki hızlarına bakacak olursak eğer 

and
,
≈
≈
≈
≈
≈
≈
≈
≈
≈
≈
Bu yüzden, çarpışan iki cismin hızı da ışık hızından (yani yaklaşık olarak 300 milyon m/s) çok çok çok düşük olduğunda, klasik hesaplama yöntemi için bu sonuçlar doğrudur.
Çarpışma için başka relativistik türetilmiş formüller
Hızın parametresi olarak adlandırılan parametreden söz etmiştik 
bundan dolayı şu formülü elde ederiz:
Relativistik enerji ve momentum şu şekilde açıklanabilir:
Çarpışan kütlelerin enerji toplamları için denklemler ve çarpışan kütlelerin momentum toplamları için denklemler ise şöyle 









ve birbirine bağlı denklemler, yukarıdaki denklemin toplamı:
denklemin her iki tarafının karesinden de enerjiden momentum çıkarılır ve şu tanım kullanılır 
kütlesi sıfır olmayan cisimler için, şu formülleri elde ederiz:

son denklemden, bir değere sahip çözüm elde ederiz ve şunu çözeriz 


Problemin çözümü bu şekilde, ama hız parametreleriyle açıklanır. Hız parametreleri için yer değiştirme formülleri uygulandığında
Bir önceki adım uygulandığında da bu formül elde edilir: 


İki boyutta esnek çarpışma
Bir - boyutlu esnek çarpışmaların dışındaki esnek çarpışmalarda sadece momentumun ve kinetik enerjinin korunumu çarpışma sonrası hızları belirlemeye yetmeyecektir. Mesela, iki – boyutlu esnek çarpışma durumunda iki parçacık için çarpışma sonrası iki hız ve her hızın iki bileşeni olduğundan dört tane bilinmeyen vardır. Bu dört bilinmeyen, momentumun korunumu nedeniyle iki ve kinetik enerjinin korunumu nedeniyle de bir toplam üç tane skaler denklem ile kısıtlanırlar, ancak son hızların bulunması için fazladan bir bilgiye ihtiyaç duyulmaktadır. Bu bilgiye deney ile ulaşılabilir ve çoğu zaman çarpışma sonrası parçacıklardan birinin ilerleme yönünün (probleme adapte edilmiş) eksenlerden biriyle yaptığı açı (saçılma açısı) bu bilgi için kullanılır.
İki boyutta iki çarpışan cisimlerin her durumunda, her cismin hızı için iki dikey hız bölünmesi gerekir : Bir teğet çarpışan cisimlerin sık görülen normal yüzeylerine temas noktasında, diğeri de bir çarpışma hattı boyunca . Çarpışma sadece çarpma hattı boyunca kuvvet oluşturduğu için, çarpışma noktasına teğet olan hızları değişmez. Çarpışma hattı boyunca hızlar da tek boyutlu bir çarpışma ile aynı denklemler de kullanılabilir . Son hızlar daha sonra iki yeni bileşen hızları hesaplanabilir ve çarpışma noktasına bağlıdır.

Herhangi bir zamanda momentum çerçevesinin merkezinde iki organlarının hızları kitlelere ters orantılı büyüklüklerde, ters yönlerde bulunmaktadır. Esnek çarpışmada bu büyüklükleri değişmez. Uzaklık cisimlerin şekil ve çarpma noktasına bağlı olarak değişebilir . Örneğin, küreler halinde açısı iki gövde merkezlerinin (paralel) yolları arasındaki uzaklığa bağlıdır . Yönü sıfır olmayan herhangi bir değişiklik mümkündür: Bu mesafe hızları çarpışma tersine sıfır ise ; kürelerin yarıçapları toplamı yakın ise iki cisim sadece biraz saptırılır.
İkinci parçacığın çarpışmadan önce hareketsiz olduğunu varsayarsak, iki parçacığın sapma açısı, 


Çarpışmadan sonraki parçacıkların hızlarının büyüklükleri:
İki boyutta iki cisimli çarpışma
İlk topun x ve y son hız bileşenleri şu şekilde hesaplanabilir :
v1 and v2 cisimlerin orijinal hızlarının skalar boyutları, m1 and m2 are their masses, θ1 and θ2 ve hareket açıları, yani, 
Bu denklem iki cisim arasındaki etkileşimi kolayca temas açısı paralel olacak şekilde x ve y ekseni ile tek boyutlu olarak hesaplanabilir ve ayrıca nesnelerin hızlarını da kolay bir şekilde hesaplamaya yarar, yani temas açısı boyunca hesaplanan türetilmiş bir büyüklüktür ve nesneler daha sonra gerçek x ve y bileşenlerini hızlarını almak için geri özgün yönüne döndürülür .
Bir serbest açı gösteriminde, değişen hızlar merkez kullanılarak hesaplanır x1 ve x2
açılı ayraçlar iki vektörün iç çarpımını ve skaler çarpımını gösterirler.
Ayrıca bakınız
Kaynakça
- ^ Landau; Lifshitz, E. M. (1976). Mechanics (3.3ad1=L. D. bas.). Pergamon Press. s. 46. ISBN .
- ^ Craver, William E. "Elastic Collisions." Williamecraver.wix.com. Wix.com, 13 Aug. 2013. Web. 13 Aug. 2013. <http://williamecraver.wix.com/elastic-equations 24 Aralık 2015 tarihinde Wayback Machine sitesinde .>.
- Raymond, David J. "10.4.1 Elastic collisions". A radically modern approach to introductory physics: Volume 1: Fundamental principles. Socorro, NM: New Mexico Tech Press. ISBN .
Dış bağlantılar
- Rigid Body Collision Resolution in three dimensions 6 Ocak 2016 tarihinde Wayback Machine sitesinde . including a derivation using the conservation laws
- VNE Rigid Body Collision Simulation27 Ekim 2010 tarihinde Wayback Machine sitesinde . Small Open Source 3D engine with easy-to-understand implementation of elastic collisions in C
- Visualize 2-D Collision 24 Aralık 2015 tarihinde Wayback Machine sitesinde . Free simulation of 2-particle collision with user-adjustable coefficient of restitution and particle velocities (Requires Adobe Shockwave)
- 2-Dimensional Elastic Collisions without Trigonometry 25 Aralık 2015 tarihinde Wayback Machine sitesinde . Explanation of how to calculate 2-dimensional elastic collisions using vectors
- Bouncescope 20 Şubat 2016 tarihinde Wayback Machine sitesinde . Free simulator of elastic collisions of dozens of user-configurable objects
- Managing ball vs ball collision with Flash 24 Aralık 2015 tarihinde Wayback Machine sitesinde . Flash script to manage elastic collisions among any number of spheres
- Elastic collision derivation 14 Şubat 2017 tarihinde Wayback Machine sitesinde .
- Elastic collision formula derivation if one of balls velocity is 0 19 Ocak 2016 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddedeki bilgilerin dogrulanabilmesi icin ek kaynaklar gerekli Lutfen guvenilir kaynaklar ekleyerek maddenin gelistirilmesine yardimci olun Kaynaksiz icerik itiraz konusu olabilir ve kaldirilabilir Kaynak ara Esnek carpisma haber gazete kitap akademik JSTOR Ekim 2019 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Esnek carpisma ya da elastik carpisma iki cismin arasindaki esnek carpisma toplam momentum ve toplam kinetik enerjinin carpismadan once ve sonra sabit kaldigi carpismadir Bilardo topu carpismalari ve herhangi bir sicaklikta hava molekullerinin duvarla carpismasi yaklasik olarak esnektir Gercek esnek carpismalar atom ve atom alti parcaciklar arasinda gerceklesir Esnek carpismalar sadece diger formlara donusen net kinetik enerji yoksa gerceklesir Kara cisim isimasi gosterilmemis bir sistemden kacamaz termal ajitasyondaki atomlar ozellikle esnek carpisma yaparlar Ortalama olarak iki atom birbirlerine esnek bir sekilde carptiklarinda carpisma oncesinde ve sonrasinda kinetik enerjiler birbirine esittir Bes atom hareketleri daha kolay gorulsun diye kirmizi ile boyandi Kucuk cisimlerin carpismalari sirasinda kinetik enerji ilk olarak parcaciklar arasinda olan itici kuvvet ile ilgili olan potansiyel enerjiye donusur parcaciklar bu kuvvete karsi hareket ederken kuvvet ve bagil hiz arasindaki aci genistir Ve daha sonra potansiyel enerji tekrar kinetik enerjiye donusur parcaciklar bu kuvvete karsi hareket ederken kuvvet ve bagil hiz arasindaki aci dardir Atomlar arasinda olan carpismalar esnek carpismalardir Rutherford un geri sacilmasi deneyi bunun bir ornegidir Atomlari arasindaki mesafe daha fazla olan molekullerden gazlar ve sivilarda mukemmel esnek carpisma meydana gelir cunku her carpismayla birlikte molekullerin icinde ve oteleme hareketleri arasinda kinetik enerji degisimi yasanir Herhangi bir anda carpismalarin yari yariya degisen oraninda bir yarisi esnek olmayan carpisma carpisma oncesi sahip oldugu kinetik enerjiye nazaran carpisma sonrasinda daha az kinetik enerjiye sahip olan carpismalar ve diger yarisi da mukemmel derecede esnek olan carpismalar carpisma oncesi sahip oldugu kinetik enerji kadar carpisma sonrasinda da ayni kinetik enerjiye sahip olan carpismalar olur Tum ornekler karsilastirildiginda ortalama olarak Planck s yasasi sistemden enerji tasimak icin siyah cisim fotonlarini engelledigi surece molekuler carpismalar esnek carpismalar olarak dusunulebilir Makroskopik cisimlerin durumunda mukemmel esnek olan carpismalar asla tamamen fark edilmeyecek kadar ideal ama yaklasik olarak cisimlerin etkilesimi bilardo toplarinin etkilesimi kadardir Enerji dusunuldugunde carpismadan onceki donme enerjisi ve carpismadan sonraki donme enerjisinin rol oynamasi da mumkundur DenklemlerBir boyutta Newton denklemleri source source source source track Profesor Walter Lewin bir boyutta olan esnek carpismalari anlatirken 1 ve 2 diye gosterilmis iki tane parcacik dusunuldugunde m1 ve m2 cisimlerin kutleleridir u1 ve u2 cisimlerin carpismadan onceki hizlaridir ve v1 ve v2 cisimlerin carpismadan sonraki hizlaridir Toplam momentumun korunumunu carpismadan once ve carpismadan sonra ayni olan toplam momentumlara bakarak soyleyebiliriz ve bunu da su denklemlerle ifade edebiliriz m1u 1 m2u 2 m1v 1 m2v 2 displaystyle m 1 vec u 1 m 2 vec u 2 m 1 vec v 1 m 2 vec v 2 Benzer sekilde toplam kinetik enerjinin korunumunu da carpismadan once ve carpismadan sonra ayni olan toplam kinetik enerjilere bakarak soyleyebiliriz ve bunu da su denklemlerle ifade edebiliriz m1u122 m2u222 m1v122 m2v222 displaystyle frac m 1 u 1 2 2 frac m 2 u 2 2 2 frac m 1 v 1 2 2 frac m 2 v 2 2 2 Bu denklemler vi ui bilindiginde veya tersi durum soz konusu oldugunda dogrudan cozulebilir Bir diger alternatif cozum yolu ise referans noktasini degistirmek ve bilinen hizlardan birini sifir almaktir Bu yeni referans noktasindaki bilinmeyen hizlarin degerine daha sonra orijinal referans noktasindaki donusum denklemleriyle ulasilabilir Bilinmeyen hizin degeri bir kez saptandiginda diger hizin degeri simetri yontemi kullanilarak bulunabilir vi icin bu es zamanli denklemlerin cozumu bize bu denklemleri verir v1 u1 m1 m2 2m2u2m1 m2 displaystyle v 1 frac u 1 m 1 m 2 2m 2 u 2 m 1 m 2 v2 u2 m2 m1 2m1u1m1 m2 displaystyle v 2 frac u 2 m 2 m 1 2m 1 u 1 m 1 m 2 ya da v1 u1 displaystyle v 1 u 1 v2 u2 displaystyle v 2 u 2 Ikinci yoldan yapilan onemsiz cozumdur cunku henuz hicbir carpismanin meydana gelmedigini belirtir Ornegin Top 1 kutlesi 3 kg hizi 4 m s olsun Top 2 kutlesi 5 kg hizi 6 m s olsun Carpismadan sonra Top 1 hizi 8 5 m s olur Top 2 hizi 1 5 m s olur Denklem v1 v2 u2 u1 displaystyle v 1 v 2 u 2 u 1 Turevi alindiginda Kinetik enerji formulunu kullanarak su sonuca ulasiriz m1 v12 u12 m2 u22 v22 displaystyle m 1 left v 1 2 u 1 2 right m 2 left u 2 2 v 2 2 right m1 v1 u1 v1 u1 m2 u2 v2 u2 v2 displaystyle Rightarrow m 1 left v 1 u 1 right left v 1 u 1 right m 2 left u 2 v 2 right left u 2 v 2 right Momentum denklemini tekrar duzenlersek m1 v1 u1 m2 u2 v2 displaystyle m 1 v 1 u 1 m 2 u 2 v 2 Kinetik enerji denklemini momentum denklemine boldugumuzde v1 u1 u2 v2 displaystyle v 1 u 1 u 2 v 2 v1 v2 u2 u1 displaystyle Rightarrow v 1 v 2 u 2 u 1 bir parcacigin digerine gore olan bagil hizi carpisma sonucunda tersine cevrilir iki parcacik icin de carpismadan onceki ortalama momentumu carpismadan sonraki ortalama momentumuna esittir Esit kutleli cisimlerin esnek carpismasi Beklenildigi uzere sabit oteleme hiziyla birlikte referans noktasi kullanildiginda butun hizlara sabit bir deger eklendiginde cozumun degismez oldugu gorulur Hareket eden bir referans noktalari sistemindeki cisimlerin esnek carpismasi Kutle merkezinin hizi carpismayla birlikte degismez Zamanla kutle merkezi t displaystyle t carpismadan once ve zamanla t displaystyle t carpismadan sonra bize iki denklem verir x t m1x1 t m2x2 t m1 m2 displaystyle bar x t frac m 1 x 1 t m 2 x 2 t m 1 m 2 ve x t m1x1 t m2x2 t m1 m2 displaystyle bar x t frac m 1 x 1 t m 2 x 2 t m 1 m 2 Bundan dolayi carpismadan once ve carpismadan sonra kutle merkezinin hizi vx m1u1 m2u2m1 m2 displaystyle v bar x frac m 1 u 1 m 2 u 2 m 1 m 2 ve vx m1v1 m2v2m1 m2 displaystyle v bar x frac m 1 v 1 m 2 v 2 m 1 m 2 vx displaystyle v bar x carpismadan onceki toplam momentum ve vx displaystyle v bar x carpismadan sonraki toplam momentum Ve momentum korunur vx vx displaystyle v bar x v bar x Kutle merkezi ile ilgili olarak her iki hiz da carpismayla birlikte tersine cevrilir farkli kutleli parcaciklarin durumunda agir olan parcacik kutle merkezine dogru yavaslayarak hareket eder ve geri sicramalar ayni yavas hizda olur ve hafif olan parcacik kutle merkezine dogru daha hizli hareket eder ve geri sicramalar ayni yuksek hizda olur Eger cisimlerin kutleleri yaklasik olarak ayniysa v1 displaystyle v 1 ve v2 displaystyle v 2 yukarida da gordugumuz uzere u1 displaystyle u 1 v1 displaystyle v 1 degeri kucuktur daha hafif olan cisime vurmak hizi cok degistirmez ama daha agir olan cisime vuruldugunda yuksek hizda sicrama yapan hizlanan cisime neden olur Farkli kutlelerde olan cisimlerin esnek carpismalari Bir notron moderatoru asagi hizli notronlari yavaslatan bir ortam boylece bir zincirleme reaksiyon surdurme yetenegine sahip termal notronlar donusturerek kolayca notron absorbe olmayan ek ozelligi ile Isik cekirdekleri ile atomlarin bir malzeme dolu olmasinin nedeni budur hafif cekirdeklerde notron ayni kutleye hakkinda sahip Bir boyutta relativistik esnek carpisma Ozel relativiteye gore p mv1 v2c2 displaystyle p frac mv sqrt 1 frac v 2 c 2 p herhangi bir m kutleli v hizli parcacigin momentumudur c ise isik hizidir Momentum cercevesindeki merkezde toplam momentum sifira esit olur p1 p2 displaystyle p 1 p 2 p12 p22 displaystyle p 1 2 p 2 2 m12c4 p12c2 m22c4 p22c2 E displaystyle sqrt m 1 2 c 4 p 1 2 c 2 sqrt m 2 2 c 4 p 2 2 c 2 E p1 E4 2E2m12c4 2E2m22c4 m14c8 2m12m22c8 m24c8cE displaystyle p 1 pm frac sqrt E 4 2E 2 m 1 2 c 4 2E 2 m 2 2 c 4 m 1 4 c 8 2m 1 2 m 2 2 c 8 m 2 4 c 8 cE u1 v1 displaystyle u 1 v 1 m1 displaystyle m 1 ilk carpisan cismin kutlesine karsilik gelir m2 displaystyle m 2 ikinci carpisan cismin kutlesine karsilik gelir u1 displaystyle u 1 ilk carpisan cismin ilk hizidir u2 displaystyle u 2 ikinci carpisan cismin ilk hizidir v1 displaystyle v 1 carpismadan sonra ilk carpisan cismin hizidir v2 displaystyle v 2 carpismadan sonra ikinci carpisan cismin hizidir p1 displaystyle p 1 ilk carpisan cismin momentumudur p2 displaystyle p 2 ikinci carpisan cismin momentumudur ve c displaystyle c isik hizi E displaystyle E ve sistemin toplam enerjisini belirtir ornegin carpisan cisimlerin kinetik enerjilerinin toplami ve kutlelerinin toplami Sistemin toplam enerjisi ve toplam momentumu korunur ve carpisan cisimlerin geri kalan kutleleri degismez carpisan cisimlerin momentumlari carpisan cisimlerin kutleleriyle toplam enerji ve toplam momentumlariyla dogru orantilidir Carpisan cismin momentumunun buyuklugu carpismadan sonra degismez ancak hareketinin yonu momentum merkezine gore ters yondedir Klasik fizikteki cok parcacikli ve yuksek boyutlu sistemler klasik atomlarin bir araya gelmesiyle olusacaklardir Ornegin hava masasi deneylerinde kullanilan diskler uc boyutlu cisimler olmalarina ragmen iki boyuta kisitlanmis hareketlerinin incelenmesi soz konusu oldugundan iki boyutlu olarak ele alinabilmektedirler Eger deneyler yapilirken disklerin kendi simetri eksenleri etrafindaki olasi donmeler spin hareketleri engellenebilirse o zaman disklerin hareketleri sadece kutle merkezlerinin hareketleri ile karakterize edilebileceginden diskler noktasal parcaciklar olarak dusunulebilirler Bu donmelerin kaynaklari elektromagnetik kokenli olan surtunme kuvvetlerinin olusturdugu torklardir Hava masasinin ozelligi katilarin birbirlerine temas ederek hareket etmeleri sirasinda var olan siddetli kinetik surtunme kuvvetlerini bunlarin yaninda ihmal edilebilecek buyukluklere sahip hava surtunmelerine indirgiyor olmasidir Ancak ihmal edilmelerine ragmen var olan bu surtunme kuvvetlerinden kaynaklanabilecek donmelerin olusmalari durumunda deneysel hatalar artacaktir Donmelerin soz konusu oldugu kapali varsayilabilecek esnek bir carpismada kinetik enerji korunacaktir ancak artik kinetik enerjinin hem oteleme hem de donmeden kaynaklanan kisimlari olacaktir Klasik noktasal parcaciklar da carpisirlarken birbirlerine temas etmeyebilirler ornek olarak biri durgun digeri de onunla etkilesecek sekilde hareket eden ayni elektrik yukune sahip noktasal parcaciklarin esnek sacilmalari incelenebilir Boyle bir elektriksel sisteme esdeger mekaniksel bir sistem sadece temas etmek suretiyle etkilestikleri varsayilan iki disk ve onlarin otelemesel esnek carpismalari ile verilebilir Klasik Mekanik sadece iyi bir yaklasimdir Klasik Mekanik makroskopik boyuttaki cisimlerle ve isik hizindan daha yavas olan hizlarla ugrastiginda bize daha kesin sonuclar verir Klasik limitin otesindeyse sonuclar yanlis olur Momentum merkezinde ve klasik mekanige gore Esnek carpisma yapan iki cisimli sistemin toplam momentumu momentum referans cercevesine baglidir m1u1 m2u2 m1v1 m2v2 0 displaystyle m 1 u 1 m 2 u 2 m 1 v 1 m 2 v 2 0 m1u12 m2u22 m1v12 m2v22 displaystyle m 1 u 1 2 m 2 u 2 2 m 1 v 1 2 m 2 v 2 2 m2u2 22m1 m2u2 22m2 m2v2 22m1 m2v2 22m2 displaystyle frac m 2 u 2 2 2m 1 frac m 2 u 2 2 2m 2 frac m 2 v 2 2 2m 1 frac m 2 v 2 2 2m 2 m1 m2 m2u2 2 m1 m2 m2v2 2 displaystyle m 1 m 2 m 2 u 2 2 m 1 m 2 m 2 v 2 2 u2 v2 displaystyle u 2 v 2 m1u1 22m1 m1u1 22m2 m1v1 22m1 m1v1 22m2 displaystyle frac m 1 u 1 2 2m 1 frac m 1 u 1 2 2m 2 frac m 1 v 1 2 2m 1 frac m 1 v 1 2 2m 2 m1 m2 m1u1 2 m1 m2 m1v1 2 displaystyle m 1 m 2 m 1 u 1 2 m 1 m 2 m 1 v 1 2 u1 v1 displaystyle u 1 v 1 u1 v1 displaystyle u 1 v 1 Diger farkliliklara ragmen goreli hesaplamada dogru kalir Ozel Gorelilik icinde onermelerden biri Fizik Kanunlarinin tum atalet cerceveleri referansinda degismez olmasi gerektigini belirtiyor Yani toplam momentum belirli referans cercevesinde korunursa toplam momentumun miktari cerceveye bagli olmasina ragmen toplam momentum herhangi bir referans cercevesinde de korunur Bu yuzden bir cerceveden diger referans cercevesine ya da digerine donusturulerek istenilen sonuclari almak mumkundur Belli bir referans cercevesinde toplam momentum herhangi bir yerde olabilir m1u11 u12 c2 m2u21 u22 c2 m1v11 v12 c2 m2v21 v22 c2 pT displaystyle frac m 1 u 1 sqrt 1 u 1 2 c 2 frac m 2 u 2 sqrt 1 u 2 2 c 2 frac m 1 v 1 sqrt 1 v 1 2 c 2 frac m 2 v 2 sqrt 1 v 2 2 c 2 p T m1c21 u12 c2 m2c21 u22 c2 m1c21 v12 c2 m2c21 v22 c2 E displaystyle frac m 1 c 2 sqrt 1 u 1 2 c 2 frac m 2 c 2 sqrt 1 u 2 2 c 2 frac m 1 c 2 sqrt 1 v 1 2 c 2 frac m 2 c 2 sqrt 1 v 2 2 c 2 E Ikili sekilde hareket eden cisimlerin toplam momentumlarina baktigimizda pT displaystyle p T toplam enerji E displaystyle E ve hizi vc displaystyle v c kutle merkezindeki hizi Kutle merkezine bagli olarak toplam momentum sifira esittir Ve su sekilde gosterilebilir vc displaystyle v c vc pTc2E displaystyle v c frac p T c 2 E Ve simdi de momentum merkezindeki carpismadan onceki hizlarina bakacak olursak eger u1 displaystyle u 1 ve u2 displaystyle u 2 u1 u1 vc1 u1vcc2 displaystyle u 1 frac u 1 v c 1 frac u 1 v c c 2 u2 u2 vc1 u2vcc2 displaystyle u 2 frac u 2 v c 1 frac u 2 v c c 2 v1 u1 displaystyle v 1 u 1 v2 u2 displaystyle v 2 u 2 v1 v1 vc1 v1 vcc2 displaystyle v 1 frac v 1 v c 1 frac v 1 v c c 2 v2 v2 vc1 v2 vcc2 displaystyle v 2 frac v 2 v c 1 frac v 2 v c c 2 u1 c displaystyle u 1 ll c and u2 c displaystyle u 2 ll c pT displaystyle p T m1u1 m2u2 displaystyle m 1 u 1 m 2 u 2 vc displaystyle v c m1u1 m2u2m1 m2 displaystyle frac m 1 u 1 m 2 u 2 m 1 m 2 u1 displaystyle u 1 u1 vc displaystyle u 1 v c m1u1 m2u1 m1u1 m2u2m1 m2 m2 u1 u2 m1 m2 displaystyle frac m 1 u 1 m 2 u 1 m 1 u 1 m 2 u 2 m 1 m 2 frac m 2 u 1 u 2 m 1 m 2 u2 displaystyle u 2 m1 u2 u1 m1 m2 displaystyle frac m 1 u 2 u 1 m 1 m 2 v1 displaystyle v 1 m2 u2 u1 m1 m2 displaystyle frac m 2 u 2 u 1 m 1 m 2 v2 displaystyle v 2 m1 u1 u2 m1 m2 displaystyle frac m 1 u 1 u 2 m 1 m 2 v1 displaystyle v 1 v1 vc displaystyle v 1 v c m2u2 m2u1 m1u1 m2u2m1 m2 u1 m1 m2 2m2u2m1 m2 displaystyle frac m 2 u 2 m 2 u 1 m 1 u 1 m 2 u 2 m 1 m 2 frac u 1 m 1 m 2 2m 2 u 2 m 1 m 2 v2 displaystyle v 2 u2 m2 m1 2m1u1m1 m2 displaystyle frac u 2 m 2 m 1 2m 1 u 1 m 1 m 2 Bu yuzden carpisan iki cismin hizi da isik hizindan yani yaklasik olarak 300 milyon m s cok cok cok dusuk oldugunda klasik hesaplama yontemi icin bu sonuclar dogrudur Carpisma icin baska relativistik turetilmis formuller Hizin parametresi olarak adlandirilan parametreden soz etmistik s displaystyle s v c tanh s es e ses e s displaystyle v c mbox tanh s frac e s e s e s e s bundan dolayi su formulu elde ederiz es c vc v displaystyle e s sqrt frac c v c v Relativistik enerji ve momentum su sekilde aciklanabilir E mc21 v2c2 mc2cosh s displaystyle E frac mc 2 sqrt 1 frac v 2 c 2 mc 2 mbox cosh s p mv1 v2c2 mc sinh s displaystyle p frac mv sqrt 1 frac v 2 c 2 mc mbox sinh s Carpisan kutlelerin enerji toplamlari icin denklemler ve carpisan kutlelerin momentum toplamlari icin denklemler ise soyle m1 displaystyle m 1 ve m2 displaystyle m 2 velocitiesv1 displaystyle v 1 v2 displaystyle v 2 u1 displaystyle u 1 u2 displaystyle u 2 hiz parametresine bagli olarak s1 displaystyle s 1 s2 displaystyle s 2 s3 displaystyle s 3 s4 displaystyle s 4 yeterli guce bolunmesinden sonra c displaystyle c su formuller elde edilecektir m1cosh s1 m2cosh s2 m1cosh s3 m2cosh s4 displaystyle m 1 mbox cosh s 1 m 2 mbox cosh s 2 m 1 mbox cosh s 3 m 2 mbox cosh s 4 m1sinh s1 m2sinh s2 m1sinh s3 m2sinh s4 displaystyle m 1 mbox sinh s 1 m 2 mbox sinh s 2 m 1 mbox sinh s 3 m 2 mbox sinh s 4 ve birbirine bagli denklemler yukaridaki denklemin toplami m1es1 m2es2 m1es3 m2es4 displaystyle m 1 e s 1 m 2 e s 2 m 1 e s 3 m 2 e s 4 denklemin her iki tarafinin karesinden de enerjiden momentum cikarilir ve su tanim kullanilir cosh2 s sinh2 s 1 displaystyle mbox cosh 2 s mbox sinh 2 s 1 ve denklemleri basitlestirdikten sonra su formulleri elde ederiz 2m1m2 cosh s1 sinh s2 cosh s2 sinh s1 2m1m2 cosh s3 sinh s4 cosh s4 sinh s3 displaystyle 2m 1 m 2 mbox cosh s 1 mbox sinh s 2 mbox cosh s 2 mbox sinh s 1 2m 1 m 2 mbox cosh s 3 mbox sinh s 4 mbox cosh s 4 mbox sinh s 3 kutlesi sifir olmayan cisimler icin su formulleri elde ederiz cosh s1 s2 cosh s3 s4 displaystyle mbox cosh s 1 s 2 mbox cosh s 3 s 4 cosh s displaystyle mbox cosh s fonksiyonu cifttir ve bu denklem icin iki tane cozum elde ederiz s1 s2 s3 s4 displaystyle s 1 s 2 s 3 s 4 s1 s2 s3 s4 displaystyle s 1 s 2 s 3 s 4 son denklemden bir degere sahip cozum elde ederiz ve sunu cozeriz s2 displaystyle s 2 ve bagimli denklemin yerine gecer ve sunu elde ederiz es1 displaystyle e s 1 ve daha sonra da es2 displaystyle e s 2 bu gelir es1 es4m1es3 m2es4m1es4 m2es3 displaystyle e s 1 e s 4 frac m 1 e s 3 m 2 e s 4 m 1 e s 4 m 2 e s 3 es2 es3m1es3 m2es4m1es4 m2es3 displaystyle e s 2 e s 3 frac m 1 e s 3 m 2 e s 4 m 1 e s 4 m 2 e s 3 Problemin cozumu bu sekilde ama hiz parametreleriyle aciklanir Hiz parametreleri icin yer degistirme formulleri uygulandiginda v1 c tanh s1 es1 e s1es1 e s1 displaystyle v 1 c mbox tanh s 1 frac e s 1 e s 1 e s 1 e s 1 v2 c tanh s2 es2 e s2es2 e s2 displaystyle v 2 c mbox tanh s 2 frac e s 2 e s 2 e s 2 e s 2 Bir onceki adim uygulandiginda da bu formul elde edilir es3 c u1c u1 displaystyle e s 3 sqrt frac c u 1 c u 1 ve es4 c u2c u2 displaystyle e s 4 sqrt frac c u 2 c u 2 uzunca bir donusum formulu uyguladiktan sonra yerine koyulan ile birlikte Z 1 u12 c2 1 u22 c2 displaystyle Z sqrt 1 u 1 2 c 2 1 u 2 2 c 2 Bu sonucu elde ederiz v1 2m1m2c2u2Z 2m22c2u2 m12 m22 u1u22 m12 m22 c2u12m1m2c2Z 2m22u1u2 m12 m22 u22 m12 m22 c2 displaystyle v 1 frac 2m 1 m 2 c 2 u 2 Z 2m 2 2 c 2 u 2 m 1 2 m 2 2 u 1 u 2 2 m 1 2 m 2 2 c 2 u 1 2m 1 m 2 c 2 Z 2m 2 2 u 1 u 2 m 1 2 m 2 2 u 2 2 m 1 2 m 2 2 c 2 v2 2m1m2c2u1Z 2m12c2u1 m12 m22 u12u2 m22 m12 c2u22m1m2c2Z 2m12u1u2 m22 m12 u12 m12 m22 c2 displaystyle v 2 frac 2m 1 m 2 c 2 u 1 Z 2m 1 2 c 2 u 1 m 1 2 m 2 2 u 1 2 u 2 m 2 2 m 1 2 c 2 u 2 2m 1 m 2 c 2 Z 2m 1 2 u 1 u 2 m 2 2 m 1 2 u 1 2 m 1 2 m 2 2 c 2 Iki boyutta esnek carpismaBir boyutlu esnek carpismalarin disindaki esnek carpismalarda sadece momentumun ve kinetik enerjinin korunumu carpisma sonrasi hizlari belirlemeye yetmeyecektir Mesela iki boyutlu esnek carpisma durumunda iki parcacik icin carpisma sonrasi iki hiz ve her hizin iki bileseni oldugundan dort tane bilinmeyen vardir Bu dort bilinmeyen momentumun korunumu nedeniyle iki ve kinetik enerjinin korunumu nedeniyle de bir toplam uc tane skaler denklem ile kisitlanirlar ancak son hizlarin bulunmasi icin fazladan bir bilgiye ihtiyac duyulmaktadir Bu bilgiye deney ile ulasilabilir ve cogu zaman carpisma sonrasi parcaciklardan birinin ilerleme yonunun probleme adapte edilmis eksenlerden biriyle yaptigi aci sacilma acisi bu bilgi icin kullanilir Iki boyutta iki carpisan cisimlerin her durumunda her cismin hizi icin iki dikey hiz bolunmesi gerekir Bir teget carpisan cisimlerin sik gorulen normal yuzeylerine temas noktasinda digeri de bir carpisma hatti boyunca Carpisma sadece carpma hatti boyunca kuvvet olusturdugu icin carpisma noktasina teget olan hizlari degismez Carpisma hatti boyunca hizlar da tek boyutlu bir carpisma ile ayni denklemler de kullanilabilir Son hizlar daha sonra iki yeni bilesen hizlari hesaplanabilir ve carpisma noktasina baglidir Iki boyutta esnek carpisma Herhangi bir zamanda momentum cercevesinin merkezinde iki organlarinin hizlari kitlelere ters orantili buyukluklerde ters yonlerde bulunmaktadir Esnek carpismada bu buyuklukleri degismez Uzaklik cisimlerin sekil ve carpma noktasina bagli olarak degisebilir Ornegin kureler halinde acisi iki govde merkezlerinin paralel yollari arasindaki uzakliga baglidir Yonu sifir olmayan herhangi bir degisiklik mumkundur Bu mesafe hizlari carpisma tersine sifir ise kurelerin yaricaplari toplami yakin ise iki cisim sadece biraz saptirilir Ikinci parcacigin carpismadan once hareketsiz oldugunu varsayarsak iki parcacigin sapma acisi ϑ1 displaystyle vartheta 1 and ϑ2 displaystyle vartheta 2 sapma acisiyla ilgili olarak 8 displaystyle theta sistemde kutle merkezi by tan ϑ1 m2sin 8m1 m2cos 8 ϑ2 p 82 displaystyle tan vartheta 1 frac m 2 sin theta m 1 m 2 cos theta qquad vartheta 2 frac pi theta 2 Carpismadan sonraki parcaciklarin hizlarinin buyuklukleri v1 v1m12 m22 2m1m2cos 8m1 m2 v2 v12m1m1 m2sin 82 displaystyle v 1 v 1 frac sqrt m 1 2 m 2 2 2m 1 m 2 cos theta m 1 m 2 qquad v 2 v 1 frac 2m 1 m 1 m 2 sin frac theta 2 Iki boyutta iki cisimli carpisma Ilk topun x ve y son hiz bilesenleri su sekilde hesaplanabilir v1x v1cos 81 f m1 m2 2m2v2cos 82 f m1 m2cos f v1sin 81 f cos f p2 v1y v1cos 81 f m1 m2 2m2v2cos 82 f m1 m2sin f v1sin 81 f sin f p2 displaystyle begin aligned v 1x amp frac v 1 cos theta 1 varphi m 1 m 2 2m 2 v 2 cos theta 2 varphi m 1 m 2 cos varphi 0 2em amp quad v 1 sin theta 1 varphi cos varphi frac pi 2 0 8em v 1y amp frac v 1 cos theta 1 varphi m 1 m 2 2m 2 v 2 cos theta 2 varphi m 1 m 2 sin varphi 0 2em amp quad v 1 sin theta 1 varphi sin varphi frac pi 2 end aligned v1 and v2 cisimlerin orijinal hizlarinin skalar boyutlari m1 and m2 are their masses 81 and 82 ve hareket acilari yani v1x v1cos 81 v1y v1sin 81 displaystyle v 1x v 1 cos theta 1 v 1y v 1 sin theta 1 asagidan saga dogru hareket eden bir aci ya 45 ya da 315 acidir ve kucuk phi f baglanti acisidir Ikinci topun x ve y hizlarini elde etmek icin 1 ve 2 diye adlandirabiliriz Bu denklem iki cisim arasindaki etkilesimi kolayca temas acisi paralel olacak sekilde x ve y ekseni ile tek boyutlu olarak hesaplanabilir ve ayrica nesnelerin hizlarini da kolay bir sekilde hesaplamaya yarar yani temas acisi boyunca hesaplanan turetilmis bir buyukluktur ve nesneler daha sonra gercek x ve y bilesenlerini hizlarini almak icin geri ozgun yonune dondurulur Bir serbest aci gosteriminde degisen hizlar merkez kullanilarak hesaplanir x1 ve x2 v1 v1 2m2m1 m2 v1 v2 x1 x2 x1 x2 2 x1 x2 v2 v2 2m1m1 m2 v2 v1 x2 x1 x2 x1 2 x2 x1 displaystyle begin aligned mathbf v 1 amp mathbf v 1 frac 2m 2 m 1 m 2 frac langle mathbf v 1 mathbf v 2 mathbf x 1 mathbf x 2 rangle mathbf x 1 mathbf x 2 2 mathbf x 1 mathbf x 2 mathbf v 2 amp mathbf v 2 frac 2m 1 m 1 m 2 frac langle mathbf v 2 mathbf v 1 mathbf x 2 mathbf x 1 rangle mathbf x 2 mathbf x 1 2 mathbf x 2 mathbf x 1 end aligned acili ayraclar iki vektorun ic carpimini ve skaler carpimini gosterirler Ayrica bakinizCarpismalar Esnek olmayan carpismalarKaynakca Landau Lifshitz E M 1976 Mechanics 3 3ad1 L D bas Pergamon Press s 46 ISBN 0 08 021022 8 Craver William E Elastic Collisions Williamecraver wix com Wix com 13 Aug 2013 Web 13 Aug 2013 lt http williamecraver wix com elastic equations 24 Aralik 2015 tarihinde Wayback Machine sitesinde gt Raymond David J 10 4 1 Elastic collisions A radically modern approach to introductory physics Volume 1 Fundamental principles Socorro NM New Mexico Tech Press ISBN 978 0 9830394 5 7 Dis baglantilarRigid Body Collision Resolution in three dimensions 6 Ocak 2016 tarihinde Wayback Machine sitesinde including a derivation using the conservation laws VNE Rigid Body Collision Simulation27 Ekim 2010 tarihinde Wayback Machine sitesinde Small Open Source 3D engine with easy to understand implementation of elastic collisions in C Visualize 2 D Collision 24 Aralik 2015 tarihinde Wayback Machine sitesinde Free simulation of 2 particle collision with user adjustable coefficient of restitution and particle velocities Requires Adobe Shockwave 2 Dimensional Elastic Collisions without Trigonometry 25 Aralik 2015 tarihinde Wayback Machine sitesinde Explanation of how to calculate 2 dimensional elastic collisions using vectors Bouncescope 20 Subat 2016 tarihinde Wayback Machine sitesinde Free simulator of elastic collisions of dozens of user configurable objects Managing ball vs ball collision with Flash 24 Aralik 2015 tarihinde Wayback Machine sitesinde Flash script to manage elastic collisions among any number of spheres Elastic collision derivation 14 Subat 2017 tarihinde Wayback Machine sitesinde Elastic collision formula derivation if one of balls velocity is 0 19 Ocak 2016 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans








































































