Parçacık fiziğinde elektrozayıf etkileşim, doğanın bilinen iki veya dört temel etkileşiminin birleşimin bir tanımıdır: elektromanyetizm ve zayıf etkileşim. Her gün düşük enerjilerde, bu iki kuvvet çok farklı oluşsa da, teori modelleri aynı kuvvetin iki farklı etkisi gibidir. Yukarıdaki birleştirme enerjisi, yaklaşık 100 GeV, tek bir elektrozayıf kuvvet oluşturabilir. Bu yüzden, eğer evren yeterince sıcaksa (Big Bang’den kısa bir sonra olan bir sıcaklık ortalama 1015 K), elektromanyetik kuvvet ve zayıf kuvvet birleşmiş bir elektrozayıf kuvvete dönüşür. Elektrozayıf dönem boyunca, zayıf kuvvet güçlü kuvvetten ayrılır. Kuark dönem boyunca, elektrozayıf kuvvet elektromanyetik ve zayıf kuvvetten ayrılır.
Sheldon Glashow, Abdus Salam ve Steven Weinberg, temel parçacıklar arasındaki zayıf ve elektromanyetik etkileşimin birleşimine katkılarından ötürü 1979’da Nobel Fizik ödülünü aldılar. Elektrozayıf etkileşimlerin varlığı deneysel olarak iki adımda sabitlendi, ilki 1973’te Gargamelle işbirliği ile nötrino saçılmasındaki nötr akımların keşfiydi. Ikincisi ise dönüşmüş Super Proton Synchroton’undaki proton/antiproton çarpışmalarının W ve Z ölçü bozonlarının keşfini içeren 1983’teki UA1 ve UA2 işbirliğidir. 1999 yılında Gerardus 't Hooft ve Martinus Veltman elektrozayıf teorinin yeniden normalleştirilebildiğini gösterdiği için Nobel ödülü aldı.
Gelişimi
Uzun zamandır, zayıf kuvvetin elektromanyetik kuvvetle yakın bir ilişisinin bulunduğu düşünülüyordu. Nihayet, 10−18 m gibi küçük mesafelerde zayıf etkileşimin gücünün, elektromanyetik etkileşiminkiyle kıyaslanabilir olduğu belirlendi. Öte yandan, bunun 30 misli, yani 3x10−17 m mesafe düzeyinde, zayıf etkileşimin gücü, elektromanyetik etkileşiminkinin 1/10,000'ine iniyordu. Bir nötron veya protonu oluşturan kuarkların arasındaki tipik mesafelerde (10−15 m) ise, bu oran çok daha küçülüyordu. Sonuç olarak, zayıf ve elektromanyetik kuvvetlerin gücünün, esas olarak eşit düzeyde olduğu sonucuna varıldı. Çünkü bir etkileşimin gücü, taşıyıcı parçacığın kütlesine ve etkileşim mesafesine, güçlü bir şekilde bağlıydı. İki kuvvetin güç düzeyleri arasındaki gözlemlenen fark, görece çok ağır olan W ve Z parçacıkları ile, bilindiği kadarıyla kütlesi olmayan foton arasındaki kütle farkından kaynaklanıyordu.
Sonuç olarak Standart Model'de elektromanyetik ve zayıf etkileşim; Glashow, Salam ve Weinberg tarafından geliştirilmiş olan birleşik bir 'elektrozayıf' kuramda birleştirilmiş bulunuyor. Bu iki alanın 'Birleşik Alanlar Kuramı;' o zamana kadar zayıf etkileşimin tek taşıyıcısı olduğu düşünülen W parçacıklarının kütlesini hesaplayabildiği gibi, yeni bir tür zayıf etkileşimin ve bu etkileşimin taşıyıcısı olan Z parçacığının varlığını da öngördü.
Bu kuvvetlerin birleştirilmesi ve tek bir teoriyle açıklanması bu kişilere 1979 Nobel ödülünü kazandırmıştır. Bu teorinin kurulması, fizikçilerin yıllardır kurmaya çalıştıkları büyük birleşik teoriye giden yolda atılan ilk başarılı adımdır. Daha önce Albert Einstein, kütleçekim ile elektromanyetik kuvveti birleştirmeye çalışmış ancak başarısız olmuştu.
Formülasyon
Bilinen bazı temel parçacıklar; zayıf eşspin modeli T3, zayıf aşırıyük YW, zayıf birleşme açısı boyunca Q elektrik yükünü gösteriyor. Nötr Higgs alanı (çevrelenmiş) elektrozayıf simetriyi bozar ve kütlesini diğer parçacıklara vermek için onlarla etkileşime geçer. Higgs alanının üç bileşeni çok büyük W ve Z bozonlarının bir parçası olmaya başlar.
Matematiksel olarak, birleşime bir SU(2) × U(1) ölçüm grubu altında ulaşılır. Ilgili ayar bozonları SU(2) (W1, W2, and W3)’dan zayıf eşspinli üç W, U(1)’den zayıf aşırıyüklü B bozonudur ve hepsi kütlesizdir.
Standart modelde W, Z bozonları ve foton; Higgs mekanizmasının neden olduğu SU(2) × U(1)Y to U(1)em’dan elektrozayıf simetrinin ani simetri bozulması ile üretilir. U(1)Y and U(1)em, U(1)’in farklı kopyalarıdır ve üretici U(1)em,Q = Y/2 + I3 olarak verilir; Y U(1)Y’in üreticisidir; I3 ise SU(2)’nin üreticilerinden (zayıf eşspinin bir bileşeni) biridir.
Ani simetri bozulması W3 ve B bozonlarının iki farklı bozon gibi davranmasına yol açar - Z0 ve (γ) aşağıdaki gibidir:

θW zayıf birleşme açısıdır. Parçacıkları gösteren eksenler (W3, B) düzlemi boyunca θW açısı ile dönmüştür. Bu durum Z0 kütlesi ve W± arasında bir çelişki yaratır (sırasıyla MZ ve MW)
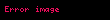
W1 ve W2 bozonları daha büyük yüklü bozonlar oluşturmak için birleşir:
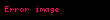
Elektromanyetizm ve zayıf kuvvet arasında fark oluşur, çünkü Higgs bozonu için Y ve I3‘ün doğrusal birleşimi vardır. U(1)em bu doğrusal birleşme tarafından üretilen grup olarak tanımlanır ve Higgs ile etkileşmediğinden bozulmaz.
Lagrangian
Elektrozayıf simetrinin bozulmasından önce
Elektrozayıf etkileşimleri Lagrangian, elektrozayıf simetriden önce dört gruba ayırdı
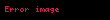
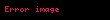



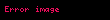
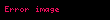




h Higgs alanını F tanımlar.
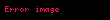
y terimi Higgs beklenen bir vakum değerini elde ettikten sonra fermion kütlelerini oluşturan Yukawa etkileşimini verir.
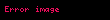
Elektrozayıf simetrinin bozulmasından sonra
Higgs beklenen bir vakum değerini elde ettikten sonra Lagrangian bunu tekrar tanımlar. Karmaşıklığından ötürü, Lagrangian aşağıdaki denkliği birçok parçaya ayırarak tanımlamıştır.

Kinetik terim 

toplam fermion teorisine geçer (quarklar ve leptonlar), alanlar 
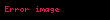
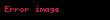


(ilgili alanı X ile yer değiştirin ve ayar grubu için yapı sabitleri fabc).
Lagrangian’ın bileşenleri nötr akım ve yüklü akım fermionlar ve ayar bozonları arasında bir etkileşim içerir.

Elektromanyetik akım 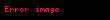
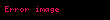
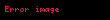
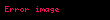


Lagrangian’ın yüklü akım kısmı şöyledir:


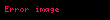


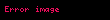

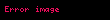
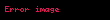


Zayıf eşleşmelerde 
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Parcacik fiziginde elektrozayif etkilesim doganin bilinen iki veya dort temel etkilesiminin birlesimin bir tanimidir elektromanyetizm ve zayif etkilesim Her gun dusuk enerjilerde bu iki kuvvet cok farkli olussa da teori modelleri ayni kuvvetin iki farkli etkisi gibidir Yukaridaki birlestirme enerjisi yaklasik 100 GeV tek bir elektrozayif kuvvet olusturabilir Bu yuzden eger evren yeterince sicaksa Big Bang den kisa bir sonra olan bir sicaklik ortalama 1015 K elektromanyetik kuvvet ve zayif kuvvet birlesmis bir elektrozayif kuvvete donusur Elektrozayif donem boyunca zayif kuvvet guclu kuvvetten ayrilir Kuark donem boyunca elektrozayif kuvvet elektromanyetik ve zayif kuvvetten ayrilir Sheldon Glashow Abdus Salam ve Steven Weinberg temel parcaciklar arasindaki zayif ve elektromanyetik etkilesimin birlesimine katkilarindan oturu 1979 da Nobel Fizik odulunu aldilar Elektrozayif etkilesimlerin varligi deneysel olarak iki adimda sabitlendi ilki 1973 te Gargamelle isbirligi ile notrino sacilmasindaki notr akimlarin kesfiydi Ikincisi ise donusmus Super Proton Synchroton undaki proton antiproton carpismalarinin W ve Z olcu bozonlarinin kesfini iceren 1983 teki UA1 ve UA2 isbirligidir 1999 yilinda Gerardus t Hooft ve Martinus Veltman elektrozayif teorinin yeniden normallestirilebildigini gosterdigi icin Nobel odulu aldi GelisimiUzun zamandir zayif kuvvetin elektromanyetik kuvvetle yakin bir ilisisinin bulundugu dusunuluyordu Nihayet 10 18 m gibi kucuk mesafelerde zayif etkilesimin gucunun elektromanyetik etkilesiminkiyle kiyaslanabilir oldugu belirlendi Ote yandan bunun 30 misli yani 3x10 17 m mesafe duzeyinde zayif etkilesimin gucu elektromanyetik etkilesiminkinin 1 10 000 ine iniyordu Bir notron veya protonu olusturan kuarklarin arasindaki tipik mesafelerde 10 15 m ise bu oran cok daha kuculuyordu Sonuc olarak zayif ve elektromanyetik kuvvetlerin gucunun esas olarak esit duzeyde oldugu sonucuna varildi Cunku bir etkilesimin gucu tasiyici parcacigin kutlesine ve etkilesim mesafesine guclu bir sekilde bagliydi Iki kuvvetin guc duzeyleri arasindaki gozlemlenen fark gorece cok agir olan W ve Z parcaciklari ile bilindigi kadariyla kutlesi olmayan foton arasindaki kutle farkindan kaynaklaniyordu Sonuc olarak Standart Model de elektromanyetik ve zayif etkilesim Glashow Salam ve Weinberg tarafindan gelistirilmis olan birlesik bir elektrozayif kuramda birlestirilmis bulunuyor Bu iki alanin Birlesik Alanlar Kurami o zamana kadar zayif etkilesimin tek tasiyicisi oldugu dusunulen W parcaciklarinin kutlesini hesaplayabildigi gibi yeni bir tur zayif etkilesimin ve bu etkilesimin tasiyicisi olan Z parcaciginin varligini da ongordu Bu kuvvetlerin birlestirilmesi ve tek bir teoriyle aciklanmasi bu kisilere 1979 Nobel odulunu kazandirmistir Bu teorinin kurulmasi fizikcilerin yillardir kurmaya calistiklari buyuk birlesik teoriye giden yolda atilan ilk basarili adimdir Daha once Albert Einstein kutlecekim ile elektromanyetik kuvveti birlestirmeye calismis ancak basarisiz olmustu FormulasyonBilinen bazi temel parcaciklar zayif esspin modeli T3 zayif asiriyuk YW zayif birlesme acisi boyunca Q elektrik yukunu gosteriyor Notr Higgs alani cevrelenmis elektrozayif simetriyi bozar ve kutlesini diger parcaciklara vermek icin onlarla etkilesime gecer Higgs alaninin uc bileseni cok buyuk W ve Z bozonlarinin bir parcasi olmaya baslar Matematiksel olarak birlesime bir SU 2 U 1 olcum grubu altinda ulasilir Ilgili ayar bozonlari SU 2 W1 W2 and W3 dan zayif esspinli uc W U 1 den zayif asiriyuklu B bozonudur ve hepsi kutlesizdir Standart modelde W Z bozonlari ve foton Higgs mekanizmasinin neden oldugu SU 2 U 1 Y to U 1 em dan elektrozayif simetrinin ani simetri bozulmasi ile uretilir U 1 Y and U 1 em U 1 in farkli kopyalaridir ve uretici U 1 em Q Y 2 I3 olarak verilir Y U 1 Y in ureticisidir I3 ise SU 2 nin ureticilerinden zayif esspinin bir bileseni biridir Ani simetri bozulmasi W3 ve B bozonlarinin iki farkli bozon gibi davranmasina yol acar Z0 ve g asagidaki gibidir gZ0 cos 8Wsin 8W sin 8Wcos 8W BW3 displaystyle begin pmatrix gamma Z 0 end pmatrix begin pmatrix cos theta W amp sin theta W sin theta W amp cos theta W end pmatrix begin pmatrix B W 3 end pmatrix 8W zayif birlesme acisidir Parcaciklari gosteren eksenler W3 B duzlemi boyunca 8W acisi ile donmustur Bu durum Z0 kutlesi ve W arasinda bir celiski yaratir sirasiyla MZ ve MW MZ MWcos 8W displaystyle M Z frac M W cos theta W W1 ve W2 bozonlari daha buyuk yuklu bozonlar olusturmak icin birlesir W 12 W1 iW2 displaystyle W pm frac 1 sqrt 2 W 1 mp iW 2 Elektromanyetizm ve zayif kuvvet arasinda fark olusur cunku Higgs bozonu icin Y ve I3 un dogrusal birlesimi vardir U 1 em bu dogrusal birlesme tarafindan uretilen grup olarak tanimlanir ve Higgs ile etkilesmediginden bozulmaz LagrangianElektrozayif simetrinin bozulmasindan once Elektrozayif etkilesimleri Lagrangian elektrozayif simetriden once dort gruba ayirdi LEW Lg Lf Lh Ly displaystyle mathcal L EW mathcal L g mathcal L f mathcal L h mathcal L y Lg displaystyle mathcal L g terimi uc tane W parcaciklari ve B parcasi arasinda etkilesimi tanimlar Lg 14WamnWmna 14BmnBmn displaystyle mathcal L g frac 1 4 W a mu nu W mu nu a frac 1 4 B mu nu B mu nu Wamn displaystyle W a mu nu a 1 2 3 displaystyle a 1 2 3 ve Bmn displaystyle B mu nu zayif esspinler ve zayif asiriyuklu alanlar icin alan guclendirici tensorlerdir Lf displaystyle mathcal L f standard Model fermionlarinin kinetik bir terimidir Ayar bozonlari ve fermionlar arasindaki etkilesim olcu aleti esdegisken turev boyuncadir Lf Q iiD Qi u iiD ui d iiD di L iiD Li e iiD ei displaystyle mathcal L f overline Q i iD Q i overline u i iD u i overline d i iD d i overline L i iD L i overline e i iD e i i displaystyle i uc nesil fermionu gecer Q displaystyle Q u displaystyle u ve d displaystyle d sol el ciftleri sag el teklileri ve sag el tekli kuark alan asagisidir ve sol el ciftleri ve sag el tekli elektron alanlaridir h Higgs alanini F tanimlar Lh Dmh 2 l h 2 v22 2 displaystyle mathcal L h D mu h 2 lambda left h 2 frac v 2 2 right 2 y terimi Higgs beklenen bir vakum degerini elde ettikten sonra fermion kutlelerini olusturan Yukawa etkilesimini verir Ly yuijϵabhb Q iaujc ydijhQ idjc yeijhL iejc h c displaystyle mathcal L y y u ij epsilon ab h b dagger overline Q ia u j c y d ij h overline Q i d j c y e ij h overline L i e j c h c Elektrozayif simetrinin bozulmasindan sonra Higgs beklenen bir vakum degerini elde ettikten sonra Lagrangian bunu tekrar tanimlar Karmasikligindan oturu Lagrangian asagidaki denkligi bircok parcaya ayirarak tanimlamistir LEW LK LN LC LH LHV LWWV LWWVV LY displaystyle mathcal L EW mathcal L K mathcal L N mathcal L C mathcal L H mathcal L HV mathcal L WWV mathcal L WWVV mathcal L Y Kinetik terim LK displaystyle mathcal L K Lagrangian in kismi turevler dinamik terimler ve kutle terimleri simetri bozulmadan once Lagrangian da yoktu gibi tum ikinci dereceden terimlerini icerir LK ff i mf f 14AmnAmn 12Wmn W mn mW2Wm W m 14ZmnZmn 12mZ2ZmZm 12 mH mH 12mH2H2 displaystyle begin aligned mathcal L K sum f overline f i partial m f f frac 1 4 A mu nu A mu nu frac 1 2 W mu nu W mu nu m W 2 W mu W mu qquad frac 1 4 Z mu nu Z mu nu frac 1 2 m Z 2 Z mu Z mu frac 1 2 partial mu H partial mu H frac 1 2 m H 2 H 2 end aligned toplam fermion teorisine gecer quarklar ve leptonlar alanlar Amn displaystyle A mu nu Zmn displaystyle Z mu nu Wmn displaystyle W mu nu and Wmn Wmn displaystyle W mu nu equiv W mu nu dagger and asagida verilir Xmn mXn nXm gfabcXmbXnc displaystyle X mu nu partial mu X nu partial nu X mu gf abc X mu b X nu c ilgili alani X ile yer degistirin ve ayar grubu icin yapi sabitleri fabc Lagrangian in bilesenleri notr akim ve yuklu akim fermionlar ve ayar bozonlari arasinda bir etkilesim icerir LN eJmemAm gcos 8W Jm3 sin2 8WJmem Zm displaystyle mathcal L N eJ mu em A mu frac g cos theta W J mu 3 sin 2 theta W J mu em Z mu Elektromanyetik akim Jmem displaystyle J mu em ve notr zayif akim Jm3 displaystyle J mu 3 dir Jmem fqff gmf displaystyle J mu em sum f q f overline f gamma mu f ve Jm3 fIf3f gm1 g52f displaystyle J mu 3 sum f I f 3 overline f gamma mu frac 1 gamma 5 2 f qf displaystyle q f ve If3 displaystyle I f 3 fermionlarin zayif esspin ve elektrik yukleridir Lagrangian in yuklu akim kismi soyledir LC g2 u igm1 g52MijCKMdj n igm1 g52ei Wm h c displaystyle mathcal L C frac g sqrt 2 left overline u i gamma mu frac 1 gamma 5 2 M ij CKM d j overline nu i gamma mu frac 1 gamma 5 2 e i right W mu h c LH displaystyle mathcal L H Higgs uc noktasi ve dort noktali kendi etkilesim terimini icerir LH gmH24mWH3 g2mH232mW2H4 displaystyle mathcal L H frac gm H 2 4m W H 3 frac g 2 m H 2 32m W 2 H 4 LHV displaystyle mathcal L HV ayar vektor bozonlari ile Higss etkilesimi icerir LHV gmWH g24H2 Wm W m 12cos2 8WZmZm displaystyle mathcal L HV left gm W H frac g 2 4 H 2 right left W mu W mu frac 1 2 cos 2 theta W Z mu Z mu right LWWV displaystyle mathcal L WWV uc noktali kendi etkilesim ayarlarini icerir LWWV ig Wmn W m W mWmn Ansin 8W Zncos 8W Wn Wm Amnsin 8W Zmncos 8W displaystyle mathcal L WWV ig W mu nu W mu W mu W mu nu A nu sin theta W Z nu cos theta W W nu W mu A mu nu sin theta W Z mu nu cos theta W LWWVV displaystyle mathcal L WWVV dort noktali kendi etkilesim ayarlarini icerir LWWVV g24 2Wm W m Amsin 8W Zmcos 8W 2 2 Wm Wn Wn Wm Amsin 8W Zmcos 8W Ansin 8W Zncos 8W 2 displaystyle begin aligned mathcal L WWVV frac g 2 4 Big amp 2W mu W mu A mu sin theta W Z mu cos theta W 2 2 amp W mu W nu W nu W mu A mu sin theta W Z mu cos theta W A nu sin theta W Z nu cos theta W 2 Big end aligned LY displaystyle mathcal L Y fermionlar ve Higgs alani arasinda Yukawa etkilesimlerini icerir LY fgmf2mWf fH displaystyle mathcal L Y sum f frac gm f 2m W overline f fH Zayif eslesmelerde 1 g52 displaystyle frac 1 gamma 5 2 faktorlerini not edin bu faktorler spinor alanlarinin sol el bilesenlerini yansitir Bu yuzden elektrozayif teoriye simetri bozulduktan sonra yaygin olarak kiral bakisimsiz teori de denmektedir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State