Eliptik Eğri Diffie-Hellman (ECDH), güvensiz bir kanal üzerinden paylaşılan bir giz (İngilizce: secret) oluşturmak için her biri eliptik-eğri açık-özel anahtar çiftine sahip iki partiye izin veren anonim bir anahtar anlaşma protokolüdür. Bu paylaşılan sır doğrudan bir anahtar olarak veya başka bir anahtar türetmek için kullanılabilir. Anahtar veya üretilen anahtar, daha sonra sonraki iletişimleri, bir simetrik anahtar algoritması kullanarak şifrelemek için kullanılabilir. Bu, Diffie-Hellman protokolünün eliptik eğri kriptografisi kullanan bir çeşididir.
Anahtar oluşturma protokolü
Sıradaki örnek anahtar oluşturulmasının nasıl yapıldığını açıklayacak. Diyelim ki Alice, Bob ile paylaşılan bir anahtar oluşturmak istiyor,ama ikisi için uygun olan tek kanal, üçüncü bir parti tarafından gizlice dinlenebilir. Başlangıçta, etki alanı parametreleri (yani, asal durumda 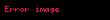

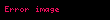
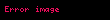

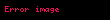

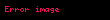
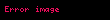
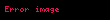
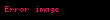
Alice 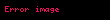
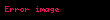
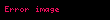
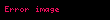
İki tarafın da hesapladığı paylaşılan giz eşittir, çünkü 
Alice’in başlangıçta açıkladığı özel anahtarı hakkında tek bilgi açık anahtarıdır. Yani, Alice’ten başka hiçbir parti, eliptik eğri ayrık logaritma problemini çözmedikçe Alice’in özel anahtarına karar veremez. Bob’un özel anahtarı da aynı şekilde güvendedir. Alice ve Bob’dan başka hiçbir parti, eliptik eğri Diffie-Hellman problemini çözmedikçe paylaşılan secreti hesaplayamaz.
Açık anahtarlar ya statiktir (ve güvenilirdir, mesela bir sertifika aracılığıyla) ya da geçicidirler (ECDHE olarak da bilinir, son E'nin "geçici" anlamına gelen "ephemeral"in baş harfidir.). Geçici anahtarlar geçicidir ve kimlik doğrulamasına gerek yoktur, yani eğer kimlik doğrulaması yapmak istenirse, authenticity başka yollarla sağlanmalıdır. Kimlik doğrulaması, ortadaki adam saldırılarından korunmak için gereklidir. Eğer Alice veya Bob’dan birinin açık anahtarı statik ise, ortadaki adam saldırıları önlenmiştir. Statik açık anahtarlar, diğer gelişmiş güvenlik özelliklerindenileriye dönük gizlilik (İngilizce: forward secrecy) veya anahtar-uzlaşma kimliğe bürünme esnekliği (İngilizce: key-compromise impersonation resilience) sağlamaz. Statik özel anahtarı olanlar, diğer açık anahtarı doğrulamalı ve statik özel anahtarla ilgili bilgi sızdırmamak için ham Diffie-Hellman paylaşılan gizine güvenli bir anahtar türetme fonksiyonu uygulamalıdır. Diğer güvenlik özelliklerine sahip programlar için MQV'ye bakınız.
Paylaşılan bir giz doğrudan bir anahtar olarak kullanılabilir, genelde Diffie-Hellman değişiminden kaynaklanan zayıf bitleri ortadan kaldırmak için gizi hashlemek tercih edilir.
- Curve25519, eliptik eğri parametreleri kümesidir ve C [./https://en.wikipedia.org/wiki/Language_binding 14 Nisan 2019 tarihinde Wayback Machine sitesinde arşivlendi. Bindings]'deki Daniel J. Bernsteintarafından yapılan referans gerçeklemesi ve alternatif gerçeklemeler de mevcuttur.
- LINE messenger uygulaması, ECDH protokolünü Ekim 2015'ten bu yana, söz konusu uygulama aracılığıyla gönderilen tüm iletilerin "Letter Sealing" uçtan uca şifrelemesi için kullanmıştır.
Ayrıca bakınız
Kaynakça
- ^ NIST, Özel Yayın 800-56A, Kesikli Logaritma Şifrelemesi Kullanarak Çift Anahtarlı Anahtar Kuruluş Şemaları için Tavsiye 14 Temmuz 2007 tarihinde Wayback Machine sitesinde ., Mart 2006.
- ^ Certicom Research, Etkili şifreleme standartları, SEC 1: Eliptik Eğri Şifreleme 11 Kasım 2014 tarihinde Wayback Machine sitesinde ., Versiyon 2.0, 21 Mayıs 2009.
- ^ NSA Suite B Şifreleme, Suite B Uygulayıcıların NIST SP 800-56A Kılavuzu 6 Mart 2016 tarihinde Wayback Machine sitesinde ., 28 Temmuz 2009.
- ^ Tibor Jager; Jorg Schwenk; Juraj Somorovsky (4 Eylül 2015). (PDF). European Symposium on Research in Computer Security (ESORICS'15). 5 Ağustos 2019 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 15 Mart 2020.
- ^ JI (13 Ekim 2015). . LINE Engineers' Blog. LINE Corporation. 1 Şubat 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 15 Mart 2020.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Eliptik Egri Diffie Hellman ECDH guvensiz bir kanal uzerinden paylasilan bir giz Ingilizce secret olusturmak icin her biri eliptik egri acik ozel anahtar ciftine sahip iki partiye izin veren anonim bir anahtar anlasma protokoludur Bu paylasilan sir dogrudan bir anahtar olarak veya baska bir anahtar turetmek icin kullanilabilir Anahtar veya uretilen anahtar daha sonra sonraki iletisimleri bir simetrik anahtar algoritmasi kullanarak sifrelemek icin kullanilabilir Bu Diffie Hellman protokolunun eliptik egri kriptografisi kullanan bir cesididir Anahtar olusturma protokoluSiradaki ornek anahtar olusturulmasinin nasil yapildigini aciklayacak Diyelim ki Alice Bob ile paylasilan bir anahtar olusturmak istiyor ama ikisi icin uygun olan tek kanal ucuncu bir parti tarafindan gizlice dinlenebilir Baslangicta etki alani parametreleri yani asal durumda p a b G n h displaystyle p a b G n h p a b G n h displaystyle p a b G n h p a b G n h displaystyle p a b G n h p a b G n h displaystyle p a b G n h p a b G n h textstyle p a b G n h p a b G n h displaystyle p a b G n h p a b G n h displaystyle p a b G n h veya ikilik taban durumunda m f x a b G n h textstyle m f x a b G n h m f x a b G n h displaystyle m f x a b G n h konusunda anlasma saglanmalidir Ayrica her partinin eliptik egri kriptografisine uygun ozel anahtar d textstyle d 1 n 1 textstyle 1 n 1 araligindan rastgele secilmis bir tam sayi ve bir Q textstyle Q noktasi Q dG textstyle Q dG yani G textstyle G nin kendisine d textstyle d defa eklendiginde cikan sonuc ile gosterilen bir acik anahtardan olusan bir anahtar cifti olmalidir Alice in anahtar cifti dA QA displaystyle d A Q A Bob un anahtar cifti dB QB displaystyle d B Q B olsun Her parti diger partinin protokol calistirilmadan onceki acik anahtarini bilmelidir Alice xk yk dAQB displaystyle x k y k d A Q B noktasini hesaplar Bob xk yk dBQA displaystyle x k y k d B Q A noktasini hesaplar Paylasilan giz Ingilizce secret xk displaystyle x k dir noktanin x koordinati ECDH e dayali en standart hale getirilmis protokoller hash tabanli anahtar uretim fonksiyonu kullanarak xk displaystyle x k dan simetrik anahtar uretir Iki tarafin da hesapladigi paylasilan giz esittir cunku dAQB dAdBG dBdAG dBQA displaystyle d A Q B d A d B G d B d A G d B Q A dAQB dAdBG dBdAG dBQA displaystyle d A Q B d A d B G d B d A G d B Q A dir Alice in baslangicta acikladigi ozel anahtari hakkinda tek bilgi acik anahtaridir Yani Alice ten baska hicbir parti eliptik egri ayrik logaritma problemini cozmedikce Alice in ozel anahtarina karar veremez Bob un ozel anahtari da ayni sekilde guvendedir Alice ve Bob dan baska hicbir parti eliptik egri Diffie Hellman problemini cozmedikce paylasilan secreti hesaplayamaz Acik anahtarlar ya statiktir ve guvenilirdir mesela bir sertifika araciligiyla ya da gecicidirler ECDHE olarak da bilinir son E nin gecici anlamina gelen ephemeral in bas harfidir Gecici anahtarlar gecicidir ve kimlik dogrulamasina gerek yoktur yani eger kimlik dogrulamasi yapmak istenirse authenticity baska yollarla saglanmalidir Kimlik dogrulamasi ortadaki adam saldirilarindan korunmak icin gereklidir Eger Alice veya Bob dan birinin acik anahtari statik ise ortadaki adam saldirilari onlenmistir Statik acik anahtarlar diger gelismis guvenlik ozelliklerindenileriye donuk gizlilik Ingilizce forward secrecy veya anahtar uzlasma kimlige burunme esnekligi Ingilizce key compromise impersonation resilience saglamaz Statik ozel anahtari olanlar diger acik anahtari dogrulamali ve statik ozel anahtarla ilgili bilgi sizdirmamak icin ham Diffie Hellman paylasilan gizine guvenli bir anahtar turetme fonksiyonu uygulamalidir Diger guvenlik ozelliklerine sahip programlar icin MQV ye bakiniz Paylasilan bir giz dogrudan bir anahtar olarak kullanilabilir genelde Diffie Hellman degisiminden kaynaklanan zayif bitleri ortadan kaldirmak icin gizi hashlemek tercih edilir Curve25519 eliptik egri parametreleri kumesidir ve C https en wikipedia org wiki Language binding 14 Nisan 2019 tarihinde Wayback Machine sitesinde arsivlendi Bindings deki Daniel J Bernsteintarafindan yapilan referans gerceklemesi ve alternatif gerceklemeler de mevcuttur LINE messenger uygulamasi ECDH protokolunu Ekim 2015 ten bu yana soz konusu uygulama araciligiyla gonderilen tum iletilerin Letter Sealing uctan uca sifrelemesi icin kullanmistir Ayrica bakinizDiffie Hellman anahtar degisimiKaynakca NIST Ozel Yayin 800 56A Kesikli Logaritma Sifrelemesi Kullanarak Cift Anahtarli Anahtar Kurulus Semalari icin Tavsiye 14 Temmuz 2007 tarihinde Wayback Machine sitesinde Mart 2006 Certicom Research Etkili sifreleme standartlari SEC 1 Eliptik Egri Sifreleme 11 Kasim 2014 tarihinde Wayback Machine sitesinde Versiyon 2 0 21 Mayis 2009 NSA Suite B Sifreleme Suite B Uygulayicilarin NIST SP 800 56A Kilavuzu 6 Mart 2016 tarihinde Wayback Machine sitesinde 28 Temmuz 2009 Tibor Jager Jorg Schwenk Juraj Somorovsky 4 Eylul 2015 PDF European Symposium on Research in Computer Security ESORICS 15 5 Agustos 2019 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 15 Mart 2020 JI 13 Ekim 2015 LINE Engineers Blog LINE Corporation 1 Subat 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 15 Mart 2020
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
