Öklid geometrisinde, Erdős–Mordell eşitsizliği herhangi bir üçgeni ve içindeki noktası için, 'den kenarlara olan uzunlukların toplamının, 'den köşelere olan uzunlukların toplamının yarısına eşit veya daha az olduğunu belirten teoremdir. Teorem, adını Macar matematikçi Paul Erdős ve Amerika doğumlu İngiliz matematikçi 'den almıştır. Erdős (1935) eşitsizliği kanıtlama problemini ortaya attı; iki yıl sonra (Louis Mordell & D. F. Barrow 1937) tarafından bir kanıt sağlandı. Ancak bu çözüm çok basit değildi. Sonraki basit ispatlar daha sonra Kazarinoff (1957), Bankoff (1958) ve Alsina & Nelsen (2007) tarafından verilmiştir.
Barrow eşitsizliği, 'den kenarlara olan uzunlukların 'den , ve açıortaylarının kenarları kestiği noktalara kadar olan uzunlukları ile değiştirildiği Erdős–Mordell eşitsizliğinin güçlendirilmiş bir versiyonudur. Değiştirilen uzunluklar daha uzun olmasına rağmen, bunların toplamı yine de köşelere olan uzunlukların toplamının yarısından daha az veya buna eşittir.
Açıklama



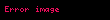



İspat










.
Bu aşağıdaki ifadeye eşdeğerdir:
.
Sağ taraf 



,
,
.
Üç ifadeyi birbirine ekleyerek,
bulunur. Pozitif bir sayının toplamı ve çarpmaya göre tersinin göre en az 2 olması nedeniyle, teorem ispatlanmış olur. Eşitlik yalnızca eşkenar üçgen için geçerlidir ve bu durumda 
Başka bir güçlendirilmiş versiyon











yazılabilir. Eşitlik ancak ve ancak 
Bir genelleme



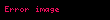

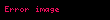







olarak yazılabilir.
Ayrıca bakınız
Kaynakça
- Alsina, Claudi; Nelsen, Roger B. (2007), "A visual proof of the Erdős-Mordell inequality", Forum Geometricorum, cilt 7, ss. 99-102, 16 Temmuz 2020 tarihinde kaynağından , erişim tarihi: 26 Kasım 2020.
- (1958), "An elementary proof of the Erdős-Mordell theorem", , 65 (7), s. 521, doi:10.2307/2308580, JSTOR 2308580.
- Dao, Thanh Oai; Nguyen, Tien Dung; Pham, Ngoc Mai (2016), "A strengthened version of the Erdős-Mordell inequality" (PDF), Forum Geometricorum, cilt 16, ss. 317-321, MR 3556993, 24 Nisan 2018 tarihinde kaynağından (PDF), erişim tarihi: 26 Kasım 2020.
- Erdős, Paul (1935), "Problem 3740", , cilt 42, s. 396, doi:10.2307/2301373.
- Kazarinoff, D. K. (1957), "A simple proof of the Erdős-Mordell inequality for triangles", , 4 (2), ss. 97-98, doi:10.1307/mmj/1028988998.
- Lenhard, Hans-Christof (1961), "Verallgemeinerung und Verschärfung der Erdös-Mordellschen Ungleichung für Polygone", Archiv für Mathematische Logik und Grundlagenforschung, cilt 12, ss. 311-314, doi:10.1007/BF01650566, MR 0133060.
- Marinescu, Dan Ștefan; Monea, Mihai (2017), "About a strengthened version of the Erdős-Mordell inequality" (PDF), Forum Geometricorum, cilt 17, ss. 197-202, 24 Nisan 2018 tarihinde kaynağından (PDF), erişim tarihi: 26 Kasım 2020.
- ; (1937), "Solution to 3740", , cilt 44, ss. 252-254, doi:10.2307/2300713.
Dış bağlantılar
- Eric W. Weisstein, Erdős-Mordell Theorem (MathWorld)
- , "Erdös-Mordell Inequality 6 Ağustos 2020 tarihinde Wayback Machine sitesinde ." @ Cut-the-Knot.
- Erdős-Mordell @ Geogebra
Konuyla ilgili yayınlar
- Kazarinoff, Donat K. A simple proof of the Erdős-Mordell inequality for triangles. Michigan Math. J. 4 (1957), No. 2, ss. 97-98, doi:10.1307/mmj/1028988998. Makale 19 Haziran 2020 tarihinde Wayback Machine sitesinde .
- Seannie Dar & Shay Gueron, A Weighted Erdös-Mordell Inequality, The American Mathematical Monthly Vol. 108, No. 2 (Feb., 2001), ss. 165-168, https://doi.org/10.2307/2695531, Makale
- Liu, Jian and Zhang, Zhi-Hua (2004), An Erdös-Mordell Type Inequality on the Triangle, Araştırma Raporu 30 Eylül 2019 tarihinde Wayback Machine sitesinde .
- Yu-Dong Wu, Chun-Lei Yu & Zhi-Hua Zhang, (2009), A Geometric Inequality of the Generalized Erdös-Mordell Type, Journal of Inequalities in Pure and Alliped Mathematics, issn: 1443-5756, Volume 10 (2009), Issue 4, Article 106, ss. 1-5, Makale 7 Temmuz 2020 tarihinde Wayback Machine sitesinde .
- Liu, J., (2011), A New Proof of the Erdos-Mordell Inequality. International Electronic Journal of Geometry 4, ss. 114-119, Makale
- Jian Liu, (2015), Sharpened versions of the Erdös-Mordell inequality, Journal of Inequalities and Applications, 2015:206, doi:10.1186/s13660-015-0716-2, Makale 17 Kasım 2019 tarihinde Wayback Machine sitesinde .
- Liu, Jian. (Apr 2018), Two New Weighted Erdős–Mordell Type Inequalities, Discrete & Computational Geometry; New York, Vol. 59, Issue: 3, ss. 707-724, doi:10.1007/s00454-017-9917-4
- Jian Liu, (2019), New Refinements of the Erdös–Mordell Inequality and Barrow’s Inequality, Mathematics 2019, 7(8), 726; https://doi.org/10.3390/math7080726
- Maja Petrovic, Branko Malesevic, Bojan Banjac, (2019), On the Erdos-Mordell Inequality for Triangles in Taxicab Geometry, Makale
- George Tsintsifas, The Erdos-Mordell inequality, Makale
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Oklid geometrisinde Erdos Mordell esitsizligi herhangi bir ABC displaystyle triangle ABC ucgeni ve ABC displaystyle triangle ABC icindeki P displaystyle P noktasi icin P displaystyle P den kenarlara olan uzunluklarin toplaminin P displaystyle P den koselere olan uzunluklarin toplaminin yarisina esit veya daha az oldugunu belirten teoremdir Teorem adini Macar matematikci Paul Erdos ve Amerika dogumlu Ingiliz matematikci den almistir Erdos 1935 esitsizligi kanitlama problemini ortaya atti iki yil sonra Louis Mordell amp D F Barrow 1937 tarafindan bir kanit saglandi Ancak bu cozum cok basit degildi Sonraki basit ispatlar daha sonra Kazarinoff 1957 Bankoff 1958 ve Alsina amp Nelsen 2007 tarafindan verilmistir Barrow esitsizligi P displaystyle P den kenarlara olan uzunluklarin P displaystyle P den APB displaystyle angle APB BPC displaystyle angle BPC ve CPA displaystyle angle CPA aciortaylarinin kenarlari kestigi noktalara kadar olan uzunluklari ile degistirildigi Erdos Mordell esitsizliginin guclendirilmis bir versiyonudur Degistirilen uzunluklar daha uzun olmasina ragmen bunlarin toplami yine de koselere olan uzunluklarin toplaminin yarisindan daha az veya buna esittir AciklamaErdos Mordell esitsizligi P displaystyle P verilen bir ABC displaystyle triangle ABC ucgeni icerisinde keyfi bir nokta ve PL displaystyle PL PM displaystyle PM PN displaystyle PN ise P displaystyle P den ucgenlerin kenarlarina cizilen dikmeler olsun Ucgen genis acili ise bu diklerden biri ucgenin farkli bir kenarindan gecebilir ve kenarlardan birini destekleyen yani disa dogru uzatilan dogruda bitebilir Sonra soz konusu esitsizlik asagidaki sekilde ifade edilir PA PB PC 2 PL PM PN displaystyle PA PB PC geq 2 PL PM PN Ispat ABC displaystyle triangle ABC ucgeninin kenarlari a A displaystyle A kosesinin karsisinda b B displaystyle B kosesinin karsisinda ve c C displaystyle C kosesinin karsisinda olsun ayni zamanda PA p displaystyle PA p PB q displaystyle PB q PC r displaystyle PC r uzunluk P BC x displaystyle uzunluk P BC x uzunluk P CA y displaystyle uzunluk P CA y uzunluk P AB z displaystyle uzunluk P AB z olsun Ilk once asagidaki ifadeyi kanitliyoruz cr ax by displaystyle cr geq ax by Bu asagidaki ifadeye esdegerdir c r z 2 ax by cz2 displaystyle frac c r z 2 geq frac ax by cz 2 Sag taraf ABC displaystyle triangle ABC ucgeninin alanidir ancak sol tarafta r z en azindan ucgenin yuksekligidir sonuc olarak sol taraf sag taraftan daha kucuk olamaz Simdi P displaystyle P nin C displaystyle C deki aciortaya gore simetrisini alalim P displaystyle P nin yansimasi icin cr ay bx oldugunu buluruz Benzer sekilde bq az cx ve ap bz cy oldugu gorulur Bu esitsizlikleri r q ve p icin cozersek r a c y b c x displaystyle r geq a c y b c x q a b z c b x displaystyle q geq a b z c b x p b a z c a y displaystyle p geq b a z c a y Uc ifadeyi birbirine ekleyerek p q r bc cb x ac ca y ab ba z displaystyle p q r geq left frac b c frac c b right x left frac a c frac c a right y left frac a b frac b a right z bulunur Pozitif bir sayinin toplami ve carpmaya gore tersinin gore en az 2 olmasi nedeniyle teorem ispatlanmis olur Esitlik yalnizca eskenar ucgen icin gecerlidir ve bu durumda P displaystyle P merkez noktasidir Baska bir guclendirilmis versiyon ABC displaystyle triangle ABC bir O displaystyle O cemberi icine cizilmis bir ucgen ve P displaystyle P ABC displaystyle triangle ABC nin icindeki bir nokta olsun D E F displaystyle D E F ise P displaystyle P noktasinin BC CA AB displaystyle BC CA AB kenarlari uzerine dik izdusumleri olsun M N Q displaystyle M N Q P displaystyle P noktasinin sirasiyla A B C displaystyle A B C de O displaystyle O ya tegetlere dik izdusumleri olabilir o zaman PM PN PQ 2 PD PE PF displaystyle PM PN PQ geq 2 PD PE PF yazilabilir Esitlik ancak ve ancak ABC displaystyle triangle ABC ucgeni eskenar ise gecerlidir Dao Nguyen amp Pham 2016 Marinescu amp Monea 2017 Bir genellemeA1A2 An displaystyle A 1 A 2 A n disbukey bir cokgen ve P displaystyle P A1A2 An displaystyle A 1 A 2 A n nin bir ic noktasi olsun Ri displaystyle R i P displaystyle P noktasindan Ai displaystyle A i tepe noktasina olan uzaklik ri displaystyle r i P displaystyle P noktasindan AiAi 1 displaystyle A i A i 1 kenarina olan uzaklik wi displaystyle w i P displaystyle P noktasindan AiAi 1 displaystyle A i A i 1 kenariyla kesisme noktasina kadar olan AiPAi 1 displaystyle A i PA i 1 acisinin aciortay segmenti olsun sonra Lenhard 1961 i 1nRi sec pn i 1nwi sec pn i 1nri displaystyle sum i 1 n R i geq left sec frac pi n right sum i 1 n w i geq left sec frac pi n right sum i 1 n r i olarak yazilabilir Ayrica bakinizKaynakcaAlsina Claudi Nelsen Roger B 2007 A visual proof of the Erdos Mordell inequality Forum Geometricorum cilt 7 ss 99 102 16 Temmuz 2020 tarihinde kaynagindan erisim tarihi 26 Kasim 2020 1958 An elementary proof of the Erdos Mordell theorem 65 7 s 521 doi 10 2307 2308580 JSTOR 2308580 Dao Thanh Oai Nguyen Tien Dung Pham Ngoc Mai 2016 A strengthened version of the Erdos Mordell inequality PDF Forum Geometricorum cilt 16 ss 317 321 MR 3556993 24 Nisan 2018 tarihinde kaynagindan PDF erisim tarihi 26 Kasim 2020 Erdos Paul 1935 Problem 3740 cilt 42 s 396 doi 10 2307 2301373 Kazarinoff D K 1957 A simple proof of the Erdos Mordell inequality for triangles 4 2 ss 97 98 doi 10 1307 mmj 1028988998 Lenhard Hans Christof 1961 Verallgemeinerung und Verscharfung der Erdos Mordellschen Ungleichung fur Polygone Archiv fur Mathematische Logik und Grundlagenforschung cilt 12 ss 311 314 doi 10 1007 BF01650566 MR 0133060 Marinescu Dan Ștefan Monea Mihai 2017 About a strengthened version of the Erdos Mordell inequality PDF Forum Geometricorum cilt 17 ss 197 202 24 Nisan 2018 tarihinde kaynagindan PDF erisim tarihi 26 Kasim 2020 1937 Solution to 3740 cilt 44 ss 252 254 doi 10 2307 2300713 Dis baglantilarEric W Weisstein Erdos Mordell Theorem MathWorld Erdos Mordell Inequality 6 Agustos 2020 tarihinde Wayback Machine sitesinde Cut the Knot Erdos Mordell GeogebraKonuyla ilgili yayinlarKazarinoff Donat K A simple proof of the Erdos Mordell inequality for triangles Michigan Math J 4 1957 No 2 ss 97 98 doi 10 1307 mmj 1028988998 Makale 19 Haziran 2020 tarihinde Wayback Machine sitesinde Seannie Dar amp Shay Gueron A Weighted Erdos Mordell Inequality The American Mathematical Monthly Vol 108 No 2 Feb 2001 ss 165 168 https doi org 10 2307 2695531 Makale Liu Jian and Zhang Zhi Hua 2004 An Erdos Mordell Type Inequality on the Triangle Arastirma Raporu 30 Eylul 2019 tarihinde Wayback Machine sitesinde Yu Dong Wu Chun Lei Yu amp Zhi Hua Zhang 2009 A Geometric Inequality of the Generalized Erdos Mordell Type Journal of Inequalities in Pure and Alliped Mathematics issn 1443 5756 Volume 10 2009 Issue 4 Article 106 ss 1 5 Makale 7 Temmuz 2020 tarihinde Wayback Machine sitesinde Liu J 2011 A New Proof of the Erdos Mordell Inequality International Electronic Journal of Geometry 4 ss 114 119 Makale Jian Liu 2015 Sharpened versions of the Erdos Mordell inequality Journal of Inequalities and Applications 2015 206 doi 10 1186 s13660 015 0716 2 Makale 17 Kasim 2019 tarihinde Wayback Machine sitesinde Liu Jian Apr 2018 Two New Weighted Erdos Mordell Type Inequalities Discrete amp Computational Geometry New York Vol 59 Issue 3 ss 707 724 doi 10 1007 s00454 017 9917 4 Jian Liu 2019 New Refinements of the Erdos Mordell Inequality and Barrow s Inequality Mathematics 2019 7 8 726 https doi org 10 3390 math7080726 Maja Petrovic Branko Malesevic Bojan Banjac 2019 On the Erdos Mordell Inequality for Triangles in Taxicab Geometry Makale George Tsintsifas The Erdos Mordell inequality Makale
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans











