Bu madde, uygun değildir. (Aralık 2017) |
Modern kuantum (nicem) mekaniğinden önce gelen eski kuantum (nicem) kuramı, 1900 ile 1925 yılları arasında elde edilen sonuçların birikimidir. Bu kuramın, klasik mekaniğin ilk doğrulamaları olduğunu günümüzde anladığımız bu kuram, ilk zamanlar tamamlanmış veya istikrarlı değildi. Bohr modeli çalışmaların odak noktasıydı. Eski kuantum döneminde, Arnold Sommerfield, uzay nicemlenimi olarak anılan açısal momentumun (devinimin) z-bileşkesinde nicemlenim yaparak önemli katkılarda bulunmuştur. Bu katkı, electron yörüngelerinin dairesel yerine eliptik olduğunu ortaya çıkarmıştır ve kuantum çakışıklık kavramını ortaya atmıştır. Bu kuram, electron dönüsü hariç Zeeman etkisini açıklamaktadır.
Ana araç Bohr-Sommerfeld kuantizasyonudur (nicemlenimidir). Bu da izin verilen durumlarda klasik tümlevlenebilir hareketin durumlarının belirli ayrık takımlarını seçme prosedürüdür. Bunlar Bohr atom modelinde izin verilen yörüngeler gibidir. Bu kuram kaotik hareketleri genişletmemektedir.
Temel İlkeler
Eski kuantum kuramındaki temel fikir, nicemlenmiş veya ayrık bir atomik sistemdeki harekettir. Bu sistem bütün hareketler hariç olmak üzere klasik mekaniğe uymaktadır. Eski kuantum kuramına uyan hareketler;
Denklemde, 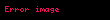


Eski kuantum durumlarının bir anlam ifade edebilmesi için klasik hareketin ayırt edilebilir olması gerekmektedir. Bunun anlamı 
Eski kuantumum şartı karşılılık ilkesidir. Fiziksel gözlemler göstermiştir ki nicemlenmiş miktar adiyabatik değişmiş olmalıdır. Uyumlu salıngaç için geçerli olan Planck nicemlenimi (kuantizasyonu) kuralı, genel bir sistemde, toplanır sabite kadar olan herhangi bir durumu doğrular nitelikte olan klasik bir değeri nicemler.
Örnekler
Uyumlu Salıngaç (Harmonik Osilatör)
Eski kuantum kuramındaki en basit sistem uyumlu (harmonic) salıngaçdır. Bunun Hamiltonyan'ı;
Bu denklemde, 
Bu sonuç önceden de oldukça iyi bilinmekteydi ve eski kuantum şartını formülize etmek için kullanılmıştır. Bu sonuç kuantum mekaniğinin yardımlarıyla bulunan 
Nicemlenmiş bir salıngaçın (osilatörün) ısısal (termal) özellikleri Boltzmann ağırlığı ile bağlanmış olduğunu varsaydığımız her bir ayrık durgunun emerjilerinin ortalaması alınarak bulunabilir.
Bu denklemde 


Bu ifadeden anlaşılacağı üzere, kolaylıkla görülür ki büyük 


Küçük 

Oda sıcaklığında, tek atomlu katılar yaklaşık olarak atom başına 3k ile aynı öz ısıya sahiptirler. Fakat bu durum düşük sıcaklıklarda geçerli değildir. Daha düşük sıcaklıklarda öz ısı da daha küçüktür ve sıfıra doğru gitmektedir. Bu bütün materyal sistemleri için doğrudur ve bu gözlem termodinamiğin üçüncü yasası olarak bilinir. Klasik mekanik üçüncü yasayı açıklayamaz çünkü klasik mekanikde öz ısı sıcaklıktan bağımsızdır.
Klasik mekanik ve soğuk malzemelerin öz ısısı arasındaki bu çelişkiyi 19.yüzyılda James Clerk Maxwell dikkate almıştır. 1906’da Albert Einstein bu problemi atomic hareketin nicemlenmiş olduğunu ileri sürerek yeniden çözmüştür. Bu kuantum kuramının mekanik sistemlere uyarlanmış ilk uygulamasaydı.
Çok kısa bir süre sonra, Peter Debye katıların öz ısıları hakkında ortaya nicel bir kuram sunmuştur.
Tek Boyutlu Potansiyel (Gerilim): U=0
Tek boyutlu problemlerin oldukça basittir. Herhangi bir 

Momentumun (Devinimin) ortadan kaybolduğu yerde, klasik dönüm noktaları arasındaki bütün 

Bu formül bize momentumu da vermektedir;
Ve son olarak enerji seviyeleri
Tek Boyutlu Potansiyel (Gerilim): U=Fx
Eski kuantum kuramı ile kolayca çözülebilen bir başka husus ise pozitif (artı) yarı yoldaki doğrusal gerilimdir (lineer potansiyel). Buradaki olay girilemez bir duvara sabit ve sınırlı bir 
dolayısıyla kuantum durumu şu şekilde olur;
Bu denklem enerji seviyelerini açıklar;
F=mg özel durumunda ise parçacık dünyanın yerçekimi potansiyeli tarafından sınırlandırılmıştır. Ayrıca burada "duvar" olarak yeryüzü kastedilmektedir.
Döner (Rotator)
Bir başka basit sistem ise dönerdir. Bir döner, iki boyutta kütlesiz R uzunluğundaki sabit bir çubuğun ucunda M kadar kütle ihtiva ettiğinde, bu dönerin Lagrangian'ı;
olur ve bu denklem polar (kutuplu) 
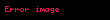



Bohr modelinde bu kısıtlama dairesel yörüngelerde bulunan enerji seviyelerini açıklamayı zorlamaktadır.
3 boyutta sabit bir döner 



Bu durumda eşlenik momentum 



olur ki bu da z bileşkesinin açısal momentumudur. Kuantum durumu 



Burada m manyetik (mıknatısal duygunluk) kuantum sayısı olarak anılır çünkü açısal momentumun z bileşkesi, z ekseni boyunca dönerin manyetik momentumudur. Bu eşitlik dönerin sonunda bulunan parçacığın yüklenmiş durumlarda geçerlidir.
3 boyutlu döner bir eksen etrafında döndüğü için toplam açısal momentum, 2 boyutlu dönerde olduğu gibi sınırlandırılmalıdır.İki kuantum durumunda toplam açısal momentumu ve 
Bu fenomen bir eksen etrafında bulunan açısal momentumun kuantize edilmesi "boşluk kuantizasyonu" olarak adlandırılmıştır çünkü bu durum rotasyonel (dönüşsel) değişmezlik ile uyumsuz görünmüştür. Modern kuantum mekaniğinde açısal momentum aynı şekilde kuantize edilir fakat herhangi bir yöndeki açısal momentumun ayrık durumları diğer yönlerdeki durumların kuantum süper pozisyonudur (üstdüşümüdür). Dolayısıyla kuantizasyonun işlem süreci tercih edilen bir eksen çıkarmamaktadır. Bu nedenle "boşluk kuantizasyonu" ismi gözden düşmüş, onun yerine bu fenomen "açısal momentum kuantizasyonu" olarak anılmaya başlamıştır.
Hidrojen Atomu
Hidrojen atomunun açısal bölümü sadece bir dönerden (rotator) ibarettir ve bu bize kuantum numaraları olan 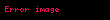


Enerjiyi sabit bir değere oturtmak ve 
Bu yalın bir denklemdir ve bize 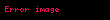

Bu durumda enerjinin formülü aşağıdaki gibi olmaktadır:
Bu formül asıl kuantum sayısı 




Kısmen klasik olan hidrojen atomu Sommerfeld modeli olarak adlandırılır ve ayrık eğimlerde bu atomun yörüngeleri farklı ölçülerde ve eliptik olur. Sommerfeld modelinin tahminine göre bir atomun manyetik momentu ancak ayrık değerler alacak bir eksen boyunca ölçülebilir. Bunun ışığında yapılan ölçümler sonucu elde edilen bir sonuç rotasyonal değişmezlik ile çelişkili görünmüştür ama bu sonuç Stern-Gerlach deneyi ile onaylanmıştır. Bohr-Sommerfeld kuramı kuantum mekaniğin gelişiminin bir parçasıdır ve atomik enerji seviyelerinin manyetik alanlar tarafından yarılma ihtimalini tanımlayabilmektedir.
Relativistik (Göreli) Yörünge
Arnold Sommerfeld atomik enerji seviyelerinin relativistik (göreli) çözümlerini türeten kişidir. Bu türetmeye elektrik potansiyeldeki (gerilim) enerji için relativistik denklemle başlamak gerekmektedir;

Momentum için 


çözümüyle
Enberi noktasının (periapsis) açısal kayması devir başına şu şekilde olur;
Kuantum durumu ile ele aldığımızda
ve
Buradan enerjileri tanımlayabiliriz;
Bu denklemde 
De Broglie Dalgaları
1905 yılında, Einstein kısa dalga boyları için kutu içinde kuantize olmuş elektromanyetik (akımmıknatısal) olan osilatörlerinin (salıngaç) entropisinin (dağıntı) bir gazın noktasal parçacıklarının entropisine eşit olduğunu belirtti. Noktasal parçacıkların sayısı kuantaların (nicem paketlerinin) sayısına eşittir. Einstein bu kuantaya erişilebilir nesneler, ışık parçacıkalrı gibi davranabileceğine kanaat getirdi ve foton (ışıncık) olarak adlandırdı. (bkz. sayfa 139/140).
Einstein'ın bu kuramsal argümanı termodinamiğe (ısıdevinimsel), durum numaralarını saymaya dayanıyordu ve tam olarak ikna edici değildi. Sonuç olarak Einstein'da ışığı hem parçacık hem de dalga olarak atfetmiştir. Daha açıkça 
ile her biri 
Fotonlar enerji gibi momentumada sahiptir ve momentum 

1924 yılında, Doktora adayı Louis de Broglie kuantum durumuna yeni bir yöntem önerdi. Elektronları da fotonlar gibi ilişkilere uyacak dalga şeklinde tanımlayabilmiştir;
veya dalga boyu 
Louis de Broglie sonrasında kuantum koşullarını şöyle belirtmiştir;
Klasik yörüngeyi takip eden dalga için faz değişimlerini sayar ve bu 
Örneğin, bir kutuda hapsedilmiş bir parçacık için bir durağan dalga duvarlarının arasındaki mesafenin iki katı dalga boyunun tam sayı katı olmak zorundadır. Bu şart aşağıdaki denklemle ifade edilir;
Dolayısıyla kuantize momentum;
olur. Eski kuantum enerji düzeylerini yeniden oluşturur.
Bu geliime Einstein tarafından daha matematiksel bir formda verilmiştir. Einstein dalgalar için faz fonskiyonunu (işlevini) şöyle belirtir:"Hamilton dahi dalga mekaniğinin kısa dalga boyu limiti (sınırı) için tanımladığı bir denklemi, mekanik bir sistemde Hamilton-Jacobi denklemlerinin çözümüyle tanımlamaktadır. Bu fikirler Schrödinger denkleminin keşfine yol açmıştır."
Kramers Geçiş Matrisi (Dizeyi)
Eski kuantum kuramı sadece periyodik olan hareket açı değişkenlerine ayrılmış özel mekanik sistemler için formüle edilmiştir. Işınım salınımı veya emilimiyle ilgilenmemişti. Yine de Hendrik Kramers emilim ve salınımın nasıl hesaplanması gerektiğini sezgisel olarak tanımlamıştır. Kramer, kuantum sisteminin yörüngelerinin Fourier analizlerinin yeni harmoniklerin yörünge frekanslarını katları şeklinde ayrıştırılmasıyla analiz edilmesini önermiştir.
İndeks (dizin) 






Kramers durumlar arası geçişi ışınımın klasik salınımına benzerliğini ki bu yörünge frekansının katlarındaki frekanslarda gerçekleşir, önermiştir. Işınım salınımının oranı 
Eski Kuantum Kuramının Sınırları
Eski kuantum kuramı bazı sınırlamalara sahiptir:
- Eski kuantum kuramı, spektral (tayfsal) çizgilerin şiddetlerini hesaplayamamıştır.
- Eski kuantum kuramı, müstesna Zeeman tesirini açıklayamamıştır. (Burada elektron spinleri göz ardı edilemez)
- Eski kuantum kuramı, kaotik sistemleri kuantize edemez. Yani hareketli sistemlerin yörüngeleri ne yakındır ne periyodiktir ne de analitik form oluşturabilir.
Bu, ünlü kütle çekimsel 3-parça problemine, klasik kaotik benzeri olan 2 elektronlu atom kadar kolay sistemler için dahi sorular ortya çıkarır.
Fakat bu, Zeeman etkisi ile tek elektrondan fazla elektronları bulunan atomları tanımlamak için kullanılabilir. Sonradan, eski kuantum kuramı aslında kaotik kuantum mekaniğinin kısmen klasik varsayımları olduğunu öne sürmüştür fakat bu sınırlar hala araştırılmaktadır.
Tarihi
Eski kuantum kuramı Max Planck tarafından ışığın salınımı ve soğurulması üzerine ortaya çıkarılmış ve Albert Einstein'ın katıların öz ısısı üzerine çalışmasından sonra dikkate alınmıştır. Einstein, daha sonradan Debye, atomların hareketinin kuantum prensiplerine uygulamış ve öz ısı anormalliklerini açıklamıştır. 1913 yılında, Bohr benzerlik prensibini tanımlamış ve çizgi tayfını açıklayan, hidrojen atomu modelini formüle etmek için kullanmıştır. Birkaç yıl içerisinde Arnold Sommerfeld gelişigüzel tümlevlenebilir sistemlerin Einstein ve Lorentz tarafından tanımlanmış kuantum sayılarının yalıtılmış değişmezliğinin prensiplerini kullanarak genişletmiştir. Sommerfeld modeli, modern kuantum mekaniğine Bohr'unkinden daha yakındır.
1910 ve 1920'li yıllar boyunca olduğu gibi birçok problem karışık sonuçlarla eski kuantum kuramı kullanılarak çözümlenmeye çalışılmıştır. Moleküler dönüşler ve titreşimler tayfı anlaşılmış ve elektron spinleri keşfedilmiştir. Bu yarım katlarda bulunan kuantum sayıları karmaşasına yol açmıştır. Max Planck sıfır nokta enerjisini tanımladı ve Arnold Sommerfeld relativistik hidrojen atomunu kısmen klasik olarak kuantize etmiştir. Hendrik Kramers, Stark etkisini açıkladı. Bose-Einstein'da fotonların doğru kuantum istatistiklerini verdi.
Kramers kuantum durumların hareketin Fourier bileşkesi cinsinden olanlarının arasındaki geçiş ihtimallerini hesaplamaya yönelik bir yönergede bulunmuştur. Bu fikir Werner Heisenberg'in işbirliği ile kısmen klasik matrise kadar genişletilmiştir. Unutulmamalıdır ki kısmen klasik matris atomik geçiş ihtimallerinin tanımına benzer. Heisenberg, bu matris mekaniğini yaratarak bütün kuantum kuramını bu geçiş matrisleri cinsinden yeniden formülize etmiştir.
1924 yılında, Louis de Broglie maddenin dalga kuramını ortaya sunmuştur. Bu kuram kısa süre sonra Albert Einstein tarafından madde dalgaları için kısmen klasik denklemler kullanılarak genişletilmiştir. 1926'da Erwin Schrödinger tamamıyla doğru olan bir kuantum mekaniksel dalga denklemi bulmuştur. Bu buluş eski kuantum kuramının başarılarını belirsizlik ve tutarsızlık olmaksızın yeniden sunmuştur. Schrödinger'in dalga mekaniği, Schrödinger ve diğer bilim insanları iki yöntemin aynı deneysel tesadüflere sahip olacağını kanıtlayana kadar matris mekaniğinden ayrı olarak gelişmiştir. Daha sonra Paul Dirac, 1926 yılında iki yönteminde daha kapsamlı bir yöntem olan dönüşüm kuramı ile elde edilebileceğini yazmıştır.
Kaynakça
- ^ ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. ss. 206. ISBN .
- ^ Sommerfeld, Arnold (1919). Atombau und Spektrallinien'. Braunschweig: Friedrich Vieweg und Sohn. ISBN .
- ^ Arnold Sommerfeld (1921). Atombau und Spektrallinien. Braunschweig. [1]
- ^ Ya I Granovski (2004). "Sommerfeld formula and Dirac's theory" (PDF). Physics-Uspekhi. 47 (5). ss. 523-524. Bibcode:2004PhyU...47..523G. doi:10.1070/PU2004v047n05ABEH001885.
- ^ Einstein, Albert (1905). (PDF). Annalen der Physik. 17 (6). ss. 132-148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. 9 Temmuz 2011 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 18 Şubat 2008.
- ^ Chaddha, G.S. (2006). Quantum Mechanics. New Dehli: New Age international. ss. 8-9. ISBN . 23 Temmuz 2014 tarihinde kaynağından . Erişim tarihi: 11 Haziran 2014.
- ^ E.A. Solov’ev, E. A. (2011). "Classical approach in atomic physics". European Physical Journal D. 65 (3). ss. 331-351. arXiv:1003.4387 $2. Bibcode:2011EPJD...65..331S. doi:10.1140/epjd/e2011-20261-6.
- ^ L.D. Landau, (1977). Quantum Mechanics: Non-Relativistic Theory. 3rd. Vol. 3. Pergamon Press. ISBN .
Konuyla ilgili yayınlar
- Thewlis, J., (Ed.) (1962). Encyclopaedic Dictionary of Physics.
- Pais, Abraham (1982). "Max Born's Statistical Interpretation of Quantum Mechanics" (PDF). Science. 218 (4578). ss. 1193-8. Bibcode:1982Sci...218.1193P. doi:10.1126/science.218.4578.1193. (PMID) 17802457. 2 Ağustos 2021 tarihinde kaynağından (PDF). Erişim tarihi: 11 Haziran 2014. Address to annual meeting of the Optical Society of America October 21, 1982 (Tucson AZ). Retrieved 2013-09-08.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Aralik 2017 Modern kuantum nicem mekaniginden once gelen eski kuantum nicem kurami 1900 ile 1925 yillari arasinda elde edilen sonuclarin birikimidir Bu kuramin klasik mekanigin ilk dogrulamalari oldugunu gunumuzde anladigimiz bu kuram ilk zamanlar tamamlanmis veya istikrarli degildi Bohr modeli calismalarin odak noktasiydi Eski kuantum doneminde Arnold Sommerfield uzay nicemlenimi olarak anilan acisal momentumun devinimin z bileskesinde nicemlenim yaparak onemli katkilarda bulunmustur Bu katki electron yorungelerinin dairesel yerine eliptik oldugunu ortaya cikarmistir ve kuantum cakisiklik kavramini ortaya atmistir Bu kuram electron donusu haric Zeeman etkisini aciklamaktadir Ana arac Bohr Sommerfeld kuantizasyonudur nicemlenimidir Bu da izin verilen durumlarda klasik tumlevlenebilir hareketin durumlarinin belirli ayrik takimlarini secme prosedurudur Bunlar Bohr atom modelinde izin verilen yorungeler gibidir Bu kuram kaotik hareketleri genisletmemektedir Temel IlkelerEski kuantum kuramindaki temel fikir nicemlenmis veya ayrik bir atomik sistemdeki harekettir Bu sistem butun hareketler haric olmak uzere klasik mekanige uymaktadir Eski kuantum kuramina uyan hareketler H p q Epidqi nih displaystyle oint limits H p q E p i dq i n i h Denklemde pi displaystyle p i sistemin momentum devinimi ve qi displaystyle q i de karsilik olan koordinatlardir konsayilardir Kuantum sayisi olan ni displaystyle n i bir tam sayidir ve sabit enerjili hareketin bir periyodunda tumlevlenir integrali alinir Bu tumlev faz uzayindaki etki olarak adlandirilan ve birimi Planck sabiti olan bir alandir Bu nedenle Planck sabiti kuantum etkisi olarak da gecmektedir Eski kuantum durumlarinin bir anlam ifade edebilmesi icin klasik hareketin ayirt edilebilir olmasi gerekmektedir Bunun anlami qi displaystyle q i ayrik koordinatlarinin hareketinin periyodik oldugudur Farkli hareketlerin periyotlarinin ayni olmasi gibi bir zorunluluk yoktur Hatta bu hareketler kiyaslanamaz bile olabilir Fakat coklu periyodik yontemde hareketi curuten bir grup koordinat olmak zorundadir Eski kuantumum sarti karsililik ilkesidir Fiziksel gozlemler gostermistir ki nicemlenmis miktar adiyabatik degismis olmalidir Uyumlu salingac icin gecerli olan Planck nicemlenimi kuantizasyonu kurali genel bir sistemde toplanir sabite kadar olan herhangi bir durumu dogrular nitelikte olan klasik bir degeri nicemler OrneklerUyumlu Salingac Harmonik Osilator Eski kuantum kuramindaki en basit sistem uyumlu harmonic salingacdir Bunun Hamiltonyan i H p22m mw2q22 displaystyle H p 2 over 2m m omega 2 q 2 over 2 Bu denklemde H displaystyle H nin gruplarinin seviyesi yorungelerdir ve buradaki kuantum nicem durumu faz boslugunda bir yorunge tarafindan kapatilmis alandir ve bu alan bir tam sayidir Planck kuralina gore enerji nicemlenir E nℏw displaystyle E n hbar omega Bu sonuc onceden de oldukca iyi bilinmekteydi ve eski kuantum sartini formulize etmek icin kullanilmistir Bu sonuc kuantum mekaniginin yardimlariyla bulunan 12ℏw displaystyle frac 1 2 hbar omega ile farklilik gosterir Bu sabit eski kuantum kuraminin turetimlerinde turev almalarinda yok sayilirdir ve sabitin degeri bu kullanilarak belirlenemez Nicemlenmis bir salingacin osilatorun isisal termal ozellikleri Boltzmann agirligi ile baglanmis oldugunu varsaydigimiz her bir ayrik durgunun emerjilerinin ortalamasi alinarak bulunabilir U nℏwne bnℏw ne bnℏw ℏwe bℏw1 e bℏw whereb 1kT displaystyle U sum n hbar omega ne beta n hbar omega over sum n e beta n hbar omega hbar omega e beta hbar omega over 1 e beta hbar omega rm where beta frac 1 kT Bu denklemde kT displaystyle kT Boltzmann sabitinin mutlak sicaklikla carpimidir Buradaki sicaklik daha cok enerjinin dogal birimlerinde olculur Termodinamikte Isi Devinimde b displaystyle beta miktari sicakliktan daha temeldir cunku b displaystyle beta enerjiyle iliskili termodinamik Isi Devinim potansiyelidir gerilimidir Bu ifadeden anlasilacagi uzere kolaylikla gorulur ki buyuk b displaystyle beta degerlerinde cok dusuk sicakliklar icin olmak kaydiyla Harmonik osilatordeki Uyumlu Salingac ortalama enerji suratle sifira yaklasir ve bu durum ussel eksponent olarak hizlidir Bunun arkasinda yatan sebep ise kT nin bir T sicakliginda rastgele secilmis olan bir hareketteki kendine ozgu enerji olmasidir Ayrica kT displaystyle kT ℏw displaystyle hbar omega dan kucuk oldugunda ortamda salingaca verilecek bir kuantum enerjisi bile yeterli derecede olmaz Dolayisiyla salingac taban durumunda kalmaya devam eder Bunun anlami cok dusuk sicakliklarda betaya gore enerjideki degisim veya esit bir bicimde sicakliga gore enerjideki degisim ussel olarak kucuktur Sicakliga gore enerjideki degisim oz isidir Dolayisiyla oz isi dusuk sicakliklarda ussel olarak kucuktur ve sifira dogru asagidaki gibi gitmektedir exp ℏw kT displaystyle exp hbar omega kT dd Kucuk b displaystyle beta degerlerinde ve yuksek sicakliklarda ortalama enerji U 1b kT displaystyle frac 1 beta kT ye esittir Bu klasik termodinamigin esbolum kuramini tekrar gundeme getirmektedir Bu kuram Bir T sicakliginda her uyumlu salingacin kT enerjisi vardir ve bu enerji ortalamadadir der Bunun anlami klasik mekanik de herhangi bir salingacin oz isisi sabittir ve k ya esittir Yaylarla baglanmis bir atom toplami icin makul bir kati modeli olmak kaydiyla toplam oz isi toplam salingac sayisinin k ile carpimina esittir Ornek vericek olursak toplmada her atom icin uc salingacin oldugu bir yerde 3 boyutta bagimsiz salingaclar icin 3 olasi yon vardir Dolayisiyla klasik bir katinin oz isisi her zaman atom basina 3k dir veya Kimya birimleriyle aciklayacak olursak bir mol atom icin 3R dir Oda sicakliginda tek atomlu katilar yaklasik olarak atom basina 3k ile ayni oz isiya sahiptirler Fakat bu durum dusuk sicakliklarda gecerli degildir Daha dusuk sicakliklarda oz isi da daha kucuktur ve sifira dogru gitmektedir Bu butun materyal sistemleri icin dogrudur ve bu gozlem termodinamigin ucuncu yasasi olarak bilinir Klasik mekanik ucuncu yasayi aciklayamaz cunku klasik mekanikde oz isi sicakliktan bagimsizdir Klasik mekanik ve soguk malzemelerin oz isisi arasindaki bu celiskiyi 19 yuzyilda James Clerk Maxwell dikkate almistir 1906 da Albert Einstein bu problemi atomic hareketin nicemlenmis oldugunu ileri surerek yeniden cozmustur Bu kuantum kuraminin mekanik sistemlere uyarlanmis ilk uygulamasaydi Cok kisa bir sure sonra Peter Debye katilarin oz isilari hakkinda ortaya nicel bir kuram sunmustur Tek Boyutlu Potansiyel Gerilim U 0 Tek boyutlu problemlerin oldukca basittir Herhangi bir E displaystyle E enerjisinde p displaystyle p momentum devinim degeri asagidaki formulle bulunabilir 2m E V q p displaystyle sqrt 2m E V q p Momentumun Devinimin ortadan kayboldugu yerde klasik donum noktalari arasindaki butun q displaystyle q degerleri tumlenmistir Uzunlugu L displaystyle L kadar olan bir kutudaki parcacik icin bu integral en kolay halindedir ve formul su sekilde olur 2 0Lpdq nh displaystyle 2 int 0 L p dq nh Bu formul bize momentumu da vermektedir p nh2L displaystyle p nh over 2L Ve son olarak enerji seviyeleri En p22m n2h28mL2 displaystyle E n p 2 over 2m n 2 h 2 over 8mL 2 Tek Boyutlu Potansiyel Gerilim U Fx Eski kuantum kurami ile kolayca cozulebilen bir baska husus ise pozitif arti yari yoldaki dogrusal gerilimdir lineer potansiyel Buradaki olay girilemez bir duvara sabit ve sinirli bir F displaystyle F kuvvetli parcacigi baglamaktir Bu husus kuantum mekaniksel islemlerde cok daha zordur Ayrica diger orneklerin aksine burada kismen klasik cevaplar kesin olmayan yaklasik cevaplardir ve buyuk kuantum numaralarinda daha kesin olmaktadir 2 0EF2m E Fx dx nh displaystyle 2 int 0 frac E F sqrt 2m E Fx dx nh dolayisiyla kuantum durumu su sekilde olur 432mE3 2F nh displaystyle 4 over 3 sqrt 2m E 3 2 over F nh Bu denklem enerji seviyelerini aciklar En 3nhF42m 2 3 displaystyle E n left 3nhF over 4 sqrt 2m right 2 3 F mg ozel durumunda ise parcacik dunyanin yercekimi potansiyeli tarafindan sinirlandirilmistir Ayrica burada duvar olarak yeryuzu kastedilmektedir Doner Rotator Bir baska basit sistem ise donerdir Bir doner iki boyutta kutlesiz R uzunlugundaki sabit bir cubugun ucunda M kadar kutle ihtiva ettiginde bu donerin Lagrangian i L MR228 2 displaystyle L MR 2 over 2 dot theta 2 olur ve bu denklem polar kutuplu 8 displaystyle theta acisi ile eslenik olan acisal momentumu J displaystyle J devinimi aciklar Buna gore acisal momentum formulu J MR28 displaystyle scriptstyle J MR 2 dot theta olarak tanimlanir Eski kuantum durumu acisal momentumun 8 displaystyle theta acisinin periyodu ile carpilmasini gerektirmektedir Burada 8 displaystyle theta acisinin periyodu Planck sabitinin birden fazla tam sayisidir 2pJ nh displaystyle 2 pi J nh Bohr modelinde bu kisitlama dairesel yorungelerde bulunan enerji seviyelerini aciklamayi zorlamaktadir 3 boyutta sabit bir doner 8 displaystyle theta ve ϕ displaystyle phi acilari ile tanimlanabilir Burada 8 displaystyle theta acisi rastgele secilen bir z eksenindeki egime karsilik gelirken ϕ displaystyle phi acisi ise x y ekseninde bulunan doner acisina karsilik gelmektedir Buna gore kinetik devimsel enerjinin Lagrangian i L MR228 2 MR22 sin 8 ϕ 2 displaystyle L MR 2 over 2 dot theta 2 MR 2 over 2 sin theta dot phi 2 Bu durumda eslenik momentum p8 8 displaystyle scriptstyle p theta dot theta ve pϕ sin 8 2ϕ displaystyle scriptstyle p phi sin theta 2 dot phi olur ϕ displaystyle scriptstyle phi icin hareket denklemi belirsizdir ve pϕ displaystyle scriptstyle p phi bir sabittir pϕ lϕ displaystyle p phi l phi olur ki bu da z bileskesinin acisal momentumudur Kuantum durumu lϕ displaystyle scriptstyle l phi sabitinin integraline tumlevine dayanir cunku ϕ displaystyle scriptstyle phi acisi 0 displaystyle 0 ile 2p displaystyle 2 pi arasinda cesitlilik gosterir lϕ mℏ displaystyle l phi m hbar Burada m manyetik miknatisal duygunluk kuantum sayisi olarak anilir cunku acisal momentumun z bileskesi z ekseni boyunca donerin manyetik momentumudur Bu esitlik donerin sonunda bulunan parcacigin yuklenmis durumlarda gecerlidir 3 boyutlu doner bir eksen etrafinda dondugu icin toplam acisal momentum 2 boyutlu donerde oldugu gibi sinirlandirilmalidir Iki kuantum durumunda toplam acisal momentumu ve l m displaystyle l m gibi katsayi olan z bileskesinin acisal momentumunu kisitlamaktadir Bu durum modern gunumuz kuantum mekaniginde yeniden turetilmistir Fakat eski kuantum kurami doneminde bu durum bir paradoks ozceliski olusmasina yol acmistir Bu paradoks Rastgele secilmis bir z eksenine gore acisal momentumun yonu nasil kuantize nicemleme edilebilir dir Gorulen o ki bu durum uzayda boslukda bir yon cikartmaktadir Bu fenomen bir eksen etrafinda bulunan acisal momentumun kuantize edilmesi bosluk kuantizasyonu olarak adlandirilmistir cunku bu durum rotasyonel donussel degismezlik ile uyumsuz gorunmustur Modern kuantum mekaniginde acisal momentum ayni sekilde kuantize edilir fakat herhangi bir yondeki acisal momentumun ayrik durumlari diger yonlerdeki durumlarin kuantum super pozisyonudur ustdusumudur Dolayisiyla kuantizasyonun islem sureci tercih edilen bir eksen cikarmamaktadir Bu nedenle bosluk kuantizasyonu ismi gozden dusmus onun yerine bu fenomen acisal momentum kuantizasyonu olarak anilmaya baslamistir Hidrojen Atomu Hidrojen atomunun acisal bolumu sadece bir donerden rotator ibarettir ve bu bize kuantum numaralari olan l displaystyle l ve m displaystyle m yi verir Arda kalan tek degisken ise radial koordinatdir yaricapsal konsayi Toplam acisal momentum devinimi L displaystyle L kadar olan sabit bir deger icin ki bu klasik bir Kepler problemidir kutlenin ve enerjinin birimi iki sabiti sogurmak absorbe etmek icin tekrar tanimlanmisti Hamiltonyan su sekilde olur H p22 l22r2 1r displaystyle H p 2 over 2 l 2 over 2r 2 1 over r Enerjiyi sabit bir degere oturtmak ve p displaystyle p radial momentumu yaricapsal devinim cozmek icin kuantum nicem durumu integrali tumlevi asagidaki gibi olur 2 2E l2r2 2r dr kh displaystyle 2 int sqrt 2E l 2 over r 2 2 over r dr kh Bu yalin bir denklemdir ve bize l displaystyle l ile bagintili enerjiyi tanimlayan k displaystyle k kuantum numarasini vermektedir Bu durumda enerjinin formulu asagidaki gibi olmaktadir E 12 k l 2 displaystyle E 1 over 2 k l 2 Bu formul asil kuantum sayisi n displaystyle n e karsilik gelen k displaystyle k ve l displaystyle l nin toplamlarina dayanmaktadir k displaystyle k pozitif arti oldugu icin herhangi bir n displaystyle n degeri icin l displaystyle l degeri n displaystyle n den buyuk olamaz Bu enerjiler Bohr modelinde yeniden tanimlanmaktadir Fakat bu tanimlamada yuksek degerlerde bazi belirsizliklere sahip olan kuantum mekaniksel carpanlar haric tutulmustur Kismen klasik olan hidrojen atomu Sommerfeld modeli olarak adlandirilir ve ayrik egimlerde bu atomun yorungeleri farkli olculerde ve eliptik olur Sommerfeld modelinin tahminine gore bir atomun manyetik momentu ancak ayrik degerler alacak bir eksen boyunca olculebilir Bunun isiginda yapilan olcumler sonucu elde edilen bir sonuc rotasyonal degismezlik ile celiskili gorunmustur ama bu sonuc Stern Gerlach deneyi ile onaylanmistir Bohr Sommerfeld kurami kuantum mekanigin gelisiminin bir parcasidir ve atomik enerji seviyelerinin manyetik alanlar tarafindan yarilma ihtimalini tanimlayabilmektedir Relativistik Goreli Yorunge Arnold Sommerfeld atomik enerji seviyelerinin relativistik goreli cozumlerini tureten kisidir Bu turetmeye elektrik potansiyeldeki gerilim enerji icin relativistik denklemle baslamak gerekmektedir W m0c2 11 v2c2 1 kZe2r displaystyle W m mathrm 0 c 2 left frac 1 sqrt 1 frac v 2 c 2 1 right k frac Ze 2 r u 1r displaystyle u frac 1 r degisimini yaptigimizda 11 v2c2 1 Wm0c2 kZe2m0c2u displaystyle frac 1 sqrt 1 frac v 2 c 2 1 frac W m mathrm 0 c 2 k frac Ze 2 m mathrm 0 c 2 u Momentum icin pr mr displaystyle p mathrm r m dot r pf mr2f displaystyle p mathrm varphi mr 2 dot varphi esitligini elde ederiz ve birbirlerine orani prpf dudf displaystyle frac p mathrm r p mathrm varphi frac du d varphi olur Bu durumda hareket denklemi bkz Binet Denklemi d2udf2 1 k2Z2e4c2pf2 u m0kZe2pf2 1 Wm0c2 w02u K displaystyle frac d 2 u d varphi 2 left 1 k 2 frac Z 2 e 4 c 2 p mathrm varphi 2 right u frac m mathrm 0 kZe 2 p mathrm varphi 2 left 1 frac W m mathrm 0 c 2 right omega mathrm 0 2 u K cozumuyle u 1r K Acos w0f displaystyle u frac 1 r K A cos omega mathrm 0 varphi Enberi noktasinin periapsis acisal kaymasi devir basina su sekilde olur fs 2p 1w0 1 4p3k2Z2e4c2nf2h2 displaystyle varphi mathrm s 2 pi left frac 1 omega mathrm 0 1 right approx 4 pi 3 k 2 frac Z 2 e 4 c 2 n mathrm varphi 2 h 2 Kuantum durumu ile ele aldigimizda pfdf 2ppf nfh displaystyle oint p mathrm varphi d varphi 2 pi p mathrm varphi n mathrm varphi h ve prdr pf 1rdrdf 2df nrh displaystyle oint p mathrm r dr p mathrm varphi oint left frac 1 r frac dr d varphi right 2 d varphi n mathrm r h Buradan enerjileri tanimlayabiliriz Wm0c2 1 a2Z2 nr nf2 a2Z2 2 1 2 1 displaystyle frac W m mathrm 0 c 2 left 1 frac alpha 2 Z 2 n mathrm r sqrt n mathrm varphi 2 alpha 2 Z 2 2 right 1 2 1 Bu denklemde a displaystyle alpha ince yapi sabitine denk gelmektedir Bu cozum Dirac denklemiyle aynidir De Broglie Dalgalari1905 yilinda Einstein kisa dalga boylari icin kutu icinde kuantize olmus elektromanyetik akimmiknatisal olan osilatorlerinin salingac entropisinin daginti bir gazin noktasal parcaciklarinin entropisine esit oldugunu belirtti Noktasal parcaciklarin sayisi kuantalarin nicem paketlerinin sayisina esittir Einstein bu kuantaya erisilebilir nesneler isik parcacikalri gibi davranabilecegine kanaat getirdi ve foton isincik olarak adlandirdi bkz sayfa 139 140 Einstein in bu kuramsal argumani termodinamige isidevinimsel durum numaralarini saymaya dayaniyordu ve tam olarak ikna edici degildi Sonuc olarak Einstein da isigi hem parcacik hem de dalga olarak atfetmistir Daha acikca w displaystyle omega frekansli tekrarsiklik bir duragan elektromanyetik dalga kuantize seviyesi E nℏw displaystyle E n hbar omega ile her biri ℏw displaystyle scriptstyle hbar omega enerjili n sayida fotondan olusmustur Einstein fotonlarin dalgalarla olan iliskisini aciklayamamistir Fotonlar enerji gibi momentumada sahiptir ve momentum k displaystyle k elektromanyetik dalganin dalga sayisi olmak uzere ℏk displaystyle scriptstyle hbar k ya esit olmak zorundadir Bu goreceliligin geregidir cunku momentum ve enerji frekans ve dalga sayisi olmak uzere yoney olusturur 1924 yilinda Doktora adayi Louis de Broglie kuantum durumuna yeni bir yontem onerdi Elektronlari da fotonlar gibi iliskilere uyacak dalga seklinde tanimlayabilmistir p ℏk displaystyle p hbar k veya dalga boyu l displaystyle lambda cinsinden yazildiginda p hl displaystyle p h over lambda Louis de Broglie sonrasinda kuantum kosullarini soyle belirtmistir pdx ℏ kdx 2pℏn displaystyle int p dx hbar int k dx 2 pi hbar n Klasik yorungeyi takip eden dalga icin faz degisimlerini sayar ve bu 2p displaystyle 2 pi nin tam kati olmasini gerektirir Dalga boyu cinsinden klasik yorungeyi takip eden dalga boylarinin sayisi tam sayi olmak zorundadir Bu yapici girisimin sartidir ve kuantize yorungelerin sebebini aciklar Madde dalgalari sadece ayrik frekans ve enerjilerde duragan dalga olusturur Ornegin bir kutuda hapsedilmis bir parcacik icin bir duragan dalga duvarlarinin arasindaki mesafenin iki kati dalga boyunun tam sayi kati olmak zorundadir Bu sart asagidaki denklemle ifade edilir nl 2L displaystyle n lambda 2L Dolayisiyla kuantize momentum p nh2L displaystyle p frac nh 2L olur Eski kuantum enerji duzeylerini yeniden olusturur Bu geliime Einstein tarafindan daha matematiksel bir formda verilmistir Einstein dalgalar icin faz fonskiyonunu islevini soyle belirtir Hamilton dahi dalga mekaniginin kisa dalga boyu limiti siniri icin tanimladigi bir denklemi mekanik bir sistemde Hamilton Jacobi denklemlerinin cozumuyle tanimlamaktadir Bu fikirler Schrodinger denkleminin kesfine yol acmistir Kramers Gecis Matrisi Dizeyi Eski kuantum kurami sadece periyodik olan hareket aci degiskenlerine ayrilmis ozel mekanik sistemler icin formule edilmistir Isinim salinimi veya emilimiyle ilgilenmemisti Yine de Hendrik Kramers emilim ve salinimin nasil hesaplanmasi gerektigini sezgisel olarak tanimlamistir Kramer kuantum sisteminin yorungelerinin Fourier analizlerinin yeni harmoniklerin yorunge frekanslarini katlari seklinde ayristirilmasiyla analiz edilmesini onermistir Xn t k eikwtXn k displaystyle X n t sum k infty infty e ik omega t X n k Indeks dizin n displaystyle n yorunde kuantum numarasini tanimlar o da Sommerfeld modelinde n l m displaystyle n l m olacaktir Frekans w displaystyle omega k displaystyle k Fourier modunun bir indeksi olmak uzere 2p Tn displaystyle scriptstyle 2 pi T n yeni yorungenin acisal frekansidir Bohr klasik hareketin k th harmoniginin n displaystyle n duzeyinden n k displaystyle n k duzeyine gecisine karsilik geldigini onerir Kramers durumlar arasi gecisi isinimin klasik salinimina benzerligini ki bu yorunge frekansinin katlarindaki frekanslarda gerceklesir onermistir Isinim saliniminin orani Xk 2 displaystyle X k 2 ile dogru orantilidir Bu klasik mekanikde de boyledir Tanim yaklasiktir cunku Fourier bilesenleri duzeyler arasi enerji bosluklari ile tam olarak uyusmayan frekanslara sahip degildir Bu dusunce matris mekaniginin gelismesine sebep olmustur Eski Kuantum Kuraminin SinirlariEski kuantum kurami bazi sinirlamalara sahiptir Eski kuantum kurami spektral tayfsal cizgilerin siddetlerini hesaplayamamistir Eski kuantum kurami mustesna Zeeman tesirini aciklayamamistir Burada elektron spinleri goz ardi edilemez Eski kuantum kurami kaotik sistemleri kuantize edemez Yani hareketli sistemlerin yorungeleri ne yakindir ne periyodiktir ne de analitik form olusturabilir Bu unlu kutle cekimsel 3 parca problemine klasik kaotik benzeri olan 2 elektronlu atom kadar kolay sistemler icin dahi sorular ortya cikarir Fakat bu Zeeman etkisi ile tek elektrondan fazla elektronlari bulunan atomlari tanimlamak icin kullanilabilir Sonradan eski kuantum kurami aslinda kaotik kuantum mekaniginin kismen klasik varsayimlari oldugunu one surmustur fakat bu sinirlar hala arastirilmaktadir TarihiEski kuantum kurami Max Planck tarafindan isigin salinimi ve sogurulmasi uzerine ortaya cikarilmis ve Albert Einstein in katilarin oz isisi uzerine calismasindan sonra dikkate alinmistir Einstein daha sonradan Debye atomlarin hareketinin kuantum prensiplerine uygulamis ve oz isi anormalliklerini aciklamistir 1913 yilinda Bohr benzerlik prensibini tanimlamis ve cizgi tayfini aciklayan hidrojen atomu modelini formule etmek icin kullanmistir Birkac yil icerisinde Arnold Sommerfeld gelisiguzel tumlevlenebilir sistemlerin Einstein ve Lorentz tarafindan tanimlanmis kuantum sayilarinin yalitilmis degismezliginin prensiplerini kullanarak genisletmistir Sommerfeld modeli modern kuantum mekanigine Bohr unkinden daha yakindir 1910 ve 1920 li yillar boyunca oldugu gibi bircok problem karisik sonuclarla eski kuantum kurami kullanilarak cozumlenmeye calisilmistir Molekuler donusler ve titresimler tayfi anlasilmis ve elektron spinleri kesfedilmistir Bu yarim katlarda bulunan kuantum sayilari karmasasina yol acmistir Max Planck sifir nokta enerjisini tanimladi ve Arnold Sommerfeld relativistik hidrojen atomunu kismen klasik olarak kuantize etmistir Hendrik Kramers Stark etkisini acikladi Bose Einstein da fotonlarin dogru kuantum istatistiklerini verdi Kramers kuantum durumlarin hareketin Fourier bileskesi cinsinden olanlarinin arasindaki gecis ihtimallerini hesaplamaya yonelik bir yonergede bulunmustur Bu fikir Werner Heisenberg in isbirligi ile kismen klasik matrise kadar genisletilmistir Unutulmamalidir ki kismen klasik matris atomik gecis ihtimallerinin tanimina benzer Heisenberg bu matris mekanigini yaratarak butun kuantum kuramini bu gecis matrisleri cinsinden yeniden formulize etmistir 1924 yilinda Louis de Broglie maddenin dalga kuramini ortaya sunmustur Bu kuram kisa sure sonra Albert Einstein tarafindan madde dalgalari icin kismen klasik denklemler kullanilarak genisletilmistir 1926 da Erwin Schrodinger tamamiyla dogru olan bir kuantum mekaniksel dalga denklemi bulmustur Bu bulus eski kuantum kuraminin basarilarini belirsizlik ve tutarsizlik olmaksizin yeniden sunmustur Schrodinger in dalga mekanigi Schrodinger ve diger bilim insanlari iki yontemin ayni deneysel tesaduflere sahip olacagini kanitlayana kadar matris mekaniginden ayri olarak gelismistir Daha sonra Paul Dirac 1926 yilinda iki yonteminde daha kapsamli bir yontem olan donusum kurami ile elde edilebilecegini yazmistir Kaynakca ter Haar D 1967 The Old Quantum Theory Pergamon Press ss 206 ISBN 0 08 012101 2 Sommerfeld Arnold 1919 Atombau und Spektrallinien Braunschweig Friedrich Vieweg und Sohn ISBN 3 87144 484 7 Arnold Sommerfeld 1921 Atombau und Spektrallinien Braunschweig 1 Ya I Granovski 2004 Sommerfeld formula and Dirac s theory PDF Physics Uspekhi 47 5 ss 523 524 Bibcode 2004PhyU 47 523G doi 10 1070 PU2004v047n05ABEH001885 Einstein Albert 1905 PDF Annalen der Physik 17 6 ss 132 148 Bibcode 1905AnP 322 132E doi 10 1002 andp 19053220607 9 Temmuz 2011 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 18 Subat 2008 Chaddha G S 2006 Quantum Mechanics New Dehli New Age international ss 8 9 ISBN 81 224 1465 6 23 Temmuz 2014 tarihinde kaynagindan Erisim tarihi 11 Haziran 2014 E A Solov ev E A 2011 Classical approach in atomic physics European Physical Journal D 65 3 ss 331 351 arXiv 1003 4387 2 Bibcode 2011EPJD 65 331S doi 10 1140 epjd e2011 20261 6 L D Landau 1977 Quantum Mechanics Non Relativistic Theory 3rd Vol 3 Pergamon Press ISBN 978 0 08 020940 1 Konuyla ilgili yayinlarThewlis J Ed 1962 Encyclopaedic Dictionary of Physics Pais Abraham 1982 Max Born s Statistical Interpretation of Quantum Mechanics PDF Science 218 4578 ss 1193 8 Bibcode 1982Sci 218 1193P doi 10 1126 science 218 4578 1193 PMID 17802457 2 Agustos 2021 tarihinde kaynagindan PDF Erisim tarihi 11 Haziran 2014 Address to annual meeting of the Optical Society of America October 21 1982 Tucson AZ Retrieved 2013 09 08
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans


































