Euler spirali, eğimi eğrinin uzunluğuyla doğrusal olarak degişen bir eğridir. Euler spiralleri yaygın olarak spiros, clothoids veya Cornu spiralleri olarak da adlandırılır. Euler spirallerinin kırınım hesaplamalarında uygulamaları vardır. Genellikle demiryolu ve karayolu mühendisliklerinde teğet eğrisi ve dairesel eğri arasındaki geometriyi bağdaştırmaya ve aktarmaya yarayan geçiş eğrisi olarak kullanılır. Teğet eğrisi ve dairesel eğri arasındaki geçiş eğrisinin eğimindeki lineer değişim prensibi Euler spiralinin geometrisini belirler:
- Eğimi teğetin düzgün kesitinden başlayarak lineer olarak eğri boyunca artar.
- Euler spiralinin dairesel eğriyle karşılaştığı yerde eğimi dairesel eğrinin eğimine eşit olur.

Uygulamaları
Geçiş eğrisi
Dairesel yörüngede hareket eden bir nesne merkezcil ivmeye maruz kalır. Bir araç düz bir yörüngeden dairesel bir yörüngeye yaklaşırken aniden teğet noktasında başlayan merkezcil ivmeyi hissedecektir. İlk demiryollarında trenlerin düşük hızla hareket etmesinden ve yörüngelerin geniş yarıçaplı eğrilerden oluşmasından dolayı şimdiki yanal kuvvet uygulaması bir sorun oluşturmamaktaydı. Demiryolu taşıtlarının hızı günden güne arttıkça konforun gerekli olduğu ortaya çıktı. Bu yüzden de merkezcil ivme yolculuk mesafesiyle doğrusal olarak artmaktadır. Konforun sağlanması için eğimi alınan mesafeyle doğrusal olarak artan bir eğri çözüm olarak bulundu. Bu geometrik ifade Euler spiralidir. Leonhard Euler’in geometri çözümünden habersiz olarak Rankine Euler spiralinin dairesel bir eğriye yakınsayan bir parabol üzerindeki küçük açısal değişiklikler üzerinden yapılan bir yaklaşımı olan kübik eğriden () bahsetmiştir. Marie Alfred Cornu ve daha sonra başka inşaat mühendisleri de Euler spiralinin hesaplamalarını birbirlerinden bağımsız olarak çözmüşlerdir. Günümüzde Euler spiralleri yaygın olarak demiryolu ve karayolu mühendisliklerinde teğet eğrisi ve yatay dairesel eğri arasında geçişi ve konforu sağlamak için kullanılır.
Optik
Cornu spirali kırınım desenini betimlemek için kullanılır.
Formülasyon
Semboller
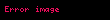 | Eğim yarıçapı |
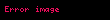 | Spiralin sonundaki dairesel eğimin yarıçapı |
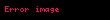 | Başlangıç noktasından spiral üzerindeki herhangi bir noktaya kadar uzanan eğrinin açısı. |
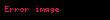 | Bütün spiralin açısı |
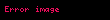 | Başlangıç noktasından başlanarak spiral boyunca katledilen uzunluk |
 | Spiral eğrisinin uzunluğu |
Çıkarımlar

Sağ taraftaki grafik Euler spiralinin negatif x ekseni boyunca uzanmış düz bir çizgiyle bir çember arasındaki geçiş eğrisi olarak kullanıldıgını göstermektedir. Spiral pozitif x ekseni üzerindeki orijinden başlayarak gitgide saat yönünün tersinde dönerek çembere değer. Spiral ilk kadrandaki çift sonlu Euler spiralinin yukarısındaki küçük bir kısımdır.
- Eğim tanımından yola çıkılarak,
- Aşağıdaki şekilde yazarsak,
- ya da ::
- Böylece
olur.
- Eğer
olduğunu kabul edersek,
.
- Böylece ::
elde ederiz.
Fresnel integral açılımı
A'nın olduğu yani Euler eğrisinin normalize edilebilir olduğu durumlarda kartezyen koordinatlar Fresnel integrali (ya da Euler integrali) ile aşağıdaki gibi belirlenir:
Kosinüs açılımına göre C(L)'yi :
Sinüs açılımına göreyse S(L)'yi:
bu şekillerde elde ederiz.
Normalize etme ve sonuç
Verilen Euler eğrisi için:
ya da
geçerliyse,
where 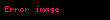
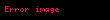
Euler spiralinin (x,y) cinsinden çözümünün elde edilme süreci şu şekilde belirlenebilir:
- Orijinal Euler spiralinin uzunluğu L a ile çarpılarak normalize edilmiş Euler spiralinin uzunluğu Le eşlenir;
- Fresnel integralinden (x',y') bulunur; ve
- (x',y') 1/a oranında arttırılarak (x,y)'ye eşlenir. (1/a > 1)
Normalizasyon süresince,
Normalizasyon genel olarak Lı 1'den küçük bir değere götürür.
Örnekleme
Verilen:
değerleri için,
olur.
Euler spiralini √60,000 küçültürsek, yani normalize Euler spiralinin 100√6 olması durumunda:
ve
Yukarıda iki açı 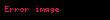
Normalize Euler spiralinin diğer özellikleri
Normalize Euler spirali şu şekilde ifade edilir:
ve normalize Euler spiralinin bazı özellikleri şunlardır:
ve
Euler spiral üretmek için gereken kodlar
Aşağıdaki Sage koduyla yukarıdaki ikinci grafik elde edilebilir. İlk 4 satır Euler spirali bileşenlerini ifade eder. fresnel fonksiyonlarının yerine iki Taylor seri açılımı adapte edilmiştir. Geriye kalan kodlarsa sırayla teğet ve daireyi ifade eder.
var('L') p = integral(taylor(cos(L^2), L, 0, 12), L) q = integral(taylor(sin(L^2), L, 0, 12), L) r1 = parametric_plot([p, q], (L, 0, 1), color = 'red') r2 = line([(-1.0, 0), (0,0)], rgbcolor = 'blue') x1 = p.subs(L = 1) y1 = q.subs(L = 1) R = 0.5 x2 = x1 - R*sin(1.0) y2 = y1 + R*cos(1.0) r3 = circle((x2, y2), R, rgbcolor = 'green') show(r1 + r2 + r3, aspect_ratio = 1, axes=false) Aşağıdaki Mathematica kodu da Euler spiralinin bileşenleri içindir; wolframalpha.com'da sorunsuz bir şekilde çalışır.
ParametricPlot[ {FresnelC[Sqrt[2/\[Pi]] t]/Sqrt[2/\[Pi]], FresnelS[Sqrt[2/\[Pi]] t]/Sqrt[2/\[Pi]]}, {t, -10, 10}] Kaynakça
Konuyla ilgili okumalar
- Kellogg, Norman Benjamin (1907). The Transition Curve or Curve of Adjustment. 3rd. New York: McGraw.
- R. Nave, The Cornu spiral, Hyperphysics (2002) (Uses πt²/2 instead of t².)
- Milton Abramowitz and Irene A. Stegun, eds. with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 7)
- . 10 Ekim 2006 tarihinde kaynağından arşivlendi. Erişim tarihi: 12 Kasım 2010.
Dış bağlantılar
- Eric W. Weisstein, Cornu Spiral (MathWorld)
- Euler's spiral at 2-D Mathematical Curves
- Interactive example with JSXGraph
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Euler spirali egimi egrinin uzunluguyla dogrusal olarak degisen bir egridir Euler spiralleri yaygin olarak spiros clothoids veya Cornu spiralleri olarak da adlandirilir Euler spirallerinin kirinim hesaplamalarinda uygulamalari vardir Genellikle demiryolu ve karayolu muhendisliklerinde teget egrisi ve dairesel egri arasindaki geometriyi bagdastirmaya ve aktarmaya yarayan gecis egrisi olarak kullanilir Teget egrisi ve dairesel egri arasindaki gecis egrisinin egimindeki lineer degisim prensibi Euler spiralinin geometrisini belirler Egimi tegetin duzgun kesitinden baslayarak lineer olarak egri boyunca artar Euler spiralinin dairesel egriyle karsilastigi yerde egimi dairesel egrinin egimine esit olur Cift sonlu Euler spirali UygulamalariGecis egrisi Dairesel yorungede hareket eden bir nesne merkezcil ivmeye maruz kalir Bir arac duz bir yorungeden dairesel bir yorungeye yaklasirken aniden teget noktasinda baslayan merkezcil ivmeyi hissedecektir Ilk demiryollarinda trenlerin dusuk hizla hareket etmesinden ve yorungelerin genis yaricapli egrilerden olusmasindan dolayi simdiki yanal kuvvet uygulamasi bir sorun olusturmamaktaydi Demiryolu tasitlarinin hizi gunden gune arttikca konforun gerekli oldugu ortaya cikti Bu yuzden de merkezcil ivme yolculuk mesafesiyle dogrusal olarak artmaktadir Konforun saglanmasi icin egimi alinan mesafeyle dogrusal olarak artan bir egri cozum olarak bulundu Bu geometrik ifade Euler spiralidir Leonhard Euler in geometri cozumunden habersiz olarak Rankine Euler spiralinin dairesel bir egriye yakinsayan bir parabol uzerindeki kucuk acisal degisiklikler uzerinden yapilan bir yaklasimi olan kubik egriden bahsetmistir Marie Alfred Cornu ve daha sonra baska insaat muhendisleri de Euler spiralinin hesaplamalarini birbirlerinden bagimsiz olarak cozmuslerdir Gunumuzde Euler spiralleri yaygin olarak demiryolu ve karayolu muhendisliklerinde teget egrisi ve yatay dairesel egri arasinda gecisi ve konforu saglamak icin kullanilir Optik Cornu spirali kirinim desenini betimlemek icin kullanilir FormulasyonSemboller R displaystyle R Egim yaricapiRc displaystyle R c Spiralin sonundaki dairesel egimin yaricapi8 displaystyle theta Baslangic noktasindan spiral uzerindeki herhangi bir noktaya kadar uzanan egrinin acisi 8s displaystyle theta s Butun spiralin acisiL s displaystyle L s Baslangic noktasindan baslanarak spiral boyunca katledilen uzunlukLs so displaystyle L s s o Spiral egrisinin uzunluguCikarimlar Sag taraftaki grafik Euler spiralinin negatif x ekseni boyunca uzanmis duz bir cizgiyle bir cember arasindaki gecis egrisi olarak kullanildigini gostermektedir Spiral pozitif x ekseni uzerindeki orijinden baslayarak gitgide saat yonunun tersinde donerek cembere deger Spiral ilk kadrandaki cift sonlu Euler spiralinin yukarisindaki kucuk bir kisimdir Egim tanimindan yola cikilarak 1R d8dL L displaystyle frac 1 R frac d theta dL propto L dd RL constant RcLs displaystyle RL text constant R c L s d8dL LRcLs displaystyle frac d theta dL frac L R c L s dd Asagidaki sekilde yazarsak d8dL 2a2L displaystyle frac d theta dL 2a 2 L dd 2a2 1RcLs displaystyle 2a 2 frac 1 R c L s dd ya da a 12RcLs displaystyle a frac 1 sqrt 2R c L s Boylece8 aL 2 displaystyle theta aL 2 olur dd x 0Lcos 8ds 0Lcos as 2 ds displaystyle begin aligned x amp int 0 L cos theta ds amp int 0 L cos left as 2 right ds end aligned dd EgerL aL displaystyle L aL oldugunu kabul edersek dL dL a displaystyle dL frac dL a dd dd Boylece x 1a 0L cos s2ds displaystyle x frac 1 a int 0 L cos s 2 ds elde ederiz y 0Lsin 8ds 0Lsin as 2 ds 1a 0L sin s2ds displaystyle begin aligned y amp int 0 L sin theta ds amp int 0 L sin left as 2 right ds amp frac 1 a int 0 L sin s 2 ds end aligned dd Fresnel integral acilimi A nin oldugu yani Euler egrisinin normalize edilebilir oldugu durumlarda kartezyen koordinatlar Fresnel integrali ya da Euler integrali ile asagidaki gibi belirlenir C L 0Lcos s2ds displaystyle C L int 0 L cos s 2 ds S L 0Lsin s2ds displaystyle S L int 0 L sin s 2 ds Kosinus acilimina gore C L yi cos 8 1 822 844 866 displaystyle cos theta 1 frac theta 2 2 frac theta 4 4 frac theta 6 6 cdots C L 0Lcos s2ds displaystyle C L int 0 L cos s 2 ds 0L 1 s42 s84 s126 ds displaystyle int 0 L 1 frac s 4 2 frac s 8 4 frac s 12 6 cdots ds L L55 2 L99 4 L1313 6 displaystyle L frac L 5 5 times 2 frac L 9 9 times 4 frac L 13 13 times 6 cdots Sinus acilimina goreyse S L yi sin 8 8 833 855 877 displaystyle sin theta theta frac theta 3 3 frac theta 5 5 frac theta 7 7 cdots S L 0Lsin s2ds displaystyle S L int 0 L sin s 2 ds 0L s2 s63 s105 s147 ds displaystyle int 0 L s 2 frac s 6 3 frac s 10 5 frac s 14 7 cdots ds L33 L77 3 L1111 5 L1515 7 displaystyle frac L 3 3 frac L 7 7 times 3 frac L 11 11 times 5 frac L 15 15 times 7 cdots bu sekillerde elde ederiz Normalize etme ve sonuc Verilen Euler egrisi icin 2RL 2RcLs 1a2 displaystyle 2RL 2R c L s frac 1 a 2 ya da 1R LRcLs 2a2L displaystyle frac 1 R frac L R c L s 2a 2 L gecerliyse x 1a 0L cos s2ds displaystyle x frac 1 a int 0 L cos s 2 ds y 1a 0L sin s2ds displaystyle y frac 1 a int 0 L sin s 2 ds where L aL displaystyle L aL and a 12RcLs displaystyle a frac 1 sqrt 2R c L s Euler spiralinin x y cinsinden cozumunun elde edilme sureci su sekilde belirlenebilir Orijinal Euler spiralinin uzunlugu L a ile carpilarak normalize edilmis Euler spiralinin uzunlugu Le eslenir Fresnel integralinden x y bulunur ve x y 1 a oraninda arttirilarak x y ye eslenir 1 a gt 1 Normalizasyon suresince Rc Rc2RcLs Rc2Ls displaystyle begin aligned R c amp frac R c sqrt 2R c L s amp sqrt frac R c 2L s end aligned Ls Ls2RcLs Ls2Rc displaystyle begin aligned L s amp frac L s sqrt 2R c L s amp sqrt frac L s 2R c end aligned 2Rc Ls 2Rc2LsLs2Rc 22 1 displaystyle begin aligned 2R c L s amp 2 sqrt frac R c 2L s sqrt frac L s 2R c amp tfrac 2 2 amp 1 end aligned Normalizasyon genel olarak Li 1 den kucuk bir degere goturur Ornekleme Verilen Rc 300mLs 100m displaystyle begin aligned R c amp 300 mbox m L s amp 100 mbox m end aligned degerleri icin 8s Ls2Rc 1002 300 0 1667 radian displaystyle begin aligned theta s amp frac L s 2R c amp frac 100 2 times 300 amp 0 1667 mbox radian end aligned olur 2RcLs 60 000 displaystyle 2R c L s 60 000 Euler spiralini 60 000 kucultursek yani normalize Euler spiralinin 100 6 olmasi durumunda Rc 36mLs 16m displaystyle begin aligned R c tfrac 3 sqrt 6 mbox m L s tfrac 1 sqrt 6 mbox m end aligned 2Rc Ls 2 36 16 1 displaystyle begin aligned 2R c L s amp 2 times tfrac 3 sqrt 6 times tfrac 1 sqrt 6 amp 1 end aligned ve 8s Ls 2Rc 162 36 0 1667 radian displaystyle begin aligned theta s amp frac L s 2R c amp frac tfrac 1 sqrt 6 2 times tfrac 3 sqrt 6 amp 0 1667 mbox radian end aligned Yukarida iki aci 8s displaystyle theta s da ayni Bu orijinal ve normalize edilmis Euler spirallerinin benzer geometrilere sahip oldugunu gostermektedir Normalize egrinin konumu Fresnel integraliyle belirlenebilirken orijinal Euler spiralinin konumu ise denormalizasyonla elde edilir Normalize Euler spiralinin diger ozellikleri Normalize Euler spirali su sekilde ifade edilir x 0Lcos s2ds displaystyle x int 0 L cos s 2 ds dd y 0Lsin s2ds displaystyle y int 0 L sin s 2 ds dd ve normalize Euler spiralinin bazi ozellikleri sunlardir 2RcLs 1 displaystyle 2R c L s 1 8s Ls2Rc Ls2 displaystyle theta s frac L s 2R c L s 2 ve 8 8s L2Ls2 L2 displaystyle theta theta s cdot frac L 2 L s 2 L 2 1R d8dL 2L displaystyle frac 1 R frac d theta dL 2L Euler spiral uretmek icin gereken kodlarAsagidaki Sage koduyla yukaridaki ikinci grafik elde edilebilir Ilk 4 satir Euler spirali bilesenlerini ifade eder fresnel fonksiyonlarinin yerine iki Taylor seri acilimi adapte edilmistir Geriye kalan kodlarsa sirayla teget ve daireyi ifade eder var L p integral taylor cos L 2 L 0 12 L q integral taylor sin L 2 L 0 12 L r1 parametric plot p q L 0 1 color red r2 line 1 0 0 0 0 rgbcolor blue x1 p subs L 1 y1 q subs L 1 R 0 5 x2 x1 R sin 1 0 y2 y1 R cos 1 0 r3 circle x2 y2 R rgbcolor green show r1 r2 r3 aspect ratio 1 axes false Asagidaki Mathematica kodu da Euler spiralinin bilesenleri icindir wolframalpha com da sorunsuz bir sekilde calisir ParametricPlot FresnelC Sqrt 2 Pi t Sqrt 2 Pi FresnelS Sqrt 2 Pi t Sqrt 2 Pi t 10 10 Kaynakca Eugene Hecht 1998 Optics 3rd edition Addison Wesley s 491 ISBN 0201304252 Konuyla ilgili okumalarKellogg Norman Benjamin 1907 The Transition Curve or Curve of Adjustment 3rd New York McGraw R Nave The Cornu spiral Hyperphysics 2002 Uses pt 2 instead of t Milton Abramowitz and Irene A Stegun eds with Formulas Graphs and Mathematical Tables New York Dover 1972 See Chapter 7 10 Ekim 2006 tarihinde kaynagindan arsivlendi Erisim tarihi 12 Kasim 2010 Dis baglantilarEric W Weisstein Cornu Spiral MathWorld Euler s spiral at 2 D Mathematical Curves Interactive example with JSXGraph
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State