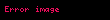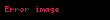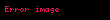Totient (kısaca φ, n) sayılar teorisinde, bir tam sayının o sayıdan daha küçük ve o sayı ile aralarında asal olan sayma sayı sayısını belirten fonksiyondur. Genellikle Euler Totient ya da Euler'in Totienti olarak adlandırılan Totient, İsviçreli matematikçi Leonhard Euler tarafından yaratılmıştır. Totient fonksiyonu, Yunan harflerinden ile simgelendiği için Fi fonksiyonu olarak da anılabilir.

Örneğin, ; zira 10 ile dört sayma sayısı, hem 10'dan küçüktür, hem de 10 ile arasında asaldır: 1, 3, 7 ve 9.
Euler fonksiyonu, de kullanılır. Şöyle ki:
, a ile n aralarında asal ise. Dolayısıyla, , n'in bir tam katıdır.
Örneğin, , için sırasıyla , 10'un bir tam katıdır.
Totient fonksiyonu ayrıca RSA kriptografi sisteminde de kilit rol oynamaktadır.
Totient fonksiyonunun hesaplanması
Fonksiyonun yukarıda verilen tanımına göre 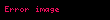
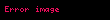



için
Yukarıdaki formül bir Euler Çarpımı'dır ve genellikle

şeklinde yazılır.
Hesaplama Örneği
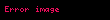
Yani yazıyla ifade edersek, 36'nın asal çarpanları 2 ve 3'tür. 36'nın yarısı olan 18 tane sayı 2 ile bölünür, dolayısıyla 36 ile aralarında asal değildir. Kalan 18 sayının da 3'te biri 3 ile bölünür. Bu durumda 36 sayı içerisinde 36 ile aralarında asal olan sadece 12 sayı kalır.
Fonksiyonun Bazı Değerleri
İlk birkaç değer aşağıdaki tabloda ve grafikte gösterilmiştir:

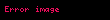 | +0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0+ | 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | |
| 10+ | 4 | 10 | 4 | 12 | 6 | 8 | 8 | 16 | 6 | 18 |
| 20+ | 8 | 12 | 10 | 22 | 8 | 20 | 12 | 18 | 12 | 28 |
| 30+ | 8 | 30 | 16 | 20 | 16 | 24 | 12 | 36 | 18 | 24 |
| 40+ | 16 | 40 | 12 | 42 | 20 | 24 | 22 | 46 | 16 | 42 |
| 50+ | 20 | 32 | 24 | 52 | 18 | 40 | 24 | 36 | 28 | 58 |
| 60+ | 16 | 60 | 30 | 36 | 32 | 48 | 20 | 66 | 32 | 44 |
| 70+ | 24 | 70 | 24 | 72 | 36 | 40 | 36 | 60 | 24 | 78 |
| 80+ | 32 | 54 | 40 | 82 | 24 | 64 | 42 | 56 | 40 | 88 |
| 90+ | 24 | 72 | 44 | 60 | 46 | 72 | 32 | 96 | 42 | 60 |
Fonksiyonun Özellikleri
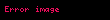
Buradaki toplam nnin tüm d pozitif bölenlerine kadar genişler.
Şimdi Möbius formülünü, bu toplamı değiştirmek ve 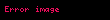
Burada, μ pozitif tam sayılarda tanımlanan Möbius fonksiyonudur.
Euler'in teoremine göre, eğer a ile n aralarında asallarsa, yani ebob(a, n) = 1,
Bu durum Lagrange'ın teoremini ve anın 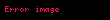
Formül Geliştirilmesi
Burada gösterilen iki fonksiyon da
nın sonucudur.

öyle ki ζ(s) Rienmann Zeta Fonksiyonudur. Bunun ispatı aşağıda gösterildiği gibidir:
Lambert serisi fonksiyonu,
öyle ki |q|<1 için ıraksar.
Bu durumun nedeni
yani
Fonksiyonun Büyümesi
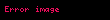
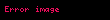
(herhangi bir ε > 0 ve n > N(ε) için)
Aslında
ele alınırsa,
yazılabilir. p|ni sağlayan p asal sayıları için)
Asal sayı teoremi'nden εnin yerine aşağıdakinin yazılabileceği gösterilebilir:

Yani


ile gösterilir; çünkü 
Euler Totient Fonksiyonu'nu İçeren Diğer Formüller
Burada m > 1 bir pozitif tam sayıdır ve ω(m) min asal sayı çarpanlarını ifade eder. (Bu formül nden küçük ve m ile aralarında asal olan doğal sayıların sayısını gösterir.)
Eşitsizlikler

n > 2 için, &gamma Euler sabiti iken,
n için > 0,
ve
n asal sayısı için, açıkça 
n birleşik sayısı için
.
Rastgele büyüklükteki n için, bu sınırlar halen geliştirilememeiştir ya da daha kesin olmak gerekirse:


Ford'un Teoremi
Ford, her k ≥ 2 tam sayısı için φ(x) = m eşitliğinin tam olarak k sağlayanı bulunması durumunu sağlayan bir m sayısının bulunduğunu ispatladı. Ne yazık ki, k = 1 için herhangi bir m bulunamamıştır, Carmichal'ın Totient Fonksiyonu Konjektürü'ne göre, bu durumda böyle bir min varolmadığına inanılır.
Kaynakça
- ; (1964), Handbook of Mathematical Functions, New York: Dover Publications, ISBN . See paragraph 24.3.2.
- ; (1996), Algorithmic Number Theory, 1, Cambridge, MA: MIT Press, ISBN . See page 234 in section 8.8.
- Ford, K. (1999), "The number of solutions of φ(x) = m", , 150 (1), ss. 283-311, doi:10.2307/121103, 1715326.
- Schramm, Wolfgang (2008), "The Fourier transform of functions of the greatest common divisor", Electronic Journal of Combinatorial Number Theory, A50 (8(1)), 1 Mayıs 2009 tarihinde kaynağından , erişim tarihi: 29 Nisan 2009.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Totient kisaca f n sayilar teorisinde bir tam sayinin o sayidan daha kucuk ve o sayi ile aralarinda asal olan sayma sayi sayisini belirten fonksiyondur Genellikle Euler Totient ya da Euler in Totienti olarak adlandirilan Totient Isvicreli matematikci Leonhard Euler tarafindan yaratilmistir Totient fonksiyonu Yunan harflerinden f displaystyle varphi ile simgelendigi icin Fi fonksiyonu olarak da anilabilir f n fonksiyonun ilk 1000 degeri Ornegin f 10 4 displaystyle varphi 10 4 zira 10 ile dort sayma sayisi hem 10 dan kucuktur hem de 10 ile arasinda asaldir 1 3 7 ve 9 Euler fonksiyonu de kullanilir Soyle ki af n 1 modn displaystyle a varphi n equiv 1 pmod n a ile n aralarinda asal ise Dolayisiyla af n 1 displaystyle a varphi n 1 n in bir tam katidir Ornegin a4 1 displaystyle a 4 1 a 1 3 7 9 displaystyle a 1 3 7 9 icin sirasiyla 0 80 2400 6560 displaystyle 0 80 2400 6560 10 un bir tam katidir Totient fonksiyonu ayrica RSA kriptografi sisteminde de kilit rol oynamaktadir Totient fonksiyonunun hesaplanmasiFonksiyonun yukarida verilen tanimina gore f 1 1 displaystyle varphi 1 1 ve eger p bir asal sayiysa f pk p 1 pk 1 displaystyle varphi p k p 1 p k 1 Bunun yaninda totient fonksiyonunun carpim ozelligi de vardir m ve n aralarinda asallarsa f mn f m f n displaystyle varphi mn varphi m varphi n Bu yarginin ispatinin anahatti A B ve C kumeleri sirasiyla m n ve mn ile aralarinda asal ve modlarinin kalan kumesi olsun Bu durumda yararlanilirsa gourulur ki AxB ve C arasinda esleme olur Yani f displaystyle varphi fonksiyonunun degeri aritmetigin temel teoremi kullanilarak hesaplanabilir Oyleyse n p1k1 prkr displaystyle n p 1 k 1 cdots p r k r icin f n p1 1 p1k1 1 pr 1 prkr 1 displaystyle varphi n p 1 1 p 1 k 1 1 cdots p r 1 p r k r 1 Yukaridaki formul bir Euler Carpimi dir ve genellikle f n n p n 1 1p displaystyle varphi n n cdot prod p n left 1 frac 1 p right seklinde yazilir Hesaplama Ornegi f 36 f 3222 36 1 13 1 12 36 23 12 12 displaystyle varphi 36 varphi left 3 2 2 2 right 36 left 1 frac 1 3 right left 1 frac 1 2 right 36 cdot frac 2 3 cdot frac 1 2 12 Yani yaziyla ifade edersek 36 nin asal carpanlari 2 ve 3 tur 36 nin yarisi olan 18 tane sayi 2 ile bolunur dolayisiyla 36 ile aralarinda asal degildir Kalan 18 sayinin da 3 te biri 3 ile bolunur Bu durumda 36 sayi icerisinde 36 ile aralarinda asal olan sadece 12 sayi kalir Fonksiyonun Bazi DegerleriIlk birkac deger asagidaki tabloda ve grafikte gosterilmistir Ilk 100 degerin grafige dokumuf n displaystyle varphi n 0 1 2 3 4 5 6 7 8 90 1 1 2 2 4 2 6 4 610 4 10 4 12 6 8 8 16 6 1820 8 12 10 22 8 20 12 18 12 2830 8 30 16 20 16 24 12 36 18 2440 16 40 12 42 20 24 22 46 16 4250 20 32 24 52 18 40 24 36 28 5860 16 60 30 36 32 48 20 66 32 4470 24 70 24 72 36 40 36 60 24 7880 32 54 40 82 24 64 42 56 40 8890 24 72 44 60 46 72 32 96 42 60Fonksiyonun Ozelliklerif n displaystyle varphi n sayisi ayni zamanda dairesel grup olan Cnnin olasi generatorlerine esittir Bu nedenleCnin her elemani bir dairesel altgrup olusturur Cnnin algruplari Cd formundadir eger d boler n d n seklinde yazilir Boylece d nf d n displaystyle sum d mid n varphi d n Buradaki toplam nnin tum d pozitif bolenlerine kadar genisler Simdi Mobius formulunu bu toplami degistirmek ve f n displaystyle varphi n icin bir formul daha elde etmek icin kullanabiliriz f n d nd m nd displaystyle varphi n sum d mid n d cdot mu left frac n d right Burada m pozitif tam sayilarda tanimlanan Mobius fonksiyonudur Euler in teoremine gore eger a ile n aralarinda asallarsa yani ebob a n 1 af n 1modn displaystyle a varphi n equiv 1 mod n Bu durum Lagrange in teoremini ve anin Z nZ displaystyle mathbb Z n mathbb Z nin mod n e gore tam sayi grubuna ait olmasini takip eder Ancak ve ancak a ile n aralarinda asallarsa Formul GelistirilmesiBurada gosterilen iki fonksiyon da d nf d n displaystyle sum d n varphi d n nin sonucudur f displaystyle varphi n yi iceren bir Dirichlet Serisi n 1 f n ns z s 1 z s displaystyle sum n 1 infty frac varphi n n s frac zeta s 1 zeta s oyle ki z s Rienmann Zeta Fonksiyonudur Bunun ispati asagida gosterildigi gibidir z s f 1 f f fs g 1 1gs f 1 f f fs displaystyle zeta s sum f 1 infty frac varphi f f s left sum g 1 infty frac 1 g s right left sum f 1 infty frac varphi f f s right g 1 1gs f 1 f f fs h 1 fg h1 f g 1hs displaystyle left sum g 1 infty frac 1 g s right left sum f 1 infty frac varphi f f s right sum h 1 infty left sum fg h 1 cdot varphi g right frac 1 h s h 1 fg hf g 1hs h 1 d hf d 1hs displaystyle sum h 1 infty left sum fg h varphi g right frac 1 h s sum h 1 infty left sum d h varphi d right frac 1 h s h 1 d hf d 1hs displaystyle sum h 1 infty left sum d h varphi d right frac 1 h s h 1 hhs displaystyle sum h 1 infty frac h h s h 1 hhs z s 1 displaystyle sum h 1 infty frac h h s zeta s 1 Lambert serisi fonksiyonu n 1 f n qn1 qn q 1 q 2 displaystyle sum n 1 infty frac varphi n q n 1 q n frac q 1 q 2 oyle ki q lt 1 icin iraksar Bu durumun nedeni n 1 f n qn1 qn n 1 f n r 1qrn displaystyle sum n 1 infty frac varphi n q n 1 q n sum n 1 infty varphi n sum r geq 1 q rn yani k 1qk n kf n k 1kqk q 1 q 2 displaystyle sum k geq 1 q k sum n k varphi n sum k geq 1 kq k frac q 1 q 2 Fonksiyonun Buyumesif n displaystyle varphi n nin fonksiyon olarak buyumesi ilginc bir sorudur cunku kucuknler icin f n displaystyle varphi n in nden kucuk olacagi dusuncesi tam olarak dogru degildir Asimptotik olarak n1 e lt f n lt n displaystyle n 1 varepsilon lt varphi n lt n herhangi bir e gt 0 ve n gt N e icin Aslinda f n n displaystyle varphi n n ele alinirsa 1 p 1 displaystyle 1 p 1 yazilabilir p ni saglayan p asal sayilari icin Asal sayi teoremi nden enin yerine asagidakinin yazilabilecegi gosterilebilir Clog log n log n displaystyle C log log n log n f displaystyle varphi de ortalama olarak ne yakindir 1n2 k 1nf k 3p2 O log nn displaystyle frac 1 n 2 sum k 1 n varphi k frac 3 pi 2 mathcal O left frac log n n right Yani 1 2 n displaystyle 1 2 ldots n ndan rastgele secilen iki pozitif sayinin aralarinda asal olma olasiligi n sonsuza yaklasirken 6p2 displaystyle frac 6 pi 2 a yaklasir Bununla ilgili bir sonuc da 1n k 1nf k k 6p2 O log nn displaystyle frac 1 n sum k 1 n frac varphi k k frac 6 pi 2 mathcal O left frac log n n right ile gosterilir cunku 6p2 1z 2 displaystyle frac 6 pi 2 frac 1 zeta 2 formul bu sekilde de ifade edilebilir 1n k 1nf k k 1z 2 O log nn displaystyle frac 1 n sum k 1 n frac varphi k k frac 1 zeta 2 mathcal O left frac log n n right Euler Totient Fonksiyonu nu Iceren Diger Formullerf nm nm 1f n for m 1 displaystyle varphi left n m right n m 1 varphi n text for m geq 1 herhangi a n gt 1 oyle vardir kil n oyledir ki l f an 1 displaystyle text herhangi a n gt 1 text oyle vardir ki l geq n text oyledir ki l varphi a n 1 Herhangi a gt 1 ve n gt 6 oyle vardir ki 4 n oyledir ki l 2n oyledir ki l f an 1 displaystyle text Herhangi a gt 1 text ve n gt 6 text oyle vardir ki 4 not n text oyledir ki l geq 2n text oyledir ki l varphi a n 1 d nm2 d f d nf n displaystyle sum d mid n frac mu 2 d varphi d frac n varphi n 1 k n k n 1k 12nf n for n gt 1 displaystyle sum 1 leq k leq n atop k n 1 k frac 1 2 n varphi n text for n gt 1 k 1nf k 12 1 k 1nm k nk 2 displaystyle sum k 1 n varphi k frac 1 2 left 1 sum k 1 n mu k left lfloor frac n k right rfloor 2 right k 1nf k k k 1nm k k nk displaystyle sum k 1 n frac varphi k k sum k 1 n frac mu k k left lfloor frac n k right rfloor k 1nkf k O n displaystyle sum k 1 n frac k varphi k mathcal O n k 1n1f k O log n displaystyle sum k 1 n frac 1 varphi k mathcal O log n 1 k n k m 11 nf m m O 2w m displaystyle sum 1 leq k leq n atop k m 1 1 n frac varphi m m mathcal O left 2 omega m right Burada m gt 1 bir pozitif tam sayidir ve w m min asal sayi carpanlarini ifade eder Bu formul nden kucuk ve m ile aralarinda asal olan dogal sayilarin sayisini gosterir Esitsizliklerf displaystyle varphi fonksiyonunu iceren bazi esitsizlikler f n gt neglog log n 3log log n displaystyle varphi n gt frac n e gamma log log n frac 3 log log n n gt 2 icin amp gamma Euler sabiti iken f n n2 displaystyle varphi n geq sqrt frac n 2 n icin gt 0 ve f n n for n gt 6 displaystyle varphi n geq sqrt n text for n gt 6 n asal sayisi icin acikca f n n 1 displaystyle varphi n n 1 n birlesik sayisi icin f n n n displaystyle varphi n leq n sqrt n Rastgele buyuklukteki n icin bu sinirlar halen gelistirilememeistir ya da daha kesin olmak gerekirse lim inff n n 0 ve lim supf n n 1 displaystyle liminf frac varphi n n 0 mbox ve limsup frac varphi n n 1 f displaystyle varphi fonksiyonu ile s displaystyle sigma fonksiyonunu birlestiren birkac esitsizlik 6n2p2 lt f n s n lt n2 icin n gt 1 displaystyle frac 6n 2 pi 2 lt varphi n sigma n lt n 2 mbox icin n gt 1 Ford un TeoremiFord her k 2 tam sayisi icin f x m esitliginin tam olarak k saglayani bulunmasi durumunu saglayan bir m sayisinin bulundugunu ispatladi Ne yazik ki k 1 icin herhangi bir m bulunamamistir Carmichal in Totient Fonksiyonu Konjekturu ne gore bu durumda boyle bir min varolmadigina inanilir Kaynakca 1964 Handbook of Mathematical Functions New York Dover Publications ISBN 0 486 61272 4 See paragraph 24 3 2 1996 Algorithmic Number Theory 1 Cambridge MA MIT Press ISBN 0 262 02405 5 See page 234 in section 8 8 Ford K 1999 The number of solutions of f x m 150 1 ss 283 311 doi 10 2307 121103 1715326 Schramm Wolfgang 2008 The Fourier transform of functions of the greatest common divisor Electronic Journal of Combinatorial Number Theory A50 8 1 1 Mayis 2009 tarihinde kaynagindan erisim tarihi 29 Nisan 2009
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans