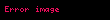Matematiğin bir alt dalı olan olasılık teorisinde ve , filtre ya da süzgeç azalmayan bir ailesidir. Amerikalı matematikçi tarafından 1953'te literatüre sokulmuştur.
Tanım






Bir rassal sürecin doğal süzgeci
Bir olasılık uzayı üzerinde tanımlanan 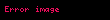
.
O zaman, 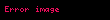
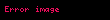
Süzgeçle ilgili diğer tanımlar
Süreklilik
Bir olasılık uzayının süzgecinin soldan ve sürekli olması kavramı bazen değişik sonuçlarda teknik gereklilik olarak yazılır.



- Her
için,
- Her
için,
tanımlayalım. O halde, her 
ise
süzgeci sağdan sürekli
ise
süzgeci soldan sürekli
denir. Bir süzgeç hem sağdan hem de soldan sürekliyse, o zaman bu süzgeçe sürekli süzgeç denir.
Tam süzgeçler


tanımlayalım. Yani, 





Artırılmış süzgeçler
Sağdan sürekli ve tam olan süzgeçlere artırılmış süzgeçler denir. Eğer bir süzgeç artılmış süzgeçse, süzgeç olağan koşulları sağlar kullanımı da vardır.
Ayrıca bakınız
Notlar
- ^ Doob 1953, s. 294'te (Chapter VII Martingales kısmında) açıkça görülmektedir.
- ^ Snell 1991
- ^ Coculescu & Nikeghbali 2010
- ^ Karatzas & Shreve 1991, s. 4
Kaynakça
- Coculescu, Dalia; Nikeghbali, Ashkan (2010), "Filtrations", Encyclopedia of Quantitative Finance, cilt 2, ss. 683-686, erişim tarihi: 6 Eylül 2024
- (1953), Stochastic processes, New York: , MR 0058896
- Karatzas, Ioannis; (1991), Brownian Motion and Stochastic Calculus, 2nd, Springer-Verlag, ISBN
- Snell, J. L. (1997), "A conversation with Joe Doob", Statist. Sci., 12 (4), ss. 301-311, erişim tarihi: 4 Eylül 2024
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan olasilik teorisinde ve filtre ya da suzgec azalmayan bir ailesidir Amerikali matematikci tarafindan 1953 te literature sokulmustur Tanim W F P displaystyle Omega mathcal F mathbb P bir olasilik uzayi ve T R displaystyle T subset mathbb R olsun Eger bir s cebiri ailesi Ft t T displaystyle mathcal F t t in T icin Fs Ft F s t s t T displaystyle mathcal F s subset mathcal F t subset mathcal F forall s leq t s t in T saglaniyorsa Ft t T displaystyle mathcal F t t in T ye W F P displaystyle Omega mathcal F mathbb P olasilik uzayinin bir filtresi ya da suzgeci denir Bir rassal surecin dogal suzgeciBir olasilik uzayi uzerinde tanimlanan Xt t T displaystyle X t t in T rassal sureci icin asagidaki gibi bir ailesi tanimlansin FtX s Xs s t s T t T displaystyle mathcal F t X sigma X s mid s leq t s in T quad t in T O zaman FtX t T displaystyle left mathcal F t X right t in T bir suzgec olur ve buna Xt t T displaystyle X t t in T rassal surecinin dogal suzgeci denir Suzgecle ilgili diger tanimlarSureklilikBir olasilik uzayinin suzgecinin soldan ve surekli olmasi kavrami bazen degisik sonuclarda teknik gereklilik olarak yazilir W F P displaystyle Omega mathcal F mathbb P bir olasilik uzayi T 0 displaystyle T 0 infty ve Ft t 0 displaystyle mathcal F t t geq 0 de bu olasilik uzayinin suzgeci olsun Her t gt 0 displaystyle t gt 0 icin Ft s s lt tFs displaystyle mathcal F t sigma left bigcup s lt t mathcal F s right F0 F0 displaystyle mathcal F 0 mathcal F 0 Her t 0 displaystyle t geq 0 icin Ft s e gt 0Fs e displaystyle mathcal F t sigma left bigcap varepsilon gt 0 mathcal F s varepsilon right tanimlayalim O halde her t 0 displaystyle t geq 0 icin Ft t Ft t displaystyle mathcal F t t mathcal F t t ise Ft t 0 displaystyle mathcal F t t geq 0 suzgeci sagdan surekli Ft t Ft t displaystyle mathcal F t t mathcal F t t ise Ft t 0 displaystyle mathcal F t t geq 0 suzgeci soldan surekli denir Bir suzgec hem sagdan hem de soldan surekliyse o zaman bu suzgece surekli suzgec denir Tam suzgecler W F P displaystyle Omega mathcal F mathbb P bir olasilik uzayi ve Ft t I displaystyle mathbb mathcal F t t in I bu uzayin bir suzgeci olsun N N W A F N A P A 0 displaystyle mathcal N N subset Omega mid exists A in mathcal F N subset A wedge P A 0 tanimlayalim Yani N displaystyle mathcal N P displaystyle P altkumesi olan kumelerin kumsesidir Her t T displaystyle t in T icin N Ft displaystyle mathcal N in mathcal F t saglanirsa W Ft P displaystyle Omega mathcal F t P uzayi tam bir olcu uzayi olur ve Ft t I displaystyle mathbb mathcal F t t in I tam suzgec denir Artirilmis suzgeclerSagdan surekli ve tam olan suzgeclere artirilmis suzgecler denir Eger bir suzgec artilmis suzgecse suzgec olagan kosullari saglar kullanimi da vardir Ayrica bakinizMartingalNotlar Doob 1953 s 294 te Chapter VII Martingales kisminda acikca gorulmektedir Snell 1991 Coculescu amp Nikeghbali 2010 Karatzas amp Shreve 1991 s 4KaynakcaCoculescu Dalia Nikeghbali Ashkan 2010 Filtrations Encyclopedia of Quantitative Finance cilt 2 ss 683 686 erisim tarihi 6 Eylul 2024 1953 Stochastic processes New York John Wiley amp Sons Inc MR 0058896 Karatzas Ioannis 1991 Brownian Motion and Stochastic Calculus 2nd Springer Verlag ISBN 978 0 387 97655 6 Snell J L 1997 A conversation with Joe Doob Statist Sci 12 4 ss 301 311 erisim tarihi 4 Eylul 2024
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans