Fleiss'in kappa katsayısı ikiden fazla sabit sayıda değerleyici arasındaki karşılaştırmalı uyuşmanın güvenirliğini ölçen bir istatistik yöntemidir. Fleiss'in kappa ölçüsü sabit sayıda (n tane) değerleyicinin her birinin, (N tane) maddeyi veya kişiyi (C tane) birbirinden karşılıklı hariç olan kategoriye göre ayırmaları süreci sonunda ortaya çıkan değerleyiciler arasındaki uyuşmayı ölçer. Fleiss'in kappa ölçüsü bu uyuşmanın bir şans eseri olabileceğini de ele aldığı için basit yüzde orantı olarak bulunan uyuşmadan daha güçlü bir sonuç verdiği kabul edilir. Ortaya çıkan kategorik değişken olduğu için Fleiss'in kappa katsayısı bir parametrik olmayan istatistik türüdür.
Fleiss'in kappa katsayısı iki değerleyicinin uyuşmaları sorunu inceleyen nın bir genelleştirilmesidir. Benzer şekilde Cohen'in kappa katsayısına da ilişkilidir. Ancak ve Cohen'in kappa katsayısı iki değerleyici olması gerektirirken, Fleiss'in kappa katsayısı ikiden daha çok herhangi bir sayıda değerleyici için uygulanabilir. Aynı onlar gibi, yine sabit sayıda değerleyicinin aralarındaki uyuşmanın ne kadar rastgelelik eseri olmadığı ve bu nedenle ne kadar güvenilir olduğunun sayısal olarak 0 ve 1 değerleri arasında ifade edilmektedir.
Açıklamalar
Bu konu şöyle daha genişletilebilir: Sabit n sayıda değerleyici vardır; bunların inceledikleri değerlendikleri haller N sayıdadır; her bir değerleyici her bir hal için k sayıda kategori sayısı verecektir. Eğer bir hal için iki değişik değerleyici aynı kategori sayısı vermişlerse, bu iki değerleyicinin uyuştuğunu gösterir; eğer kategori sayısı değişikse verilen kategori sayıları arasındaki farka dayanarak değişik derecede uyuşmazlık bulunur. Bu uyuşma ya rastgelelik sonucunda doğmuştur yahut da değerleyicilerin inanç ve davranışları birbirine benzemektedir. Fleiss'in kappa katsayısı tek bir hal için iki tane değerleyiciyi değil; n tane değerleyici tarafından N tane hal için yapılan değerlendirmelerle ilgilidir ve bu değerlendirmeler arasındaki uyuşmanın ne derecede rastgelelikten ayrıldığının sayısal ifadesidir.
Fleiss'in kappa katsayısı şöyle tanımlanmıştır:
Burada 

Aşağıda Fleiss'in kappa katsayısını bulmak için hesaplar için örneğinde şu araştırma sorunu ele alınmaktadır:
- Büyük bir psikiyatri kliniği olan bir hastanede 10 hasta için 14 tane doktor ve psikiyatrist tedavi için hastaları 5 kategoride değerlendirmektedirler. Her hasta için her doktor/psikiyatrist beş kategoriden birini seçmektedir. Bu değerlendirmeler bir tabloda aşağıda verilmiştir. Fleiss'in kappa katsayısı bulunup doktor/psikiyatristlerin değerlendirmelerinde kendi aralarında, şans eseri olmayan bir şekilde, ne ölçüde uyuştukları incelenecektir.
Formüller
N değerlendirilecek hallerin sayısı; n toplam değerleyici sayısı ve k ise degerlemede kullanılacak kategori sayısı olsun. Haller i indeks sayısı ile belirlensin i=1,...,N; değer kategorileri j ile indekslensin j=1,...,k. niji-inci hali j-inci kategoriye koyan değerleyici sayısını temsil etmektedir.
- Önce j-inci kategoriye koyulmuş değerlendirme oranı,
olarak, hesaplanır:
(1)
- Sonra i-inci hal için değerleyicilerin ne derece uyuştuklarını gösteren
, hesaplanır:
(2)
- Simdi
lerin ortalaması olan
hesaplanır:
(3)
- En son toplam ortalama
olan
hesaplanır:
(4)
- Sonuç olarak bunlar yukarıda verilen formüle konulup Fleiss'in kappa katsayısı bulunur:
(5)
Fleiss'in kappa katsayisi için şu değerler hemen yorumlanır:
- κ=1 : Tum değerleyiciler hep birlikte birbirine uyuşmaktadırlar.
- κ=0 : Değerleyiciler aralarında uyuşmalar sadece şans ile belirlenmiştir ve diğer hallerde hiçbir uyuşma yoktur.
Örneğin
Veri serisi
Yukarıdaki örnekte 14 tane değerleyici (yani n=14), 10 sayıda bir örneklem hallerini (yani N=10) değerlendirip 5 kategoriye (yani k=5) ayırmaktadırlar. Aşağıda örneklem halleri satırlarda ve kategorilerde sütunlarda gösterilmiştir. Burada kullanılan kutuçizim girdileri ve hesap sonuçları verilecektir:
| 1 | 2 | 3 | 4 | 5 |  | |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 14 | 1.000 |
| 2 | 0 | 2 | 6 | 4 | 2 | 0.253 |
| 3 | 0 | 0 | 3 | 5 | 6 | 0.308 |
| 4 | 0 | 3 | 9 | 2 | 0 | 0.440 |
| 5 | 2 | 2 | 8 | 1 | 1 | 0.330 |
| 6 | 7 | 7 | 0 | 0 | 0 | 0.462 |
| 7 | 3 | 2 | 6 | 3 | 0 | 0.242 |
| 8 | 2 | 5 | 3 | 2 | 2 | 0.176 |
| 9 | 6 | 5 | 2 | 1 | 0 | 0.286 |
| 10 | 0 | 2 | 2 | 3 | 7 | 0.286 |
| Total | 20 | 28 | 39 | 21 | 32 | |
 | 0.143 | 0.200 | 0.279 | 0.150 | 0.229 |
Veri özetleri şunlardır: 


Tüm gözlemler için toplam = 140
Formül ve hesaplar
Birinci kategori sütunu toplamı için toplam orantı şöyle bulunur:
İkinci satır hali için toplam orantı şöyle bulunur:


Tüm veri serisi ve hesaplama sayfası için
Sonuç olarak Kappa formülü kullanılır:
Sonuç yorumlaması
Landis ve Koch (1977) elde edilen 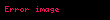
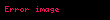 | Yorum |
|---|---|
| < 0 | Hiç uyuşma olmaması |
| 0.0 — 0.20 | Önemsiz uyuşma olması |
| 0.21 — 0.40 | Orta derecede uyuşma olması |
| 0.41 — 0.60 | Ekseriyetle uyuşma olması |
| 0.61 — 0.80 | Önemli derecede uyuşma olması |
| 0.81 — 1.00 | Neredeyse mükemmel uyuşma olması |
Verilen örneğinde
bulunduğu için ancak orta dereceli bir uyuşma olduğu sonucu çıkarılabilir.
Ancak bu tabloda verilen yorumlar ve hatta verilen aralıklar hakkında istatistikçiler arasında anlaşmazlık vardır. Landis ve Koch yazılarında verdikleri aralıklar ve yorumlar için teorik delil vermemişlerdir ve bu ifadeler ancak birer şahsi inanç olarak kabul edilebilirler. Bazı istatistikçilere göre bu aralıklar ve yorumlar araştırmacılara zararlı olabilirler. . Bu aralıklar ve yorumlar araştırıcılara Kappa değerinin değişken kategori sayısından da (yani Cden) etkilendiği gerçeğini unutturabilir. Bilinmektedir ki kategori sayısı ne kadar küçük olursa kappa değeri de büyük olmaktadır.
İçsel kaynaklar

- Cohen'in kappa katsayısı
- (Pearson'un çarpım-moment korelasyon katsayısı)
Kaynakça
- ^ Fleiss,J.L.(1971) "Measuring nominal scale agreement among many raters." Psychological Bulletin, Cilt 76, Sayi 5 say. 378-382
- ^ * Scott, W. (1955). "Reliability of content analysis: The case of nominal scale coding." Public Opinion Quarterly, Cilt 19, Sayi 3, say.321-325
- ^ Cohen, J. (1960), A coefficient of agreement for nominal scales, Educational and Psychological Measurement Cilt 20, Sayi 1, say.37-46
- ^ Landis, J. R. ve Koch, G. G. (1977) "The measurement of observer agreement for categorical data", Biometrics. Cilt. 33, say. 159-174
- ^ Gwet, K. (2001) Statistical Tables for Inter-Rater Agreement. (Gaithersburg : StatAxis Publishing)
- ^ Sim, J. and Wright, C. C. (2005) "The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requirements" in Physical Therapy. Cilt. 85, say. 257--268
Dış bağlantılar
- Katsayı hakkında kapsamlı bir makaleler bibliyografyası vermektedir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fleiss in kappa katsayisi ikiden fazla sabit sayida degerleyici arasindaki karsilastirmali uyusmanin guvenirligini olcen bir istatistik yontemidir Fleiss in kappa olcusu sabit sayida n tane degerleyicinin her birinin N tane maddeyi veya kisiyi C tane birbirinden karsilikli haric olan kategoriye gore ayirmalari sureci sonunda ortaya cikan degerleyiciler arasindaki uyusmayi olcer Fleiss in kappa olcusu bu uyusmanin bir sans eseri olabilecegini de ele aldigi icin basit yuzde oranti olarak bulunan uyusmadan daha guclu bir sonuc verdigi kabul edilir Ortaya cikan kategorik degisken oldugu icin Fleiss in kappa katsayisi bir parametrik olmayan istatistik turudur Fleiss in kappa katsayisi iki degerleyicinin uyusmalari sorunu inceleyen nin bir genellestirilmesidir Benzer sekilde Cohen in kappa katsayisina da iliskilidir Ancak ve Cohen in kappa katsayisi iki degerleyici olmasi gerektirirken Fleiss in kappa katsayisi ikiden daha cok herhangi bir sayida degerleyici icin uygulanabilir Ayni onlar gibi yine sabit sayida degerleyicinin aralarindaki uyusmanin ne kadar rastgelelik eseri olmadigi ve bu nedenle ne kadar guvenilir oldugunun sayisal olarak 0 ve 1 degerleri arasinda ifade edilmektedir AciklamalarBu konu soyle daha genisletilebilir Sabit n sayida degerleyici vardir bunlarin inceledikleri degerlendikleri haller N sayidadir her bir degerleyici her bir hal icin k sayida kategori sayisi verecektir Eger bir hal icin iki degisik degerleyici ayni kategori sayisi vermislerse bu iki degerleyicinin uyustugunu gosterir eger kategori sayisi degisikse verilen kategori sayilari arasindaki farka dayanarak degisik derecede uyusmazlik bulunur Bu uyusma ya rastgelelik sonucunda dogmustur yahut da degerleyicilerin inanc ve davranislari birbirine benzemektedir Fleiss in kappa katsayisi tek bir hal icin iki tane degerleyiciyi degil n tane degerleyici tarafindan N tane hal icin yapilan degerlendirmelerle ilgilidir ve bu degerlendirmeler arasindaki uyusmanin ne derecede rastgelelikten ayrildiginin sayisal ifadesidir Fleiss in kappa katsayisi soyle tanimlanmistir k P Pe 1 Pe displaystyle kappa frac bar P bar P e 1 bar P e Burada 1 Pe displaystyle 1 bar P e faktoru rastgelelik otesinde ne derece uyusma olabilmesinin mumkun oldugunu gosterir P Pe displaystyle bar P bar P e gozlemlenen gercekte ne derecede rastgelelik otesinde uyusma derecesinin ortaya ciktigini aciklar Asagida Fleiss in kappa katsayisini bulmak icin hesaplar icin orneginde su arastirma sorunu ele alinmaktadir Buyuk bir psikiyatri klinigi olan bir hastanede 10 hasta icin 14 tane doktor ve psikiyatrist tedavi icin hastalari 5 kategoride degerlendirmektedirler Her hasta icin her doktor psikiyatrist bes kategoriden birini secmektedir Bu degerlendirmeler bir tabloda asagida verilmistir Fleiss in kappa katsayisi bulunup doktor psikiyatristlerin degerlendirmelerinde kendi aralarinda sans eseri olmayan bir sekilde ne olcude uyustuklari incelenecektir FormullerN degerlendirilecek hallerin sayisi n toplam degerleyici sayisi ve k ise degerlemede kullanilacak kategori sayisi olsun Haller i indeks sayisi ile belirlensin i 1 N deger kategorileri j ile indekslensin j 1 k niji inci hali j inci kategoriye koyan degerleyici sayisini temsil etmektedir Once j inci kategoriye koyulmus degerlendirme orani pj displaystyle p j olarak hesaplanir 1 pj 1Nn i 1Nnij 1 1n j 1knij displaystyle p j frac 1 Nn sum i 1 N n ij quad quad 1 frac 1 n sum j 1 k n ij Sonra i inci hal icin degerleyicilerin ne derece uyustuklarini gosteren Pi displaystyle P i hesaplanir 2 Pi 1n n 1 j 1knij nij 1 displaystyle P i frac 1 n n 1 sum j 1 k n ij n ij 1 1n n 1 j 1k nij2 nij displaystyle frac 1 n n 1 left sum j 1 k n ij 2 n ij right dd 1n n 1 j 1knij2 n displaystyle frac 1 n n 1 left sum j 1 k n ij 2 n right dd Simdi Pi displaystyle P i lerin ortalamasi olan P displaystyle bar P hesaplanir 3 P 1N i 1NPi displaystyle bar P frac 1 N sum i 1 N P i 1Nn n 1 i 1N j 1knij2 Nn displaystyle frac 1 Nn n 1 left sum i 1 N sum j 1 k n ij 2 Nn right dd En son toplam ortalama j 1kpj2 displaystyle sum j 1 k p j 2 olan Pe displaystyle bar P e hesaplanir 4 Pe j 1kpj2 displaystyle bar P e sum j 1 k p j 2 Sonuc olarak bunlar yukarida verilen formule konulup Fleiss in kappa katsayisi bulunur 5 k P Pe 1 Pe displaystyle kappa frac bar P bar P e 1 bar P e Fleiss in kappa katsayisi icin su degerler hemen yorumlanir k 1 Tum degerleyiciler hep birlikte birbirine uyusmaktadirlar k 0 Degerleyiciler aralarinda uyusmalar sadece sans ile belirlenmistir ve diger hallerde hicbir uyusma yoktur OrneginVeri serisi Yukaridaki ornekte 14 tane degerleyici yani n 14 10 sayida bir orneklem hallerini yani N 10 degerlendirip 5 kategoriye yani k 5 ayirmaktadirlar Asagida orneklem halleri satirlarda ve kategorilerde sutunlarda gosterilmistir Burada kullanilan kutucizim girdileri ve hesap sonuclari verilecektir 1 2 3 4 5 Pi displaystyle P i 1 0 0 0 0 14 1 0002 0 2 6 4 2 0 2533 0 0 3 5 6 0 3084 0 3 9 2 0 0 4405 2 2 8 1 1 0 3306 7 7 0 0 0 0 4627 3 2 6 3 0 0 2428 2 5 3 2 2 0 1769 6 5 2 1 0 0 28610 0 2 2 3 7 0 286Total 20 28 39 21 32pj displaystyle p j 0 143 0 200 0 279 0 150 0 229Ornegin icin hesaplamalar icin veriler tablosu Veri ozetleri sunlardir N displaystyle N 10 n displaystyle n 14 k displaystyle k 5 Tum gozlemler icin toplam 140 Pi displaystyle P i icin toplam 3 780 Formul ve hesaplar Birinci kategori sutunu toplami icin toplam oranti soyle bulunur p1 0 0 0 0 2 7 3 2 6 0 140 0 143 displaystyle p 1 frac 0 0 0 0 2 7 3 2 6 0 140 0 143 Ikinci satir hali icin toplam oranti soyle bulunur P2 114 14 1 02 22 62 42 22 14 0 253 displaystyle P 2 frac 1 14 14 1 left 0 2 2 2 6 2 4 2 2 2 14 right 0 253 P displaystyle bar P degerini hesaplamak icin Pi displaystyle P i toplami bulunur 1 000 0 253 0 286 0 286 3 780 displaystyle 1 000 0 253 0 286 0 286 3 780 dd Tum veri serisi ve hesaplama sayfasi icin P 1 10 14 14 1 3 780 14 14 1 0 378 displaystyle bar P frac 1 10 14 14 1 left 3 780 14 14 1 right 0 378 P e 0 1432 0 2002 0 2792 0 1502 0 2292 0 213 displaystyle bar P e 0 143 2 0 200 2 0 279 2 0 150 2 0 229 2 0 213 Sonuc olarak Kappa formulu kullanilir k 0 378 0 2131 0 213 0 210 displaystyle kappa frac 0 378 0 213 1 0 213 0 210 Sonuc yorumlamasiLandis ve Koch 1977 elde edilen k displaystyle kappa degerlerini yorumlamak icin su tabloyu sunmuslardir k displaystyle kappa Yorum lt 0 Hic uyusma olmamasi0 0 0 20 Onemsiz uyusma olmasi0 21 0 40 Orta derecede uyusma olmasi0 41 0 60 Ekseriyetle uyusma olmasi0 61 0 80 Onemli derecede uyusma olmasi0 81 1 00 Neredeyse mukemmel uyusma olmasi Verilen orneginde k 0 211 displaystyle kappa 0 211 bulundugu icin ancak orta dereceli bir uyusma oldugu sonucu cikarilabilir Ancak bu tabloda verilen yorumlar ve hatta verilen araliklar hakkinda istatistikciler arasinda anlasmazlik vardir Landis ve Koch yazilarinda verdikleri araliklar ve yorumlar icin teorik delil vermemislerdir ve bu ifadeler ancak birer sahsi inanc olarak kabul edilebilirler Bazi istatistikcilere gore bu araliklar ve yorumlar arastirmacilara zararli olabilirler Bu araliklar ve yorumlar arastiricilara Kappa degerinin degisken kategori sayisindan da yani Cden etkilendigi gercegini unutturabilir Bilinmektedir ki kategori sayisi ne kadar kucuk olursa kappa degeri de buyuk olmaktadir Icsel kaynaklarVikikitap Vikikitapta bu konu hakkinda daha fazla bilgi var Algorithm implementation Cohen in kappa katsayisi Pearson un carpim moment korelasyon katsayisiKaynakca Fleiss J L 1971 Measuring nominal scale agreement among many raters Psychological Bulletin Cilt 76 Sayi 5 say 378 382 Scott W 1955 Reliability of content analysis The case of nominal scale coding Public Opinion Quarterly Cilt 19 Sayi 3 say 321 325 Cohen J 1960 A coefficient of agreement for nominal scales Educational and Psychological Measurement Cilt 20 Sayi 1 say 37 46 Landis J R ve Koch G G 1977 The measurement of observer agreement for categorical data Biometrics Cilt 33 say 159 174 Gwet K 2001 Statistical Tables for Inter Rater Agreement Gaithersburg StatAxis Publishing Sim J and Wright C C 2005 The Kappa Statistic in Reliability Studies Use Interpretation and Sample Size Requirements in Physical Therapy Cilt 85 say 257 268Dis baglantilarKatsayi hakkinda kapsamli bir makaleler bibliyografyasi vermektedir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans

















