Foton polarizasyonu (foton kutuplanımı) klasik polarize sinüsoidal düzlem elektromanyetik dalgasının kuantum mekaniksel açıklamasıdır. Bireysel foton özdurumları ya sağ ya da sol dairesel polarizasyona sahiptir. Süperpozisyon özdurumu içinde olan bir foton lineer, dairesel veya eliptik polarizasyona sahip olabilir.
Foton polarizasyon açıklaması fiziksel kavramlar ve çok karışık kuantum tanımlarının matematiksel mekanizmaların çoğunu içerir. Potansiyel kuyusunda bulunan bir elektronun kuantum mekaniği ve daha karmaşık kuantum olaylarının temel bir esas olarak anlaşılması buna örneklerdir. Matematik mekaniğinin çoğunu oluşturan durum vektörleri, olasılık genlikleri, üniter operatörler ve Hermityen operatörleri klasik Maxwell denklemleriyle bunu ortaya çıkarır. Foton için kuantum polarizasyon durum vektörü, örneğin, genellikle klasik bir dalganın polarizasyon tanımlamak için kullanılan Jones vektörü ile aynıdır. Üniter operatörler, klasik bir dalganın medya aracılığıyla yayılmasını, bir dalganın polarizasyon durumunu değiştirerek enerji korunumunun klasik gerekliliklerini ortaya çıkarır. Sonra, Hermityen operatörler klasik polarizasyon durumunun sonsuz dönüşümlerini izler.
Matematiksel mekaniklerin gerekliliklerinin birçoğu deneysel bir yolla kolayca doğrulanabilir. Aslında, birçok deney Polaroid gözlüğün iki çifti (ya da bir kırık çift) ile yapılabilir.
Kuantum mekaniği ile bir bağlantı, elektromanyetik alanda bir enerji için foton olarak adlandırılan minimum boyun tanımlanmasıyla yapılır. Kimlik tanımlama Planck teorileri ve Einstein tarafından bu kuramların yorumlanmasına dayanmaktadır. Haberleşme ilkesi daha sonra bir foton ile, devinirlik ve açısal devinirliğin enerjisiyle birlikte tanımlanmasına olanak sağlar.
Klasik elektromanyetik dalgaların polarizasyonu
Polarizasyon durumları
Lineer polarizasyon

Faz açıları olan 
Bu, x eksenine göre 

X veya y eksenindeki lineer polarizasyon için olan durum vektörleri, bu durum vektörünün özel durumlarıdır.
Birim vektörleri şu şekilde tanımlanıyorsa;
ve
“x-y esasında” lineer olarak kutuplaşmış polarizasyon durumu şu şekilde yazılabilir;
Dairesel polarizasyon
Eğer faz açıları olan 


artı işareti sağ polarizasyonu, eksi işareti ise sol polarizasyonu gösterir. Dairesel kutuplaşma durumunda, elektrik alan vektörünün sabit büyüklüğü x-y ekseninde döner.
Birim vektörleri şu şekilde tanımlanıyorsa;
ve
"R-L esasında" gelişigüzel polarizasyon durumu şu şekilde yazılabilir;
Bu yazılımda;
ve
Bundan dolayı;
Eliptik polarizasyon
Elektrik alanı x-y düzleminde dönen ve değişken büyüklüğe sahip genel duruma eliptik polarizasyon denir. Durum vektörü şu şekilde gösterilir;
Gelişigüzel bir polarizasyon durumunun geometrik olarak görselleştirilmesi
Polarizasyon durumunun nasıl göründüğünü anlamak için polarizasyon durumu 
Yani, polarizasyon durumu yorumlanırken (x(t), y(t)) 'nin dönüş yönü ve izlediği yol dikkate alınır.
(x(t) ve y(t) yukarıda tanımlandığı gibi.) ve genel olarak daha çok sağ dairesel veya sol dairesel olup olmamasından (bu ya |ψR| > |ψL| ya da tam tersidir.), fiziksel yorumlanmasının gelişigüzel bir faz katsayısıyla çarpılsa bile aynı olacağını gösterir. Bundan dolayı,
ve dönüş yönü aynı kalır. Diğer bir deyişle, 

Bir doğrusal polarize durum için; x-y düzleminde bulunan, eğimi tan(θ) ve uzunluğu 2 birim ve orta noktası orijin olan M çizgisi görülebilir. Dairesel polarize durumu için, M yarıçapı 1/√2 olan ve orta noktası orijinde bulunan bir çember olur.
Klasik elektromanyetik bir dalganın enerjisi, devinirliği ve açısal devinirliği
Klasik elektromanyetik dalgaların enerji yoğunluğu
Düzlem dalgasının enerjisi
Klasik elektromanyetik alanların birim hacme düşen enerjisi; (cgs birim sistemine göre)
Düzlem dalgaları için bu formül;
Enerji, dalganın dalga uzunluğu üstünde ortalanmıştır.
Her bir bileşenin enerji orantısı
Düzlem dalgasının x bileşenine göre enerji orantısı;
y bileşenine göre aynı gösterim şu şekildedir; 
İki bileşenin oranı şu şekildedir:
Klasik elektromanyetik dalgaların devinirlik yoğunluğu
Devinirlik yoğunluğu Poynting vektörü ile verilmiştir.
Z yönünde hareket eden bir sinüzodial düzlem dalgası için, devinirlik z yönündedir ve enerji yoğunluğu ile ilgilidir:
Devinirlik yoğunluğu dalga uzunluğu üstünde ortalanmıştır.
Klasik elektromanyetik dalgaların açısal devinirlik yoğunlukları
Elektromanyetik dalgalar hem yörüngesel açısal devinirliğe hem de fırıl açısal devinirliğine sahip olabilir. Toplam açısal devinirlik yoğunluğu ise aşağıdaki gibidir.


Yine, yoğunluk dalga boyu üstünde ortalanmıştır.
Optik filtreler ve kristaller
Klasik bir dalganın polaroid filtreden geçişi

Bir lineer filtre bir düzlem dalganın bir bileşeni iletir ve dik bileşeni emer. Bu durumda, eğer filtre x yönünde kutuplaşırsa, filtreden geçen enerjinin oranı aşağıdaki gibidir.
Enerji korunumuna örnek: Klasik bir dalganın çift kırınımlı kristalden geçişi
İdeal bir çift kırınımlı kristal dalga enerjisinin kaybı olmadan bir elektromanyetik dalganın kutuplanım durumunu dönüştürür. Bu nedenle çift kırınımlı kristaller polarizasyon durumlarının korunumlu dönüşümünü incelemek için ideal bir test yatağı sağlar. Bu tedavi hala tamamen klasik olsa da, üniter ve Hermityen operatörler gibi standart kuantum araçları değişmiş durumu zaman içinde doğal olarak ortaya çıkarır.
Başlangıç ve bitiş durumları
Bir "optik eksene" sahip çift kırınımlı kristaller, kutuplu ışık bu optik eksene paralelken dik olduğundan daha farklı kırınım dizinlerine sahiptir. Kutuplu ışığın paralel olduğu eksene "sıra dışı ışınlar" veya "sıra dışı fotonlar", kutuplu ışığın dik olduğu eksenlere de "olağan ışınlar" veya "olağan fotonlar" denir. Eğer doğrusal kutuplaşmış dalgalar kristale çarparsa; dalganın sıra dışı bileşeni, olağan bileşeninden daha farklı bir fazda olan kristalden ortaya çıkar. Matematik dilinde, eğer çarpan dalga doğrusal olarak optik eksene göre 
ve ortaya çıkan dalganın durum vektörü şu şekilde yazılabilir;
Başlangıç durumu doğrusal olarak kutuplaşırken, son durum eliptik olarak kutuplaşır. Çift kırınımlı kristal kutuplaşma karakterini değiştirir.
Son durumun ikilisi

Başlangıç kutuplaşma durumu operatör U'yla son duruma dönüşür. Son durumun ikilisi şu şekilde gösterilir;

Bütün operatörler ve enerji korunumu
Kristalden çıkan enerji oratısı şu şekildedir;
Bu ideal durumda, bütün kristale çarpan enerjiler kristalden ortaya çıkar. U işlemcisi şu özelliğe sahiptir;
Formüldeki I kimlik operatörüdür, U ise bütün operatörüdür. Bütünlük özelliği enerji korunumunu durum dönüşümlerinde sağlamak açısından gereklidir.
Hermityan işlemcileri ve enerji korunumu

Eğer kristal çok inceyse, son durum başlangıç durumundan çok az bir farklılık gösterir. Bütün işlemcisi kimlik işlemcisini kapatır. H işlemcisi şu şekilde tanımlanabilir;
ve bitiştirilmişi şu şekildedir;
Enerji korunumu sonrasında şunu gerektirir;
Bu ise aşağıdakini gerektirir
Bitiştirilmişine eşit olan işlemcilere Hermityan ya da kendinden bitiştirilmiş denir.
Kutuplaşma durumunun mini geçişi şu şekildedir;
Bu nedenle, enerji korunumu Hermityan işlemcisinde gerçekleşen kutuplaşma durumunda mini geçiş gerektirir.
Fotonlar: Kuantum mekaniği ile bağlantı
Fotonların enerjisi, devinirliği ve açısal devinirliği
Enerji
Bu kısma kadar olan işleyiş klasik fiziğe aittir. Elektrodinamik için olan Maxwell denklemleri, klasik niceliklerin tekrar yorumlanmasıyla kuantum mekaniğine uygulanabilir. Bu tekrar yorumlama Max Planck'in teorilerini baz alarak ve Albert Einstein'ın yorumlamalarını göz önünde bulundurarak olabilir.
Einstein ışılelektrik etkisiyle ilgili ilk deneylerini, elektromanyetik radyasyonun indirgenemez enerji paketlerinden oluştuğunu ve bu enerji paketlerini foton (ışıl) olarak tanımlayarak sonuçlandırmıştır. Her bir paketteki enerji dalganın açısal frekansıyla ilişkilidir. Bu ilişki aşağıdaki gibidir.
Bu denklemdeki 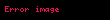


ve enerji yoğunluğu;
Bir fotonun enerjisi haberleşme prensibince klasik alanlarla ilgilidir. Haberleşme prensibi çok sayıda foton için kuantum ve klasik fizik yasalarının uymasını gerektirir. Bu nedenle, çok sayıda 
Öyleyse, kutu içindeki fotonların sayısı;
Devinirlik
Haberleşme yasası ayrıca bir fotonun devinirlik ve açısal devinirliğini belirler. Devinirlik için;
Bu denklemde kz dalga numarasıdır. Bu bir fotonun devinirliğini şu şekilde belirtir;
Açısal devinirlik ve fırıl
Fırıl açısal momentumunda da olduğu gibi;
Bu formülde Ec alan gücünü gösterir. Bu denklemden, bir fotonun fırıl açısal devinirliği şu şekilde açıklanır;
Fırıl işlemcisi
Fotonun fırılı, fırıl açısal devinirlik hesaplamalarında 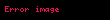


Bir fırıl işlemcisinin özvektörleri 

Bir fotonun fırıl ölçümlerinin beklenen değeri şu şekildedir;
İşlemci S gözlenebilir bir nicelik olan fırıl açısal devinirliği ile ilişkilidir. İşlemcinin özdeğerleri gözlenebilir değerlerin bulunmasına yardımcı olur. Bu fırıl açısal momentum için gösterilmiştir fakat genellikle her gözlenebilir nicelik için doğrudur.
Fırıl durumları
Dairesel kutuplaşma durumları şu şekilde yazılabilir;
Bu denklemdeki s=1
ve bu denklemde s= -1
Rastgele durum şu şekilde yazılabilir;
Bu denklem için;
Diferansiyel biçimde fırıl ve açısal momentum işlemcileri
Durum fırıl belirtkesinde yazıldığında, fırıl işlemcisi şu şekilde yazılır;
Diferansiyel fırıl işlemcisinin özvektörleri şu şekildedir:
ve
Fırıl açısal momentum işlemcisi ise şu şekildedir:
Kuantum mekaniğinde olasılığın doğası
Tek foton için olasılık
Olasılığın fotonların davranışlarına uygulanabildiği iki yol vardır; olasılık belirli bir durumdaki muhtemel sayıda fotonları hesaplamada kullanılabilir ya da belirli bir durumdaki tek bir fotonun olasılığını hesaplamada kullanılabilir. Eski yorumlama enerji yasasını ihlal ediyordu. Sonraki yorumlamalar ise eğer seçenek sezgisel değilse geçerlidir. Dirac bunu çift-yarık deneylerinin içeriğinde açıklamıştır.
Olasılık genlikleri
Belirli bir kutuplaşma halinde olan bir foton için olasılık klasik Maxwell denklemleri ile hesaplanabilir. Fotonun kutuplaşma durumu alanı ile orantılıdır. Olasılığın kendisi alanlarda ikinci derecedendir ve buna bağlı olarak da kutuplaşma kuantum halinde ikinci derecedendir. Kuantum mekaniğinde, bu nedenle, durum ya da olasılık genliği temel olasılık bilgileri içerir. Genel olarak, olasılık genliklerinin birleştirilmesi için olan kurallar klasik kurallardakine çok benzerdir.
Belirsizlik prensibi

 Bu;
Bu; 
'dır.
Matematiksel hazırlık
Herhangi bir resmi işlemci için Cauchy-Schwarz eşitsizliğinin sonucu olan aşağıdaki eşitsizlik doğrudur.
Eğer B A ψ ve A B ψ tanımlanırsa;
bu denklemde;
ve
Bu
A ve B'nin çeviricisi olarak adlandırılır.
Bu tamamiyle matematiksel bir sonuçtur. Hiçbir fiziksel nicelik veya yasayla ilgisi yoktur. Bu sadece durum üzerine etki eden bir işlemcinin belirsizliğinin başka bir işlemcinin belirsizliğiyle çarpımının illaki sıfır olmamasını gösterir.
Açısal devinimin uygulaması
Eğer işlemciyi açısal devinim ve kutuplaşma açısıyla tanımlarsak fizik ile ilişkisini bulabiliriz:
bu basitçe açısal devinim ve kutuplaşma açısının sınırsız kesinlik ile eşzamanlı olarak ölçülemeyeceğini gösterir.
Durumlar, olasılık genlikleri, bütün ve Hermityan işlemciler ve özvektörler
Kuantum mekaniğinin birçok matematiksel aygıtı, kutuplaşmış bir sinüzoidal elektromanyetik dalganın klasik açıklamasında da görünür. Klasik bir dalga için Jones vektör, örneğin, bir foton için kuantum kutuplaşma durum vektörü ile aynıdır. Jones vektörünün sağ ve sol dairesel bileşenleri fotonun fırıl hallerinin olasılık genlikleri olarak yorumlanabilir. Enerji korunumu durumların üniter işlemciyle donüşmesini gerektirir. Bu, son derece küçük dönüşümler Hermityen işlemcileriyle dönüşenilir demektir. Bu sonuçlar, klasik dalgalar için Maxwell denklemlerinin yapısının doğal bir sonucu olduğunu gösterir.
Gözlenen nicelikler ölçüldüğünde ve sürekli olmak yerine ayrık olduğunda, kuantum mekaniği devreye girer. Izin verilen gözlemlenebilir değerleri işlemcilerin özdeğerlerinin gözlenebilirle ilişkisinde bulunabilir. Açısal devinim durumunda, örneğin, izin verilen gözlemlenebilir değerler spin işlemcisinin özdeğerleridir.
Bu kavramlar Maxwell denklemleri ve Planck ile Einstein'ın teorilerinden ortaya çıkmıştır ve başka fizik sistemlerinde de doğru bulunmuşlardır. Aslında, tipik program, bu bölümün kavramlarını varsaymak ve daha sonra fiziksel bir sistemin bilinmeyen dinamiklerini anlaması içindir. Bu, elektron hareketliliği için uygulandı. Bu durumda, bu bölümdeki esaslara tekrar baktığımızda, Schrödinger'in denklemine katkıda bulunduğunu görürüz. Atomlar için bu denklemin çözümü, atom spektrumları için Balmer serisine açıklama getirdi ve dolayısıyla atom fiziği ve kimya için birer temel oluşturmuş oldu.
Bu Maxwell denklemlerinin Newton mekaniğinin yeniden bir yapılandırmaya zorlamasının tek nedeni değildir. Maxwell denklemleri izafi olarak tutarlıdır. Özel görelilik Maxwell denklemlerinin klasik mekaniği tutarlı yapmak için girdiği girişimlerin sonucudur.
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Foton polarizasyonu foton kutuplanimi klasik polarize sinusoidal duzlem elektromanyetik dalgasinin kuantum mekaniksel aciklamasidir Bireysel foton ozdurumlari ya sag ya da sol dairesel polarizasyona sahiptir Superpozisyon ozdurumu icinde olan bir foton lineer dairesel veya eliptik polarizasyona sahip olabilir Foton polarizasyon aciklamasi fiziksel kavramlar ve cok karisik kuantum tanimlarinin matematiksel mekanizmalarin cogunu icerir Potansiyel kuyusunda bulunan bir elektronun kuantum mekanigi ve daha karmasik kuantum olaylarinin temel bir esas olarak anlasilmasi buna orneklerdir Matematik mekaniginin cogunu olusturan durum vektorleri olasilik genlikleri uniter operatorler ve Hermityen operatorleri klasik Maxwell denklemleriyle bunu ortaya cikarir Foton icin kuantum polarizasyon durum vektoru ornegin genellikle klasik bir dalganin polarizasyon tanimlamak icin kullanilan Jones vektoru ile aynidir Uniter operatorler klasik bir dalganin medya araciligiyla yayilmasini bir dalganin polarizasyon durumunu degistirerek enerji korunumunun klasik gerekliliklerini ortaya cikarir Sonra Hermityen operatorler klasik polarizasyon durumunun sonsuz donusumlerini izler Matematiksel mekaniklerin gerekliliklerinin bircogu deneysel bir yolla kolayca dogrulanabilir Aslinda bircok deney Polaroid gozlugun iki cifti ya da bir kirik cift ile yapilabilir Kuantum mekanigi ile bir baglanti elektromanyetik alanda bir enerji icin foton olarak adlandirilan minimum boyun tanimlanmasiyla yapilir Kimlik tanimlama Planck teorileri ve Einstein tarafindan bu kuramlarin yorumlanmasina dayanmaktadir Haberlesme ilkesi daha sonra bir foton ile devinirlik ve acisal devinirligin enerjisiyle birlikte tanimlanmasina olanak saglar Klasik elektromanyetik dalgalarin polarizasyonuPolarizasyon durumlari Lineer polarizasyon Polarizenin camur duzluklerinden yansimasina etkisi Ilk resimde polarize etkisini en aza indirmek icin dondurulur ikinci resimde onu maksimize etmek icin 90 dondurulur hemen hemen tum yansiyan gunes isigi elimine edilir Faz acilari olan axveay displaystyle alpha x ve alpha y esitken dalga lineer olarak ya da duzlem olarak kutuplasmistir ax ay def a displaystyle alpha x alpha y stackrel mathrm def alpha Bu x eksenine gore a displaystyle alpha fazinda bir dalganin 8 displaystyle theta acisiyla kutuplasmis oldugunu gosterir Bu durumda Jones vektoru su sekilde yazilir ps cos 8sin 8 exp ia displaystyle psi rangle begin pmatrix cos theta sin theta end pmatrix exp left i alpha right X veya y eksenindeki lineer polarizasyon icin olan durum vektorleri bu durum vektorunun ozel durumlaridir Birim vektorleri su sekilde tanimlaniyorsa x def 10 displaystyle x rangle stackrel mathrm def begin pmatrix 1 0 end pmatrix ve y def 01 displaystyle y rangle stackrel mathrm def begin pmatrix 0 1 end pmatrix x y esasinda lineer olarak kutuplasmis polarizasyon durumu su sekilde yazilabilir ps cos 8exp ia x sin 8exp ia y psx x psy y displaystyle psi rangle cos theta exp left i alpha right x rangle sin theta exp left i alpha right y rangle psi x x rangle psi y y rangle Dairesel polarizasyon Eger faz acilari olan ax displaystyle alpha x ve ay displaystyle alpha y birbirlerinden tam olarak p 2 displaystyle pi 2 kadar farklilarsa ve x in genligi y nin genligine esitse bu dalga dairesel olarak kutuplasmistir Bu durumda Jones vektoru ps 12 1 i exp iax displaystyle psi rangle frac 1 sqrt 2 begin pmatrix 1 pm i end pmatrix exp left i alpha x right arti isareti sag polarizasyonu eksi isareti ise sol polarizasyonu gosterir Dairesel kutuplasma durumunda elektrik alan vektorunun sabit buyuklugu x y ekseninde doner Birim vektorleri su sekilde tanimlaniyorsa R def 12 1i displaystyle R rangle stackrel mathrm def 1 over sqrt 2 begin pmatrix 1 i end pmatrix ve L def 12 1 i displaystyle L rangle stackrel mathrm def 1 over sqrt 2 begin pmatrix 1 i end pmatrix R L esasinda gelisiguzel polarizasyon durumu su sekilde yazilabilir ps psR R psL L displaystyle psi rangle psi R R rangle psi L L rangle Bu yazilimda psR R ps 12 cos 8exp iax isin 8exp iay displaystyle psi R langle R psi rangle frac 1 sqrt 2 cos theta exp i alpha x i sin theta exp i alpha y ve psL L ps 12 cos 8exp iax isin 8exp iay displaystyle psi L langle L psi rangle frac 1 sqrt 2 cos theta exp i alpha x i sin theta exp i alpha y Bundan dolayi 1 psR 2 psL 2 displaystyle 1 psi R 2 psi L 2 Eliptik polarizasyon Elektrik alani x y duzleminde donen ve degisken buyukluge sahip genel duruma eliptik polarizasyon denir Durum vektoru su sekilde gosterilir ps def psxpsy cos 8exp iax sin 8exp iay displaystyle psi rangle stackrel mathrm def begin pmatrix psi x psi y end pmatrix begin pmatrix cos theta exp left i alpha x right sin theta exp left i alpha y right end pmatrix Gelisiguzel bir polarizasyon durumunun geometrik olarak gorsellestirilmesi Polarizasyon durumunun nasil gorundugunu anlamak icin polarizasyon durumu eiwt displaystyle e i omega t faz katsayisiyla carpilan yorungesi incelenebilir ve sonra reel kisimlari x ve y koordinatlarina gore yorumlanabilir Bu durum su sekilde gosterilebilir x t y t ℜ eiwtpsx ℜ eiwtpsy ℜ eiwt psxpsy ℜ eiwt ps displaystyle begin pmatrix x t y t end pmatrix begin pmatrix Re e i omega t psi x Re e i omega t psi y end pmatrix Re left e i omega t begin pmatrix psi x psi y end pmatrix right Re left e i omega t psi rangle right Yani polarizasyon durumu yorumlanirken x t y t nin donus yonu ve izledigi yol dikkate alinir M ps x t y t t displaystyle M psi rangle left left Big x t y t Big right forall t right x t ve y t yukarida tanimlandigi gibi ve genel olarak daha cok sag dairesel veya sol dairesel olup olmamasindan bu ya ps R gt ps L ya da tam tersidir fiziksel yorumlanmasinin gelisiguzel bir faz katsayisiyla carpilsa bile ayni olacagini gosterir Bundan dolayi M eia ps M ps a R displaystyle M e i alpha psi rangle M psi rangle alpha in mathbb R ve donus yonu ayni kalir Diger bir deyisle ps displaystyle psi rangle ve eia ps displaystyle e i alpha psi rangle polarizasyonlari arasinda faz katsayisi disinda fiziksel bir farklilik yoktur Bir dogrusal polarize durum icin x y duzleminde bulunan egimi tan 8 ve uzunlugu 2 birim ve orta noktasi orijin olan M cizgisi gorulebilir Dairesel polarize durumu icin M yaricapi 1 2 olan ve orta noktasi orijinde bulunan bir cember olur Klasik elektromanyetik bir dalganin enerjisi devinirligi ve acisal devinirligiKlasik elektromanyetik dalgalarin enerji yogunlugu Duzlem dalgasinin enerjisi Klasik elektromanyetik alanlarin birim hacme dusen enerjisi cgs birim sistemine gore Ec 18p E2 r t B2 r t displaystyle mathcal E c frac 1 8 pi left mathbf E 2 mathbf r t mathbf B 2 mathbf r t right Duzlem dalgalari icin bu formul Ec E 28p displaystyle mathcal E c frac mid mathbf E mid 2 8 pi Enerji dalganin dalga uzunlugu ustunde ortalanmistir Her bir bilesenin enerji orantisi Duzlem dalgasinin x bilesenine gore enerji orantisi fx E 2cos2 8 E 2 psx psx cos2 8 displaystyle f x frac mid mathbf E mid 2 cos 2 theta mid mathbf E mid 2 psi x psi x cos 2 theta y bilesenine gore ayni gosterim su sekildedir fy sin2 8 displaystyle f y sin 2 theta Iki bilesenin orani su sekildedir psx psx psy psy ps ps 1 displaystyle psi x psi x psi y psi y langle psi psi rangle 1 Klasik elektromanyetik dalgalarin devinirlik yogunlugu Devinirlik yogunlugu Poynting vektoru ile verilmistir P 14pcE r t B r t displaystyle boldsymbol mathcal P 1 over 4 pi c mathbf E mathbf r t times mathbf B mathbf r t Z yonunde hareket eden bir sinuzodial duzlem dalgasi icin devinirlik z yonundedir ve enerji yogunlugu ile ilgilidir Pzc Ec displaystyle mathcal P z c mathcal E c Devinirlik yogunlugu dalga uzunlugu ustunde ortalanmistir Klasik elektromanyetik dalgalarin acisal devinirlik yogunluklari Elektromanyetik dalgalar hem yorungesel acisal devinirlige hem de firil acisal devinirligine sahip olabilir Toplam acisal devinirlik yogunlugu ise asagidaki gibidir L r P 14pcr E r t B r t displaystyle boldsymbol mathcal L mathbf r times boldsymbol mathcal P 1 over 4 pi c mathbf r times left mathbf E mathbf r t times mathbf B mathbf r t right Z displaystyle Z ekseni boyunca yayilan sinuzoidal duzlem dalgasinin acisal devinirlik yogunlugu kaybolur Firil acisal devinirlik yogunlugu z displaystyle z eksenindedir ve su sekildedir L E 28pw R ps 2 L ps 2 1wEc psR 2 psL 2 displaystyle mathcal L mid mathbf E mid 2 over 8 pi omega left mid langle R psi rangle mid 2 mid langle L psi rangle mid 2 right 1 over omega mathcal E c left mid psi R mid 2 mid psi L mid 2 right Yine yogunluk dalga boyu ustunde ortalanmistir Optik filtreler ve kristallerKlasik bir dalganin polaroid filtreden gecisi Dogrusal Kutuplasma Bir lineer filtre bir duzlem dalganin bir bileseni iletir ve dik bileseni emer Bu durumda eger filtre x yonunde kutuplasirsa filtreden gecen enerjinin orani asagidaki gibidir fx psx psx cos2 8 displaystyle f x psi x psi x cos 2 theta Enerji korunumuna ornek Klasik bir dalganin cift kirinimli kristalden gecisi Ideal bir cift kirinimli kristal dalga enerjisinin kaybi olmadan bir elektromanyetik dalganin kutuplanim durumunu donusturur Bu nedenle cift kirinimli kristaller polarizasyon durumlarinin korunumlu donusumunu incelemek icin ideal bir test yatagi saglar Bu tedavi hala tamamen klasik olsa da uniter ve Hermityen operatorler gibi standart kuantum araclari degismis durumu zaman icinde dogal olarak ortaya cikarir Baslangic ve bitis durumlari Bir optik eksene sahip cift kirinimli kristaller kutuplu isik bu optik eksene paralelken dik oldugundan daha farkli kirinim dizinlerine sahiptir Kutuplu isigin paralel oldugu eksene sira disi isinlar veya sira disi fotonlar kutuplu isigin dik oldugu eksenlere de olagan isinlar veya olagan fotonlar denir Eger dogrusal kutuplasmis dalgalar kristale carparsa dalganin sira disi bileseni olagan bileseninden daha farkli bir fazda olan kristalden ortaya cikar Matematik dilinde eger carpan dalga dogrusal olarak optik eksene gore 8 displaystyle theta acisiyla kutuplasmissa carpma durum vektoru su sekilde yazilabilir ps cos 8sin 8 displaystyle psi rangle begin pmatrix cos theta sin theta end pmatrix ve ortaya cikan dalganin durum vektoru su sekilde yazilabilir ps cos 8exp iax sin 8exp iay exp iax 00exp iay cos 8sin 8 def U ps displaystyle psi rangle begin pmatrix cos theta exp left i alpha x right sin theta exp left i alpha y right end pmatrix begin pmatrix exp left i alpha x right amp 0 0 amp exp left i alpha y right end pmatrix begin pmatrix cos theta sin theta end pmatrix stackrel mathrm def hat U psi rangle Baslangic durumu dogrusal olarak kutuplasirken son durum eliptik olarak kutuplasir Cift kirinimli kristal kutuplasma karakterini degistirir Son durumun ikilisi Cift kirilmayi gostermek icin yazili bir kagit uzerinde bulunan kalsit kristali Baslangic kutuplasma durumu operator U yla son duruma donusur Son durumun ikilisi su sekilde gosterilir ps ps U displaystyle langle psi langle psi hat U dagger U displaystyle U dagger U nun bitistirilmisidir yani matrisin karmasik eslenik devrigidir Butun operatorler ve enerji korunumu Kristalden cikan enerji oratisi su sekildedir ps ps ps U U ps ps ps 1 displaystyle langle psi psi rangle langle psi hat U dagger hat U psi rangle langle psi psi rangle 1 Bu ideal durumda butun kristale carpan enerjiler kristalden ortaya cikar U islemcisi su ozellige sahiptir U U I displaystyle hat U dagger hat U I Formuldeki I kimlik operatorudur U ise butun operatorudur Butunluk ozelligi enerji korunumunu durum donusumlerinde saglamak acisindan gereklidir Hermityan islemcileri ve enerji korunumu Dixon New Mexico dan cifter yansilamli Kalsit Bu kristal 16 kilogram agirligindadir ve National Museum of Natural History de sergilenmektedir Eger kristal cok inceyse son durum baslangic durumundan cok az bir farklilik gosterir Butun islemcisi kimlik islemcisini kapatir H islemcisi su sekilde tanimlanabilir U I iH displaystyle hat U approx I i hat H ve bitistirilmisi su sekildedir U I iH displaystyle hat U dagger approx I i hat H dagger Enerji korunumu sonrasinda sunu gerektirir I U U I iH I iH I iH iH displaystyle I hat U dagger hat U approx left I i hat H dagger right left I i hat H right approx I i hat H dagger i hat H Bu ise asagidakini gerektirir H H displaystyle hat H hat H dagger Bitistirilmisine esit olan islemcilere Hermityan ya da kendinden bitistirilmis denir Kutuplasma durumunun mini gecisi su sekildedir ps ps iH ps displaystyle psi rangle psi rangle i hat H psi rangle Bu nedenle enerji korunumu Hermityan islemcisinde gerceklesen kutuplasma durumunda mini gecis gerektirir Fotonlar Kuantum mekanigi ile baglantiFotonlarin enerjisi devinirligi ve acisal devinirligi Enerji Bu kisma kadar olan isleyis klasik fizige aittir Elektrodinamik icin olan Maxwell denklemleri klasik niceliklerin tekrar yorumlanmasiyla kuantum mekanigine uygulanabilir Bu tekrar yorumlama Max Planck in teorilerini baz alarak ve Albert Einstein in yorumlamalarini goz onunde bulundurarak olabilir Einstein isilelektrik etkisiyle ilgili ilk deneylerini elektromanyetik radyasyonun indirgenemez enerji paketlerinden olustugunu ve bu enerji paketlerini foton isil olarak tanimlayarak sonuclandirmistir Her bir paketteki enerji dalganin acisal frekansiyla iliskilidir Bu iliski asagidaki gibidir ϵ ℏw displaystyle epsilon hbar omega Bu denklemdeki ℏ displaystyle hbar Planck sabiti olarak tanimlanmistir Eger N displaystyle N adet foton V displaystyle V hacminde bulunuyorsa elektromanyetik alandaki enerji Nℏw displaystyle N hbar omega ve enerji yogunlugu NℏwV displaystyle N hbar omega over V Bir fotonun enerjisi haberlesme prensibince klasik alanlarla ilgilidir Haberlesme prensibi cok sayida foton icin kuantum ve klasik fizik yasalarinin uymasini gerektirir Bu nedenle cok sayida N displaystyle N icin kuantum enerji yogunlugu ve klasik enerji yogunlugu ayni olmalidir NℏwV Ec E 28p displaystyle N hbar omega over V mathcal E c frac mid mathbf E mid 2 8 pi Oyleyse kutu icindeki fotonlarin sayisi N V8pℏw E 2 displaystyle N frac V 8 pi hbar omega mid mathbf E mid 2 Devinirlik Haberlesme yasasi ayrica bir fotonun devinirlik ve acisal devinirligini belirler Devinirlik icin Pz NℏwcV NℏkzV displaystyle mathcal P z N hbar omega over cV N hbar k z over V Bu denklemde kz dalga numarasidir Bu bir fotonun devinirligini su sekilde belirtir pz ℏkz displaystyle p z hbar k z Acisal devinirlik ve firil Firil acisal momentumunda da oldugu gibi L 1wEc psR 2 psL 2 NℏV psR 2 psL 2 displaystyle mathcal L 1 over omega mathcal E c left mid psi R mid 2 mid psi L mid 2 right N hbar over V left mid psi R mid 2 mid psi L mid 2 right Bu formulde Ec alan gucunu gosterir Bu denklemden bir fotonun firil acisal devinirligi su sekilde aciklanir lz ℏ psR 2 psL 2 displaystyle l z hbar left mid psi R mid 2 mid psi L mid 2 right Firil islemcisi Fotonun firili firil acisal devinirlik hesaplamalarinda ℏ displaystyle hbar in katsayisi olarak tanimlanmistir Eger bir foton R displaystyle R rangle durumunda ise bu fotonun firili 1dir ve bu foton L displaystyle L rangle durumunda ise firili 1dir Firil islemcisi dis carpim olarak tanimlanmistir S def R R L L 0 ii0 displaystyle hat S stackrel mathrm def R rangle langle R L rangle langle L begin pmatrix 0 amp i i amp 0 end pmatrix Bir firil islemcisinin ozvektorleri R displaystyle R rangle ve L displaystyle L rangle dir ve sirasiyla ozdegerleri 1 ve 1dir Bir fotonun firil olcumlerinin beklenen degeri su sekildedir ps S ps psR 2 psL 2 displaystyle langle psi hat S psi rangle mid psi R mid 2 mid psi L mid 2 Islemci S gozlenebilir bir nicelik olan firil acisal devinirligi ile iliskilidir Islemcinin ozdegerleri gozlenebilir degerlerin bulunmasina yardimci olur Bu firil acisal momentum icin gosterilmistir fakat genellikle her gozlenebilir nicelik icin dogrudur Firil durumlari Dairesel kutuplasma durumlari su sekilde yazilabilir s displaystyle s rangle Bu denklemdeki s 1 R displaystyle R rangle ve bu denklemde s 1 L displaystyle L rangle Rastgele durum su sekilde yazilabilir ps s 1 1asexp iax is8 s displaystyle psi rangle sum s 1 1 a s exp left i alpha x is theta right s rangle Bu denklem icin s 1 1 as 2 1 displaystyle sum s 1 1 mid a s mid 2 1 Diferansiyel bicimde firil ve acisal momentum islemcileri Durum firil belirtkesinde yazildiginda firil islemcisi su sekilde yazilir S d i 8 displaystyle hat S d rightarrow i partial over partial theta S d i 8 displaystyle hat S d dagger rightarrow i partial over partial theta Diferansiyel firil islemcisinin ozvektorleri su sekildedir exp iax is8 s displaystyle exp left i alpha x is theta right s rangle ve S dexp iax is8 s i 8exp iax is8 s s exp iax is8 s displaystyle hat S d exp left i alpha x is theta right s rangle rightarrow i partial over partial theta exp left i alpha x is theta right s rangle s left exp left i alpha x is theta right s rangle right Firil acisal momentum islemcisi ise su sekildedir l z ℏS d displaystyle hat l z hbar hat S d Kuantum mekaniginde olasiligin dogasi Tek foton icin olasilik Olasiligin fotonlarin davranislarina uygulanabildigi iki yol vardir olasilik belirli bir durumdaki muhtemel sayida fotonlari hesaplamada kullanilabilir ya da belirli bir durumdaki tek bir fotonun olasiligini hesaplamada kullanilabilir Eski yorumlama enerji yasasini ihlal ediyordu Sonraki yorumlamalar ise eger secenek sezgisel degilse gecerlidir Dirac bunu cift yarik deneylerinin iceriginde aciklamistir Olasilik genlikleri Belirli bir kutuplasma halinde olan bir foton icin olasilik klasik Maxwell denklemleri ile hesaplanabilir Fotonun kutuplasma durumu alani ile orantilidir Olasiligin kendisi alanlarda ikinci derecedendir ve buna bagli olarak da kutuplasma kuantum halinde ikinci derecedendir Kuantum mekaniginde bu nedenle durum ya da olasilik genligi temel olasilik bilgileri icerir Genel olarak olasilik genliklerinin birlestirilmesi icin olan kurallar klasik kurallardakine cok benzerdir Belirsizlik prensibi Oklit duzleminde Cauchy Schwarz esitsizligi V W V W cos a displaystyle mathbf V cdot mathbf W mathbf V mathbf W cos a Bu V W V W displaystyle mathbf V cdot mathbf W leq mathbf V mathbf W dir Matematiksel hazirlik Herhangi bir resmi islemci icin Cauchy Schwarz esitsizliginin sonucu olan asagidaki esitsizlik dogrudur 14 A B B A x x 2 A x 2 B x 2 displaystyle frac 1 4 langle hat A hat B hat B hat A x x rangle 2 leq hat A x 2 hat B x 2 Eger B A ps ve A B ps tanimlanirsa DpsA DpsB 12 A B ps displaystyle Delta psi hat A Delta psi hat B geq frac 1 2 left left langle left hat A hat B right right rangle psi right bu denklemde X ps ps X ps displaystyle left langle hat X right rangle psi left langle psi hat X psi right rangle ve DpsX X 2 ps X ps2 displaystyle Delta psi hat X sqrt langle hat X 2 rangle psi langle hat X rangle psi 2 Bu A B def A B B A displaystyle left hat A hat B right stackrel mathrm def hat A hat B hat B hat A A ve B nin ceviricisi olarak adlandirilir Bu tamamiyle matematiksel bir sonuctur Hicbir fiziksel nicelik veya yasayla ilgisi yoktur Bu sadece durum uzerine etki eden bir islemcinin belirsizliginin baska bir islemcinin belirsizligiyle carpiminin illaki sifir olmamasini gosterir Acisal devinimin uygulamasi Eger islemciyi acisal devinim ve kutuplasma acisiyla tanimlarsak fizik ile iliskisini bulabiliriz Dpsl zDps8 ℏ2 displaystyle Delta psi hat l z Delta psi theta geq frac hbar 2 bu basitce acisal devinim ve kutuplasma acisinin sinirsiz kesinlik ile eszamanli olarak olculemeyecegini gosterir Durumlar olasilik genlikleri butun ve Hermityan islemciler ve ozvektorler Kuantum mekaniginin bircok matematiksel aygiti kutuplasmis bir sinuzoidal elektromanyetik dalganin klasik aciklamasinda da gorunur Klasik bir dalga icin Jones vektor ornegin bir foton icin kuantum kutuplasma durum vektoru ile aynidir Jones vektorunun sag ve sol dairesel bilesenleri fotonun firil hallerinin olasilik genlikleri olarak yorumlanabilir Enerji korunumu durumlarin uniter islemciyle donusmesini gerektirir Bu son derece kucuk donusumler Hermityen islemcileriyle donusenilir demektir Bu sonuclar klasik dalgalar icin Maxwell denklemlerinin yapisinin dogal bir sonucu oldugunu gosterir Gozlenen nicelikler olculdugunde ve surekli olmak yerine ayrik oldugunda kuantum mekanigi devreye girer Izin verilen gozlemlenebilir degerleri islemcilerin ozdegerlerinin gozlenebilirle iliskisinde bulunabilir Acisal devinim durumunda ornegin izin verilen gozlemlenebilir degerler spin islemcisinin ozdegerleridir Bu kavramlar Maxwell denklemleri ve Planck ile Einstein in teorilerinden ortaya cikmistir ve baska fizik sistemlerinde de dogru bulunmuslardir Aslinda tipik program bu bolumun kavramlarini varsaymak ve daha sonra fiziksel bir sistemin bilinmeyen dinamiklerini anlamasi icindir Bu elektron hareketliligi icin uygulandi Bu durumda bu bolumdeki esaslara tekrar baktigimizda Schrodinger in denklemine katkida bulundugunu goruruz Atomlar icin bu denklemin cozumu atom spektrumlari icin Balmer serisine aciklama getirdi ve dolayisiyla atom fizigi ve kimya icin birer temel olusturmus oldu Bu Maxwell denklemlerinin Newton mekaniginin yeniden bir yapilandirmaya zorlamasinin tek nedeni degildir Maxwell denklemleri izafi olarak tutarlidir Ozel gorelilik Maxwell denklemlerinin klasik mekanigi tutarli yapmak icin girdigi girisimlerin sonucudur Kaynakca
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans