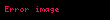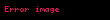Matematiğin bir alt dalı olan olasılık teorisinde (daha özelde stokastik süreçlerde) Girsanov teoremi, stokastik süreçlerin altında nasıl değiştiğini gösteren ve özellikle matematiksel finansta yaygın uygulaması olan bir teoremdir. Teorem, matematiksel finansta bir (bir hisse senedi fiyatı veya faiz oranı gibi) fiziksel ya da gözlemlenen bir ölçüde yazılan fiyat sürecinin nasıl dönüştürüleceğini gösterir. Teorem, stokastik diferansiyel denklemlerin zayıf çözümlerinin varlığını ve biricikliğini kanıtlamakta da yararlıdır.
Teoremin ifadesi







- ,
- ve aşağıdaki şartları sağlayan bir süreç olsun.
Bu koşullar altında
iyi tanımlıdır.
Girsanov teoremi,eğer 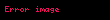
tanımının yeni bir olasılık ölçüsü verdiğini ve sabit alınmış bir 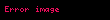
biçiminde tanımlanan 
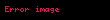

Bu teoremin ifadesi değişik kaynaklarda basitleşirilmiş ya da değişik kriterleri sağlayan halleriyle sunulabilir.
Yukarıda verilen 

koşulu sağlanıyorsa, o zaman 
Finans başta olmak üzere birçok durumda, teoremdeki 
halinde çıkar. Bu biçimdeki bir 
olmasıdır. Bu durumda, 

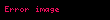
Finansta kullanımı
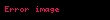



olsun.
Her 


için, 




Notlar
- ^ Karatzas & Shreve 1991, s. 302'ye bakınız.
- ^
ifadesinin aslında
ifadesi olduğu gözden kaçmamalıdır. Burada,
Doléans-Dade üsteli notasyonudur.
- ^ Karatzas & Shreve 1991, s. 191'e bakınız.
- ^ Mesela, Oksendal 2003, s. 155'ten başlayarak değişik varsayimlar altında bu teoremin üç değişik versiyonu sunulmuştur.
Kaynakça
- Karatzas, Ioannis; (1991), Brownian Motion and Stochastic Calculus, 2nd, Springer-Verlag, ISBN
- (2003). Stochastic Differential Equations: An Introduction with Applications. Springer, Berlin. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan olasilik teorisinde daha ozelde stokastik sureclerde Girsanov teoremi stokastik sureclerin altinda nasil degistigini gosteren ve ozellikle matematiksel finansta yaygin uygulamasi olan bir teoremdir Teorem matematiksel finansta bir bir hisse senedi fiyati veya faiz orani gibi fiziksel ya da gozlemlenen bir olcude yazilan fiyat surecinin nasil donusturulecegini gosterir Teorem stokastik diferansiyel denklemlerin zayif cozumlerinin varligini ve biricikligini kanitlamakta da yararlidir Teoremin ifadesi W F P displaystyle Omega mathcal F mathbb P bir olasilik uzayi Ft t 0 displaystyle mathcal F t t geq 0 bu uzayin olagan kosullari saglayan bir filtreleme ve W Wt Wt 1 Wt d Ft 0 t lt displaystyle W W t W t 1 cdots W t d mathcal F t 0 leq t lt infty P W0 0 1 displaystyle mathbb P W 0 0 1 ozelligini saglayan d displaystyle d boyutlu Brown hareketi olsun d displaystyle d boyutlu X Xt Xt 1 Xt d Ft 0 t lt displaystyle X X t X t 1 cdots X t d mathcal F t 0 leq t lt infty sureci ve asagidaki sartlari saglayan bir surec olsun P 0T Xt i 2dt lt 1 i 1 d 0 T lt displaystyle mathbb P left int 0 T X t i 2 dt lt infty right 1 quad i 1 cdots d quad 0 leq T lt infty dd Bu kosullar altinda Zt X e i 1d 0tXs i dWs i 12 0tE Xt2 ds displaystyle displaystyle Z t X e sum i 1 d int 0 t X s i dW s i frac 1 2 int 0 t E X t 2 ds iyi tanimlidir Girsanov teoremi eger Zt X displaystyle Z t X sureci martingalse P A E 1AZT X A FT displaystyle mathbb tilde P A E 1 A Z T X quad forall A in mathcal F T taniminin yeni bir olasilik olcusu verdigini ve sabit alinmis bir T 0 displaystyle T in 0 infty degeri icin W t i Wt i 0t Xs i dsi 1 d 0 t lt displaystyle tilde W t i W t i int 0 t X s i ds quad i 1 cdots d quad 0 leq t lt infty dd biciminde tanimlanan W t W t 1 W t d Ft 0 t T displaystyle tilde W t tilde W t 1 cdots tilde W t d mathcal F t 0 leq t leq T surecinin W F P displaystyle Omega mathcal F mathbb tilde P olasilik uzayinda d displaystyle d boyutlu Brown hareketi oldugunu soyler Bu teoremin ifadesi degisik kaynaklarda basitlesirilmis ya da degisik kriterleri saglayan halleriyle sunulabilir Yukarida verilen d displaystyle d boyutlu X Xt Xt 1 Xt d Ft 0 t lt displaystyle X X t X t 1 cdots X t d mathcal F t 0 leq t lt infty sureci icin E e12 0TE Xs2 ds lt 0 T lt displaystyle E left e frac 1 2 int 0 T E X s 2 ds right lt infty quad 0 leq T lt infty kosulu saglaniyorsa o zaman X displaystyle X bir martingal olur ve Girsanov teoreminin sarti saglanmis olur Bu kosula Novikov kriteri ya da Novikov kosulu denir Finans basta olmak uzere bircok durumda teoremdeki X displaystyle X sureci karsimiza Xt 0tYsdWs displaystyle X t int 0 t Y s dW s halinde cikar Bu bicimdeki bir X displaystyle X surecinin martingale olmasi icin yeterli ve gerekli kosul Novikov kosulunun saglanmasidir yani E e12 0TYs2ds lt displaystyle E left e frac 1 2 int 0 T Y s 2 ds right lt infty olmasidir Bu durumda W t Wt 0tYsds displaystyle tilde W t W t int 0 t Y s ds tanimlanirsa her t 0 T displaystyle t in 0 T icin bir P displaystyle tilde mathbb P Brown hareketi elde edilir Finansta kullanimiWt displaystyle W t bir P displaystyle mathbb P olasilik olcusu altinda Brown hareketi m r R displaystyle mu r in mathbb R s gt 0 displaystyle sigma gt 0 ve dSt St mdt sdWt displaystyle dS t S t mu dt sigma dW t olsun Her t gt 0 displaystyle t gt 0 icin 8t m rs displaystyle theta t frac mu r sigma ve zt 0t8sdWs displaystyle zeta t int 0 t theta s dW s tanimlansin O zaman Lt e 0t8sdWs 12 0t8s2ds displaystyle L t e int 0 t theta s dW s frac 1 2 int 0 t theta s 2 ds icin dLt 8LtdWt displaystyle dL t theta L t dW t olur Eger Q Ft LtP Ft displaystyle mathbb Q mathcal F t L t mathbb P mathcal F t olarak tanimlanirsa Bt Wt 8t displaystyle B t W t theta t sureci Q displaystyle mathbb Q olcusu altinda Brown hareketi olur Q displaystyle mathbb Q ya matematiksel finansta riske duyarsiz olcu denir Black Scholes formulunun bir kaniti bu olcu altinda verilebilir Notlar Karatzas amp Shreve 1991 s 302 ye bakiniz Zt X displaystyle Z t X ifadesinin aslinda E 0tXsds t displaystyle mathcal E left int 0 t X s ds right t ifadesi oldugu gozden kacmamalidir Burada E displaystyle mathcal E Doleans Dade usteli notasyonudur Karatzas amp Shreve 1991 s 191 e bakiniz Mesela Oksendal 2003 s 155 ten baslayarak degisik varsayimlar altinda bu teoremin uc degisik versiyonu sunulmustur KaynakcaKaratzas Ioannis 1991 Brownian Motion and Stochastic Calculus 2nd Springer Verlag ISBN 978 0 387 97655 6 2003 Stochastic Differential Equations An Introduction with Applications Springer Berlin ISBN 3 540 04758 1
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans