MatematiÄin bir alt dalÄą olan çok deÄiÅkenli karmaÅÄąk analizde, Hefer teoremi, bir holomorfluk bÃķlgesinde tanÄąmlÄą holomorf fonksiyonlarÄąn iki noktadaki deÄer farkÄąnÄąn bu holomorfluk bÃķlgesinin kartezyen çarpÄąmÄąnda tanÄąmlÄą olan baÅka holomorf fonksiyonlar ile bu iki noktanÄąn koordinatlarÄą çarpÄąmlarÄąnÄąn toplamÄą olarak yazÄąlabileceÄini ifade eden bir sonuçtur.
Teorem, Hans Hefer'in adÄąnÄą taÅÄąmaktadÄąr. Sonucun yayÄąnlandÄąÄÄą makale Hans Hefer adÄąyla Karl Stein ve Heinrich Behnke tarafÄąndan yayÄąnlanmÄąÅtÄąr. AynÄą makalede geçen bir dipnotta Hans Hefer'in doÄu cephesinde ÃķldÞÄÞ, bu çalÄąÅmanÄąn ise Hefer'in 1940'daki tezinden toparlandÄąÄÄą yazÄąlmÄąÅtÄąr.
Teoremin ifadesi
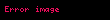
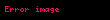

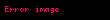
herhangi 
Teoremdeki diÄer fonksiyonlardan Þzerinden yapÄąlan ayrÄąÅÄąm sÃķzde dÄąÅbÞkey olmayan birçok bÃķlgede de mÞmkÞndÞr.
Hefer ÃķnsavÄą
Teoremin kanÄątÄą Hefer ÃķnsavÄą olarak da bilinen bir sonuçtan geçer.
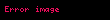
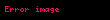

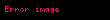
.
O zaman, 
herhangi 
Kaynakça
- ^ Hefer, Hans. "Zur Funktionentheorie mehrerer VerÃĪnderlichen. Ãber eine Zerlegung analytischer Funktionen und die Weilsche Integraldarstellung". Mathematische Annalen. 122 (1950-1951). ss. 276-278. 17 MayÄąs 2022 tarihinde kaynaÄÄąndan arÅivlendi. EriÅim tarihi: 21 EylÞl 2024. (Almanca)
- ^ Boas, Harold (22 Temmuz 2010). "Math 685 Notes Topics in Several Complex Variables" (PDF). 13 EylÞl 2024 tarihinde kaynaÄÄąndan arÅivlendi (PDF). EriÅim tarihi: 21 EylÞl 2024.
- ^ Wiegerinck, Jan (23 AÄustos 2017). "Several Complex Variables" (PDF). 21 EylÞl 2024 tarihinde kaynaÄÄąndan arÅivlendi (PDF). EriÅim tarihi: 21 EylÞl 2024.
wikipedia, wiki, viki, vikipedia, oku, kitap, kÞtÞphane, kÞtÞbhane, ara, ara bul, bul, herÅey, ne arasanÄąz burada,hikayeler, makale, kitaplar, ÃķÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tÞrk, tÞrkçe, turkce, nasÄąl yapÄąlÄąr, ne demek, nasÄąl, yapmak, yapÄąlÄąr, indir, Þcretsiz, Þcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mÞzik, ÅarkÄą, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan cok degiskenli karmasik analizde Hefer teoremi bir holomorfluk bolgesinde tanimli holomorf fonksiyonlarin iki noktadaki deger farkinin bu holomorfluk bolgesinin kartezyen carpiminda tanimli olan baska holomorf fonksiyonlar ile bu iki noktanin koordinatlari carpimlarinin toplami olarak yazilabilecegini ifade eden bir sonuctur Teorem Hans Hefer in adini tasimaktadir Sonucun yayinlandigi makale Hans Hefer adiyla Karl Stein ve Heinrich Behnke tarafindan yayinlanmistir Ayni makalede gecen bir dipnotta Hans Hefer in dogu cephesinde oldugu bu calismanin ise Hefer in 1940 daki tezinden toparlandigi yazilmistir Teoremin ifadesiW Cn displaystyle Omega subset mathbb C n de holomorfluk bolgesi olsun ve f W C displaystyle f Omega mapsto mathbb C holomorf olsun O zaman W W displaystyle Omega times Omega uzerinde tanimli holomorf g1 gn displaystyle g 1 cdots g n fonksiyonlari vardir oyle ki f z f w j 1n zj wj gj w z displaystyle f z f w sum j 1 n z j w j g j w z herhangi z w W displaystyle z w in Omega icin her zaman saglanir Teoremdeki diger fonksiyonlardan uzerinden yapilan ayrisim sozde disbukey olmayan bircok bolgede de mumkundur Hefer onsaviTeoremin kaniti Hefer onsavi olarak da bilinen bir sonuctan gecer W Cn displaystyle Omega subset mathbb C n de holomorfluk bolgesi olsun f W C displaystyle f Omega mapsto mathbb C holomorf fonksiyonu ise W displaystyle Omega nin N k displaystyle N k boyutlu kompleks koordinat uzayiyla kesisiminde tamamen sifir olsun yani f 0 0 zk 1 zk zn 0 displaystyle f 0 cdots 0 z k 1 z k cdots z n equiv 0 O zaman W displaystyle Omega uzerinde tanimli holomorf g1 gn displaystyle g 1 cdots g n fonksiyonlari vardir oyle ki f z j 1nzjgj z displaystyle f z sum j 1 n z j g j z herhangi z W displaystyle z in Omega icin her zaman saglanir Kaynakca Hefer Hans Zur Funktionentheorie mehrerer Veranderlichen Uber eine Zerlegung analytischer Funktionen und die Weilsche Integraldarstellung Mathematische Annalen 122 1950 1951 ss 276 278 17 Mayis 2022 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Eylul 2024 Almanca Boas Harold 22 Temmuz 2010 Math 685 Notes Topics in Several Complex Variables PDF 13 Eylul 2024 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 21 Eylul 2024 Wiegerinck Jan 23 Agustos 2017 Several Complex Variables PDF 21 Eylul 2024 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 21 Eylul 2024
 AzÉrbaycanca
AzÉrbaycanca ÐÐĩÐŧаŅŅŅКŅ
ÐÐĩÐŧаŅŅŅКŅ Dansk
Dansk Deutsch
Deutsch EspaÃąola
EspaÃąola Français
Français Indonesia
Indonesia Italiana
Italiana æĨæŽčŠ
æĨæŽčŠ ŌазаŌ
ŌазаŌ Lietuvos
Lietuvos Nederlands
Nederlands PortuguÊs
PortuguÊs Ð ŅŅŅКÐļÐđ
Ð ŅŅŅКÐļÐđ ā·ā·āķā·āķ―
ā·ā·āķā·āķ― āđāļāļāđāļāļĒ
āđāļāļāđāļāļĒ TÞrkçe
TÞrkçe ÐĢКŅаŅÐ―ŅŅКа
ÐĢКŅаŅÐ―ŅŅКа äļåäšš
äļåäšš United State
United State Afrikaans
Afrikaans