Heisenberg belirsizliği

Belirsizlik ilkesi, Heisenberg belirsizlik ilkesi ya da Belirlenemezlik ilkesi olarak da bilinir.

1927'de Alman fizikçi Werner Heisenberg tarafından ortaya atılan ve bir cismin belirli bir andaki konumu ile momentumunun (Kütlesiyle hızının çarpımının) aynı anda ve kesin değerlerle kuramsal olarak bile ölçülemeyeceğini öne süren ilke. Belirsizlik ilkesi, kuantum mekaniğini klasik fizikten ayıran temel özelliklerin başında gelir ve klasik fiziğin tanımladığı günlük olaylar bu ilkeye ilişkin hiçbir ipucu vermez. Örneğin bir otomobilin belli bir anda bulunduğu yeri ölçmek kolaydır ve bu ölçümlere kesin gözüyle bakılabilir; çünkü bu ilkede söz konusu edilen belirsizlikler, elle tutulup gözle görülebilen her nesne için olduğu gibi otomobil içinde ölçülemeyecek kadar küçüktür. Bu kurala göre, bir cismin ve momentumundaki belirsizliklerin çarpımı, olağan değerlerden çok daha küçük olan bir fiziksel niceliğe ya da sabite ( ${\displaystyle y.10^{-34}}$ joule-saniye; yani h, Planck sabiti olmak üzere, h/2 π niceliğinin değeri) eşit ya da bu nicelikten daha büyük olmalıdır. Bu nedenle, bu belirsizliklerin çarpımı yalnızca kütleleri ve boyutları olağanüstü küçük olan atomlar ve temel parçacıklar için büyük önem taşır.

Elektron gibi bir temel parçacığın hızını, daha doğrusu momentumunun kesin değeriyle ölçmeye kalkışmak, bu parçacığın yerini, önceden kestirilemeyecek biçimde değiştirir; bu nedenle, parçacığın hızını (momentumunu) ölçerken aynı anda yerini de belirlemeye çalışmanın hiçbir anlamı kalmaz. Ölçü aletlerinin, ölçme tekniklerinin ya da gözlemcinin yetersizliğiyle hiçbir ilgisi olmayan bu sonuç, doğada, atomaltı boyutlardaki parçacıklar ve dalgalar arasında var olan yakın bağlantıdan doğar.

Louis de Broglie'nin göstermiş olduğu gibi, her parçacığa bir dalga eşlik eder; başka bir deyişle her parçacık bir dalga davranışı ve özelliği gösterir. Parçacığın, kendisine eşlik eden dalga içinde bulunma olasılığının en yüksek olduğu yerler, dalga genliğinin en büyük olduğu noktalardır. Ne var ki, eşlik eden dalganın genliği ne kadar büyük olursa, ilgili parçacığın momentumuyla hemen hemen özdeş olan ve momentumunu belirleyen dalga boyunu tanımlamak da o kadar güçleşir; çünkü bölge daraldıkça daha çok sayıda dalga boyu bileşeni gerekir. Bu nedenler çok dar bir alana sıkıştırılmış olan bir dalganın eşlik ettiği parçacığın yeri bellidir, ama momentumu için sonsuz sayıda değer bulunabilir. Oysa, tek bir dalga boyuna sahip bir dalga aynı genlikle bütün uzayı kaplayacağından, bu dalganın eşlik ettiği parçacığın hızı (momentumu) hemen hemen kesin olarak belirlenebilir, ama yeri hiçbir zaman bilinemez; daha doğrusu böyle bir parçacık herhangi bir yerde bulunabilir. Yer ile momentumun, yalnız klasik fizikte değil kuantum mekaniğinde de eşlenik olduğu göz önüne alınarak bu ilke genişletilirse, gözlenebilir bir büyüklüğün oldukça önemli bir belirsizliğe yol açar. Bu durum ve genel tanımıyla belirsizlik ilkesi, örneğin enerji ve zaman gibi tüm eşlenik değişken çiftleri için geçerlidir: Enerji ölçümünde söz konusu olan belirsizlik ile ölçümün yapıldığı zaman aralığındaki belirsizliğin çarpımı gene h/2π'ye en azından eşittir. Kararsız bir atom ya da atom çekirdeğinin, daha kararlı bir duruma geçmek için atması gereken enerji miktarının belirsizliği ile kararsız durumda geçirdiği ortalama sürenin belirsizliği arasında da aynı bağıntı söz konusudur.

Matematiksel Detay

Heisenberg bağıntısını ortaya koyduğunda, argümanı yalnızca nitel örneklere dayanıyordu. Bağıntılarının genel ve kesin bir türevini vermemiştir. Aslında, δq belirsizliklerinin bir tanımını bile vermemiştir. vb. bu ilişkilerde ortaya çıkmaktadır.

Elbette bu, o makalenin ilan edilen hedefiyle, yani basit deneyler için kuantum mekaniğinin niteliksel olarak anlaşılmasını sağlamakla tutarlıydı. Belirsizlik ilişkilerinin matematiksel olarak ilk kesin formülasyonu Kennard'a aittir. , 1927 yılında, tüm normalleştirilmiş durum vektörleri için |ψ⟩ aşağıdaki eşitsizlik geçerlidir:

${\displaystyle \Delta _{\psi }P\Delta _{\psi }Q\geq h/2}$

Burada, ΔψP ve ΔψQ durum vektöründeki konum ve momentumun standart sapmalarıdır |ψ⟩

yani,

${\displaystyle (\Delta _{\psi }P)^{2}=\langle P^{2}\rangle _{\psi }-\langle P\rangle _{\psi }^{2}}$

${\displaystyle (\Delta _{\psi }Q)^{2}=\langle Q^{2}\rangle _{\psi }-\langle Q\rangle _{\psi }^{2}}$

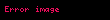
burada ⟨⋅⟩ψ=⟨ψ∣⋅∣ψ⟩ durumundaki beklenti değerini ifade eder |ψ⟩. Eşdeğer olarak ψ(q) dalga fonksiyonunu kullanabiliriz. ve Fourier dönüşümü:

${\displaystyle \psi (q)=\langle q|\psi \rangle }$

${\displaystyle {\overline {\psi }}(p)=\langle p|\psi \rangle =1/\surd 2\pi h\int dqe^{-ipq/h}\psi (q)}$

yazmak için

${\displaystyle (\Delta _{\psi }Q)^{2}=\int dq|\psi (q)|^{2}q^{2}-{\Bigl (}\int dq|\psi (q)|^{2}q){\Bigr )}^{2}}$

${\displaystyle (\Delta _{\psi }P)^{2}=\int dp|\psi (p)|^{2}p^{2}-{\Bigl (}\int dp|\psi (p)|^{2}p){\Bigr )}^{2}}$

Bu eşitsizlik Robertson (1929) tarafından genelleştirilmiş ve tüm gözlemlenebilirler (öz-eşlenik operatörler) için A ve B:

${\displaystyle \Delta _{\psi }A\Delta _{\psi }B\geq 1/2|\langle [A,B]\rangle _{\psi }|}$

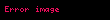
burada [A,B]:= AB-BA komütatörü gösterir.

Heisenberg'in orijinal yarı niceliksel formülasyonunun aksine, yukarıdaki eşitsizlikler kesin olma erdemine sahip olduğundan, bunları Heisenberg'in bağıntılarının tam karşılığı olarak görmek caziptir. Aslında, Heisenberg'in kendi görüşü de böyleydi. Chicago Dersleri'nde Kennard'ın bağıntı türetimini sunmuş ve "bu ispatın matematiksel içerik olarak yarı niceliksel argümanından hiç farklı olmadığını", tek farkın şimdi "ispatın tam olarak gerçekleştirilmesi" olduğunu iddia etmiştir.

Ancak Kennard'ın eşitsizliği ile Heisenberg'in önceki formülasyonu arasında hem statü hem de amaçlanan rol açısından bir fark olduğunu belirtmek faydalı olabilir. Burada tartışılan eşitsizlikler ampirik olgu ifadeleri değil, kuantum mekaniksel formalizmin teoremleridir. Bu nedenle, sezgisel içeriğini açıklamaktan veya bu formalizmin geçerliliği için "alan" veya "özgürlük" yaratmaktan ziyade, bu formalizmin ve özellikle de komütasyon ilişkisinin geçerliliğini varsayarlar. En iyi ihtimalle, yukarıdaki eşitsizlikleri, formalizmin Heisenberg'in ampirik ilkesiyle tutarlı olduğunu göstermek olarak görmek gerekir.

ile arasında kayda değer ikinci bir fark daha vardır. Heisenberg "belirsizlikler" δp için genel bir tanım vermemiştir. Bununla beraber δq. Bunlar hakkında yaptığı en kesin açıklama, bunların "ortalama hata gibi bir şey" olarak alınabileceğiydi. Düşünce deneyleri tartışmalarında, o ve Bohr belirsizlikleri her zaman eldeki deneyle ilgili olan bazı parametreleri seçerek duruma göre ölçerdi. Buna karşılık, eşitsizlikler ve "belirsizlik" ölçüsü olarak tek bir spesifik ifade kullanırlar: standart sapma. O zamanlar, bu ifadenin hata teorisinde ve istatistiksel dalgalanmaların tanımlanmasında iyi bilindiği ve yaygın olarak kullanıldığı göz önüne alındığında, bu seçim doğal değildi. Ancak, bu seçimin belirsizlik ilişkilerinin genel bir formülasyonu için uygun olup olmadığı konusunda çok az tartışma vardı ya da hiç yoktu. Standart sapma, belirli bir durumdaki bir gözlemlenebilirin bir dizi ölçümündeki yayılmayı veya beklenen dalgalanmaları yansıtır. Bu fikri, bir mikroskobun çözümleme gücü gibi bir ölçümün "yanlışlığı" kavramıyla ilişkilendirmek hiç de kolay değildir. Aslında, Heisenberg Kennard'ın eşitsizliğini belirsizlik ilişkisinin kesin formülasyonu olarak almış olsa da, o ve Bohr düşünce deneylerine ilişkin birçok tartışmalarında hiçbir zaman standart sapmalara dayanmamışlardır ve aslında bu tartışmaların standart sapmalar açısından çerçevelenemeyeceği gösterilmiştir (Uffink ve Hilgevoord 1985; Hilgevoord ve Uffink 1988).

Titreşim sayısı ve enerji niceliği az ${\displaystyle \Rightarrow }$ Dalga boyu uzun ${\displaystyle \Rightarrow }$ Bekleme süresi uzun ${\displaystyle \Rightarrow }$ Belirsizlik büyük

Titreşim sayısı ve enerji niceliği çok ${\displaystyle \Rightarrow }$ Dalga boyu kısa ${\displaystyle \Rightarrow }$ Bekleme süresi kısa ${\displaystyle \Rightarrow }$ Belirsizlik küçük

Enerji niceliği ne denli azsa, aynı oranda dalga boyuyla bağlantılı olarak bekleme süresi uzar ve ölçülen zaman belirsizleşir. Tersine; Enerji niceliği ne denli çoksa, aynı oranda dalga boyuyla bağlantılı olarak bekleme süresi azalır ve ölçülen zamanın belirsizliği azalır.

Kaynakça