Helmholtz bobini tekdüze üretmeye yarayan bir alettir. Adını Alman fizikçi Hermann von Helmholtz’dan almıştır. Helmholtz bobini aynı eksendeki iki solenoid elektromıknatısından oluşur. Elektromanyetik alan oluşturmalarının yanı sıra, Helmholtz bobini aynı zamanda dış manyetik alanı nötrleştirmek için de kullanılır. Dünyanın manyetik alanı buna örnektir.


Tanım
Helmholtz bobini solenoid diye adlandırılan iki özdeş dairesel manyetik bobinden oluşur. Helmholtz bobinini oluşturabilmek için solenoidler aynı eksene simetrik olarak yerleştirilip, yarıçap 

Bobinlerin merkezindeki manyetik alan farklılığını en aza indirmek için 

Birkaç uygulamada, Dünya'nın manyetik alanını nötrleştirmek için kullanılan Helmholtz bobini, sıfıra çok yakın bir manyetik alan şiddeti üretir.
Matematik


Uzayda herhangi bir noktadaki kesin manyetik alan hesabı, matematiksel olarak karışık olmakla birlikte Bessel fonksiyonunun uygulama alanına girer. Bobin çifti boyunca olan eksen baz alındığında hesaplama daha kolaylaşır ve alan şiddetinin Taylor serisi genişlemesiyle bulunan ve eksen boyunca bobin çiftlerinin merkez noktalarında uzaklıklarını mesafesi olarak alınması uygundur. Simetrik olarak, genişlemedeki tek mertebe terimleri sıfırdır. Orijin noktası alan şiddeti için büküm noktası olabilsin diye, bir tane bobinin 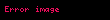


Merkez noktasındaki manyetik alanının kesin değeri aşağıda ayrıntılı olarak verilmiştir. (Yarıçap = R, bobin sayısı = n, bobinlerin akımı =I, manyetik akı yoğunluğu = B)
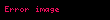

Türev
Tek telli döngünün oluşturduğu eksenüstü alan için oluşturulan formülle başlanır. (Biot-savart yasası
= geçirgenlik sabiti =
= bobibin akımı, amper
= bobinin yarıçapı, metre
= bobin uzaklığı, metre
Helmholtz bobini n tane sarım sayısı içerir.
Orta noktadaki alan şiddeti:
Bir tane bobin yerine iki tane bobin de olabilir. (Birinci bobin, x=0 noktasındaki bobindir; ikinci bobin ise, x=R noktasındaki bobindir.) Simetriden dolayı, orta noktadaki alan şiddeti tek bobinin oluşturduğu değerin iki katı kadar olacaktır.
Maxwell bobini
Bobinlerin uzayda oluşturduğu alanın özdeşliklerini arttırabilmek amacıyla, ek bobinler dışarıdan eklenebilir. 1873 yılında James Clerk Maxwell, iki Helmholtz bobininin arasına daha büyük çaplı bir bobin yerleştirmiştir ve alan sapmalarını azaltan bu bobine bazen Maxwell bobini de denir.
Kaynakça
- https://en.wikipedia.org/wiki/Helmholtz_coil 4 Mart 2015 tarihinde Wayback Machine sitesinde arşivlendi.
- http://www.lightandmatter.com/html_books/0sn/ch11/ch11.html 3 Haziran 2011 tarihinde Wayback Machine sitesinde .
- http://circuitcellar.com/library/print/0606/Wotiz191/5.htm []
- http://hyperphysics.phy-astr.gsu.edu/HBASE/magnetic/curloo.html#c3 17 Ekim 2018 tarihinde Wayback Machine sitesinde .
- http://radphys4.c.u-tokyo.ac.jp/asacusa/wiki/index.php?Cusp%20trap 20 Ocak 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Helmholtz bobini tekduze uretmeye yarayan bir alettir Adini Alman fizikci Hermann von Helmholtz dan almistir Helmholtz bobini ayni eksendeki iki solenoid elektromiknatisindan olusur Elektromanyetik alan olusturmalarinin yani sira Helmholtz bobini ayni zamanda dis manyetik alani notrlestirmek icin de kullanilir Dunyanin manyetik alani buna ornektir Helmholtz bobiniHelmholtz bobininin sistematik cizimiTanimHelmholtz bobini solenoid diye adlandirilan iki ozdes dairesel manyetik bobinden olusur Helmholtz bobinini olusturabilmek icin solenoidler ayni eksene simetrik olarak yerlestirilip yaricap R displaystyle R ye esit olacak sekilde h displaystyle h uzakliginda birbirinden ayrilir Her iki bobin de ayni dogrultuda esit miktarda elektrik akimi elde eder Bobinlerin merkezindeki manyetik alan farkliligini en aza indirmek icin h R displaystyle h R olarak kabul edilir ama bobinlerin merkezleri ve duzlemler arasindaki alan siddetlerinde 7 oraninda degisim vardir Biraz daha buyuk olan h displaystyle h degeri duzlem ve merkezler arasinda kalan alanlardaki farklilik oranini dusurur Birkac uygulamada Dunya nin manyetik alanini notrlestirmek icin kullanilan Helmholtz bobini sifira cok yakin bir manyetik alan siddeti uretir MatematikAkim dongusunu iki esit parcaya bolen duzlemdeki manyetik alan cizgileriBobin ciftinin yanindaki manyetik alan miktarini gosteren kontur Uzayda herhangi bir noktadaki kesin manyetik alan hesabi matematiksel olarak karisik olmakla birlikte Bessel fonksiyonunun uygulama alanina girer Bobin cifti boyunca olan eksen baz alindiginda hesaplama daha kolaylasir ve alan siddetinin Taylor serisi genislemesiyle bulunan ve eksen boyunca bobin ciftlerinin merkez noktalarinda uzakliklarini mesafesi olarak alinmasi uygundur Simetrik olarak genislemedeki tek mertebe terimleri sifirdir Orijin noktasi alan siddeti icin bukum noktasi olabilsin diye bir tane bobinin x2 displaystyle x 2 terimi ayni zamanda 0 olmalidir ve bunun icin onculuk eden ve sabit olmayan x4 displaystyle x 4 terimi kullanilir Basit bobin icin bukum noktasi kendi merkezine kadar mesafede bobin ekseni dogrultusunda konumu belirlenir Boylece iki bobinin konumu x R 2 displaystyle x pm R 2 seklinde belirlenir Merkez noktasindaki manyetik alaninin kesin degeri asagida ayrintili olarak verilmistir Yaricap R bobin sayisi n bobinlerin akimi I manyetik aki yogunlugu B B 45 3 2m0nIR displaystyle B left frac 4 5 right 3 2 frac mu 0 nI R m0 displaystyle mu 0 boslugun gecirgenligidir 4p 10 7 T m A displaystyle 4 pi times 10 7 text T cdot text m A Turev Tek telli dongunun olusturdugu eksenustu alan icin olusturulan formulle baslanir Biot savart yasasi B1 x m0IR22 R2 x2 3 2 displaystyle B 1 x frac mu 0 IR 2 2 R 2 x 2 3 2 m0 displaystyle mu 0 gecirgenlik sabiti 4p 10 7 T m A 1 257 10 6 T m A displaystyle 4 pi times 10 7 text T cdot text m A 1 257 times 10 6 text T cdot text m A I displaystyle I bobibin akimi amper R displaystyle R bobinin yaricapi metre x displaystyle x bobin uzakligi metre Helmholtz bobini n tane sarim sayisi icerir B1 x m0nIR22 R2 x2 3 2 displaystyle B 1 x frac mu 0 nIR 2 2 R 2 x 2 3 2 Orta noktadaki alan siddeti B1 R2 m0nIR22 R2 R 2 2 3 2 displaystyle B 1 left frac R 2 right frac mu 0 nIR 2 2 R 2 R 2 2 3 2 Bir tane bobin yerine iki tane bobin de olabilir Birinci bobin x 0 noktasindaki bobindir ikinci bobin ise x R noktasindaki bobindir Simetriden dolayi orta noktadaki alan siddeti tek bobinin olusturdugu degerin iki kati kadar olacaktir B R2 2B1 R 2 2m0nIR22 R2 R 2 2 3 2 m0nIR2 R2 R 2 2 3 2 m0nIR2 R2 14R2 3 2 m0nIR2 54R2 3 2 45 3 2m0nIR 855 m0nIR displaystyle begin aligned B left frac R 2 right amp 2B 1 R 2 amp frac 2 mu 0 nIR 2 2 R 2 R 2 2 3 2 frac mu 0 nIR 2 R 2 R 2 2 3 2 amp frac mu 0 nIR 2 R 2 frac 1 4 R 2 3 2 frac mu 0 nIR 2 frac 5 4 R 2 3 2 amp left frac 4 5 right 3 2 frac mu 0 nI R amp left frac 8 5 sqrt 5 right frac mu 0 nI R end aligned Maxwell bobiniBobinlerin uzayda olusturdugu alanin ozdesliklerini arttirabilmek amaciyla ek bobinler disaridan eklenebilir 1873 yilinda James Clerk Maxwell iki Helmholtz bobininin arasina daha buyuk capli bir bobin yerlestirmistir ve alan sapmalarini azaltan bu bobine bazen Maxwell bobini de denir Kaynakcahttps en wikipedia org wiki Helmholtz coil 4 Mart 2015 tarihinde Wayback Machine sitesinde arsivlendi http www lightandmatter com html books 0sn ch11 ch11 html 3 Haziran 2011 tarihinde Wayback Machine sitesinde http circuitcellar com library print 0606 Wotiz191 5 htm olu kirik baglanti http hyperphysics phy astr gsu edu HBASE magnetic curloo html c3 17 Ekim 2018 tarihinde Wayback Machine sitesinde http radphys4 c u tokyo ac jp asacusa wiki index php Cusp 20trap 20 Ocak 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans









