Matematiğin bir alt dalı olan karmaşık analizde, holomorfluk bölgesi, üzerinde tanımlı olan holomorf fonksiyolardan en az bir tanesinin daha büyük bir bölgeye holomorf özelliğini koruyarak devam ettirelemediği bölgelere verilen addır. Karmaşık düzlemdeki açık kümelerin hepsi holomorfluk bölgesidir. Ancak, karmaşık düzlemde geçerli olan bu sonucun dengi bir sonuç yüksek boyutlu uzayda herhangi bir bölge için geçerli değildir. Bu yüzden, holomorfluk bölgelerin belirleyici özelliklerini bulmak yirminci yüzyılın ilk yarısında çok değişkenli karmaşık analizde en yoğun çalışılmış konulardan birisi olmuştur. Bu farklılığı ilk defa Fritz Hartogs göz önüne sermiştir ve sonuç en genel haliyle Hartogs devam (genişleme) teoremi olarak bilinmektedir.
Tanım

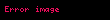



.
bağlantılı ve
.
üzerinde tanımlı her holomorf
fonksiyonu için, tanım kümesi
olan ve
üzerinde
sağlayan holomorf bir
vardır.
Denk tanımlar
Holomorfluk bölgesinin tanımına denk olan başka matematiksel ifadeler de vardır. Bu amaçla, 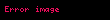
holomorfluk bölgesidir.
. Yani,
'nın tıkız altkümelerinin
içindeki
içinde yine tıkızdır.
üzerinde tanımlı holomorf fonksiyonların kümesi
ile gösterilirse, tıkız bir
için holomorf dışbükey kaplam şu şekilde tanımlanır:
sözde dışbükey bölgedir.
üzerinde vardır. Yani,
kümeleri
içinde yer alan kapalı ve
ise, o zaman
olur.
yerel Levi özelliğine sahiptir:
'nın sınırındaki her nokta için bir komşuluk vardır öyle ki bu komşuluğun
ile kesişiminde holomorf olan hiçbir fonksiyon komşuluğun tümüne holomorf olarak devam ettirilemez.


Özellikler
holomorfluk bölgesi ise, o zaman kesişimleri
de holomorfluk bölgesi olur.
bir öncekini kapsayarak artan bir holomorfluk bölge dizisi ise, o zaman bu bölgelerin birleşimleri
de holomorfluk bölgesidir. Bu özellik Behnke-Stein teoremi olarak da bilinir.
ve
holomorfluk bölgesi ise, o zaman
de holomorfluk bölgesidir.
- Birinci bir holomorfluk bölgesinde her zaman çözülebilir. İkinci ise ilave topolojik varsayımlar eklenerek çözülebilir.
Karmaşık düzlemde sonuçlar
Karmaşık düzlemdeki açık kümelerin hepsi holomorfluk bölgesidir. Karmaşık düzleme eşit olmayan açık kümenin holomorfluk bölgesi olduğunu göstermek için genelde iki ayrı yöntem takip edilir. Ya fonksiyonun sıfır değeri aldığı noktaların kümeye eşit olmadığı ve kümenin sınırındaki her noktaya yığılması istenir ya da fonksiyonun sınırdaki noktalara doğru limitinin sonsuz olması istenir. Mesela, açık kümenin sınırının her noktasına yığılma gösteren ama herhangi bir şekilde içerideki bir noktaya yığılmayan karmaşık sayı dizisi inşa edilebilir. O zaman, Weierstrass çarpım teoreminin bir genellemesi yardımıyla, bu bölge üzerinde holomorf olan ve bu dizinin yığılma noktalarında sıfır değerleri olan bir fonksiyon vardır. Bu fonksiyonun çarpmaya göre tersi, açık kümenin üzerinde tanımlı ve holomorftur. Bu sayede, bu kümenin dışına holomorf olarak devam ettirilemez.
Örnekler
- sayesinde, kuvvetleri belli tamsayıları atlayan (boşluklu) seriler birim diskin dışına holomorf bir şekilde genişletilemez. Mesela,
tamsayı olmak üzere
serisi birim diskin dışına holomorf olarak devam ettirilemez.
- Başka bir örnek ise
serisidir.
- Aynı türden başka bir örnek ise
serisidir.
de birim diskin dışına holomorf bır şekilde devam ettirilemeyen holomorf bir fonksiyondur.
Ayrıca bakınız
Notlar
- ^ (Greene & Krantz 2006, s. 268)
Kaynaklar
- Greene, R. E; Krantz, S. G. (2006). Function theory of one complex variable. Providence, RI: American Mathematical Society.
- Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.
- Boris Vladimirovich Shabat, Introduction to Complex Analysis, AMS, 1992
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan karmasik analizde holomorfluk bolgesi uzerinde tanimli olan holomorf fonksiyolardan en az bir tanesinin daha buyuk bir bolgeye holomorf ozelligini koruyarak devam ettirelemedigi bolgelere verilen addir Karmasik duzlemdeki acik kumelerin hepsi holomorfluk bolgesidir Ancak karmasik duzlemde gecerli olan bu sonucun dengi bir sonuc yuksek boyutlu uzayda herhangi bir bolge icin gecerli degildir Bu yuzden holomorfluk bolgelerin belirleyici ozelliklerini bulmak yirminci yuzyilin ilk yarisinda cok degiskenli karmasik analizde en yogun calisilmis konulardan birisi olmustur Bu farkliligi ilk defa Fritz Hartogs goz onune sermistir ve sonuc en genel haliyle Hartogs devam genisleme teoremi olarak bilinmektedir TanimTanimdaki kumeler W Cn displaystyle Omega subset mathbb C n acik bir kume olsun Asagidaki kosullari saglayan W1 displaystyle Omega 1 ve W2 displaystyle Omega 2 gibi acik kumeler yoksa W displaystyle Omega ya holomorfluk bolgesi denir W1 W2 W displaystyle emptyset neq Omega 1 subset Omega 2 cap Omega W2 displaystyle Omega 2 baglantili ve W2 W displaystyle Omega 2 not subset Omega W displaystyle Omega uzerinde tanimli her holomorf f displaystyle f fonksiyonu icin tanim kumesi W2 displaystyle Omega 2 olan ve W1 displaystyle Omega 1 uzerinde f g displaystyle f g saglayan holomorf bir g displaystyle g vardir Denk tanimlarHolomorfluk bolgesinin tanimina denk olan baska matematiksel ifadeler de vardir Bu amacla W Cn displaystyle Omega subset mathbb C n bir bolge olsun O zaman asagidaki ifadeler birbirine denktir W displaystyle Omega holomorfluk bolgesidir W displaystyle Omega Yani W displaystyle Omega nin tikiz altkumelerinin W displaystyle Omega icindeki W displaystyle Omega icinde yine tikizdir W displaystyle Omega uzerinde tanimli holomorf fonksiyonlarin kumesi O W displaystyle mathcal O Omega ile gosterilirse tikiz bir K W displaystyle K subset Omega icin holomorf disbukey kaplam su sekilde tanimlanir K W z W f z supw K f w f O W displaystyle displaystyle hat K Omega left z in Omega f z leq sup w in K f w quad forall f in mathcal O Omega right W displaystyle Omega sozde disbukey bolgedir W displaystyle Omega uzerinde vardir Yani a displaystyle triangle alpha kumeleri W displaystyle Omega icinde yer alan kapali ve a a W displaystyle cup alpha partial triangle alpha subset Omega ise o zaman a a W displaystyle cup alpha triangle alpha subset Omega olur W displaystyle Omega yerel Levi ozelligine sahiptir W displaystyle Omega nin sinirindaki her nokta icin bir komsuluk vardir oyle ki bu komsulugun W displaystyle Omega ile kesisiminde holomorf olan hicbir fonksiyon komsulugun tumune holomorf olarak devam ettirilemez 1 3 displaystyle 1 Rightarrow 3 Oka onsavi yardimiyla cozulur 5 1 displaystyle 5 Rightarrow 1 ise olarak bilinir Ilk defa Kiyoshi Oka tarafindan cozulmustur OzelliklerW1 Wn displaystyle Omega 1 dots Omega n holomorfluk bolgesi ise o zaman kesisimleri W j 1nWj displaystyle Omega bigcap j 1 n Omega j de holomorfluk bolgesi olur W1 W2 displaystyle Omega 1 subseteq Omega 2 subseteq dots bir oncekini kapsayarak artan bir holomorfluk bolge dizisi ise o zaman bu bolgelerin birlesimleri W n 1 Wn displaystyle Omega bigcup n 1 infty Omega n de holomorfluk bolgesidir Bu ozellik Behnke Stein teoremi olarak da bilinir W1 displaystyle Omega 1 ve W2 displaystyle Omega 2 holomorfluk bolgesi ise o zaman W1 W2 displaystyle Omega 1 times Omega 2 de holomorfluk bolgesidir Birinci bir holomorfluk bolgesinde her zaman cozulebilir Ikinci ise ilave topolojik varsayimlar eklenerek cozulebilir Karmasik duzlemde sonuclarKarmasik duzlemdeki acik kumelerin hepsi holomorfluk bolgesidir Karmasik duzleme esit olmayan acik kumenin holomorfluk bolgesi oldugunu gostermek icin genelde iki ayri yontem takip edilir Ya fonksiyonun sifir degeri aldigi noktalarin kumeye esit olmadigi ve kumenin sinirindaki her noktaya yigilmasi istenir ya da fonksiyonun sinirdaki noktalara dogru limitinin sonsuz olmasi istenir Mesela acik kumenin sinirinin her noktasina yigilma gosteren ama herhangi bir sekilde icerideki bir noktaya yigilmayan karmasik sayi dizisi insa edilebilir O zaman Weierstrass carpim teoreminin bir genellemesi yardimiyla bu bolge uzerinde holomorf olan ve bu dizinin yigilma noktalarinda sifir degerleri olan bir fonksiyon vardir Bu fonksiyonun carpmaya gore tersi acik kumenin uzerinde tanimli ve holomorftur Bu sayede bu kumenin disina holomorf olarak devam ettirilemez Ornekler sayesinde kuvvetleri belli tamsayilari atlayan bosluklu seriler birim diskin disina holomorf bir sekilde genisletilemez Mesela a 2 displaystyle a geq 2 tamsayi olmak uzere n 0 zan displaystyle sum n 0 infty z a n serisi birim diskin disina holomorf olarak devam ettirilemez Baska bir ornek ise n 0 zn displaystyle sum n 0 infty z n serisidir Ayni turden baska bir ornek ise n 0 z2n displaystyle sum n 0 infty z 2 n serisidir n 0 1 z2n displaystyle prod nu 0 infty 1 z 2 nu de birim diskin disina holomorf bir sekilde devam ettirilemeyen holomorf bir fonksiyondur Ayrica bakinizBehnke Stein teoremi Sozde disbukeylikNotlar Greene amp Krantz 2006 s 268 KaynaklarGreene R E Krantz S G 2006 Function theory of one complex variable Providence RI American Mathematical Society Steven G Krantz Function Theory of Several Complex Variables AMS Chelsea Publishing Providence Rhode Island 1992 Boris Vladimirovich Shabat Introduction to Complex Analysis AMS 1992
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans




















