Hubble kanunu, fiziksel kozmolojide gözlemlere verilen isimdir: uzayın derinliklerinde gözlenen nesnelerin dünyadan uzak göreceli bir hızda yorumlanabilir bir Doppler kaymasına sahip olduğu bulunur ve dünyanın gerisinde kalan çeşitli galaksilerin bu Doppler kaymasıyla ölçülen hızı yaklaşık birkaç yüz ışık yılı uzaklığındaki galaksiler için uzaklıklarıyla doğru orantılıdır. Bu normal olarak gözlemlenebilir evrenin uzaysal hacminin genişlemesinin doğrudan bir gözlemi olarak yorumlanır.
Yalnızca bu genişlemeden ötürü olan astronomik nesnelerin devinimi, Hubble akışı olarak bilinir. Hubble kanunu genişleyen uzay paradigması için gözlemlenebilen ilk temel olarak kabul edilir ve günümüzde Big Bang modelinin desteklenmesi için en çok atıfta bulunulan kanıtların parçalarından biri olarak hizmet etmektedir. Hubble kanunu’nun genişleyen uzay paradigması için gözlemlenebilir ilk temel olduğu bilinir ve bugün bu kanun Big Bang teorisi desteğine atfedilen birkaç parça kanıttan birine hizmet eder.
Yaygın olarak Edwin Hubble'a atfedilmesine rağmen, kanun ilk 1927'de Georges Lemaître tarafından yayınlanan bir makalede genel izafiyet denklemlerinden türemiştir. Georges Lemaitre evrenin genişlediğini öne sürmüş ve bu genişleme oranı için tahmini bir değer vermiştir, bu değer şu an Hubble sabiti olarak adlandırılır. Edwin Hubble bu kanunun varlığını onayladıktan iki yıl sonra şu an adıyla anılan sabit için daha doğru bir değer belirlemiştir. Hubble nesnelerin durgun hızları hakkında onların kırmızıya kaymalarından elde ettiği değerlerden bir çıkarım yapmıştır, bu değerlerin birçoğu daha önceleri ölçülmüş ve 1917 yılında Vesto Slipher tarafından bulunan hızla ilişkilendirilmiştir.
Kanun genellikle şu denklemle gösterilir v = H0D, H0 orantılılık sabiti (Hubble sabiti) ile D(zamanı değiştirebilir, birlikte hareket ettiği aralığa benzemez) bir galaksiye “uygun aralık” arası ve hızı v’dir. (kozmolojik zaman koordinatına bağlı olarak uygun aralığın türevidir; ‘hız’ın tanımı hakkındaki daha kurnaz tartışmalar için Uygun aralığın kullanımları’na bakınız.) H0’ın SI birimi s−1 'dir, fakat daha sıklıkla (km/s)/Mpc’den alıntıdır, bir galaksinin km/s için hızına 1 ışık yılı (3.09×1019 km) hızı verir. H0’ın karşılığı Hubble zamanıdır.
Gözlemlenen değerler
| Yayımlanan tarih | Hubble sabiti | Gözlemci | Uyarılar |
|---|---|---|---|
| 2016-11-22 | 71.9+2.4 −3.0 | Hubble Uzay Teleskobu | Kütleçekimsel Merceklenme etkisi ile oluşan birkaç adet değişken ışık kaynağının fotoğrafları arasındaki zaman gecikmesi ile hesaplanmıştır. En güncel Hubble sabitidir. |
| 2016-07-13 | 67.6+0.7 −0.6 | Apache Noktası Gözlemevi'nin Sloan Digital Sky Survey Spektroskobu | |
| 2016-05-17 | 73.00±1.75 | Hubble Uzay Teleskobu | Hubble Uzay Teleskobu'nun Geniş Alan Kamerası () kullanılarak tekrar ölçülmüştür. |
| 2015-02 | 67.74±0.46 | Planck Görevi | Planck Görevi'nin bütün analizlerini içeren bilgiler 1 Aralık 2014'te Ferrara'da yapılan konferansta halka açık bir şekilde paylaşıldı. Görevin detaylı sonuçlarını içeren dokümanların tamamı ise Şubat 2015'te yayınlandı. |
| 2013-03-21 | 67.80±0.77 | Planck Görevi | Mayıs 2009’da başlatıldı. Dört yıllık bir zamandan sonra, WMAP’den daha küçük bir aralıkta CMB ölçümü için HEMT radyometreleri ve bolometri teknolojisini kullanan erken dönem incelemeleri yerine daha önemli ayrıntılı incelemeler yapan kozmik mikrodalga radyasyonunu çalıştırmıştır. Planck kozmoloji aracının arkasındaki Avrupalılar’ın başını çektiği araştırma takımı görevin CMB tüm gökyüzü haritası ve onların belirlediği Hubble sabitinin de aralarında bulunduğu tüm verilerini yayınlamıştır. |
| 2012-12-20 | 69.32±0.80 | WMAP(9 yıllık) | Bu değerler WMAP ve diğer kozmolojik verilerin birleşimi ΛCDM modelinin en basit sürümüne yerleştirilmesiyle ortaya çıkmıştır. Eğer veri daha genel sürümlerle uyumluysa, H0 değeri daha küçük ve daha belirsiz olmaya yatkındır: genellikle 67±4 (km/s)/Mpc civarındaysa da bazı modeller 63 (km/s)/Mpc civarında değer verir. |
| 2010 | 71.0±2.5 | WMAP(7 yıllık) | |
| 2010 | 70.1±1.3 | WMAP (7 yıllık) | |
| 2009-02 | 70.1±1.3 | WMAP(5 yıllık) | |
| 2009-02 | 71.9+2.6 −2.7 | WMAP(5 yıllık) | |
| 2006-08 | 77.6+14.9 −12.5 | Chandra X-ray Gözlemevi | |
| 2007 | 70.4+1.5 −1.6 | WMAP (3 yıllık) | |
| 2001-05 | 72±8 | Hubble Uzay Teleskobu | Bu proje en hassas optik belirlemeyi sağlamış, benzer doğruluğa sahip birçok galaksi kümesinin Sunyaev-Zel’dovich etkisi gözlemlerine dayanandığından uyumludur. |
| 1996 öncesi | 50–90 (tahmini) | ||
| 1958 | 75 (tahmini) | Allan Sandage | H0 için ilki iyi tahmindi,, ama konsensusa varmadan önce on yıllık zaman geçebilirdi. |
Keşfi
Hubble gözlemlerini yapmadan yaklaşık on yıl önce, birçok fizikçi ve matematikçi Einstein’ın genel izafiyet alan denklemlerini kullanarak uzay ve zaman arasında ilişkili bir teori geliştirdiler. Evrenin doğasının en genel ilkelerini uygulayarak dinamik bir çözüm üretildi, fakat yaygın statik evren kavramıyla çatışmaktaydı.
FLRW denklemleri
922’de Alexander Friedmann evrenin ölçülebilir oranda genişleyebileceğini gösteren Einstein’ın alan denklemlerinden kendi Friedmann denklemlerini türetti. Friedmann tarafından kullanılan parametre bugün Hubble kanununun orantılılık sabitinin bir aralık değişkeni gibi düşünüldüğü bir aralık faktörü olarak bilinir. Georges Lemaître benzer bir çözümü 1927’de bağımsız bir şekilde bulmuştu. Friedmann denklemleri, yoğunluk ve basıncı verilen bir akışkan için Einstein'ın alan denklemlerine homojen ve izotropik evren metriği yerleşmesinden türetilir. zaman fikri sonunda kozmolojinin Big Bang ve Kararlı Hal teorilerine kılavuz oldu.
Lemaître denklemi
1927’de Hubble makalesini yayınlamadan iki yıl önce, Belçikalı rahip ve astronom Georges Lemaître, Hubble Kanunu olarak bilinen araştırma türevlerini yayınlayan ilk kişiydi. Maalesef bilinmeyen nedenlerden ötürü, radyal hızlar ve uzaklıklara (ve ilk basit H belirlenmesi) dair tüm araştırması ortadan kalktı” Bu ihmallerin kasıtlı olduğu düşünülür. Kanadalı astronom Sidney van den Bergh’e göre, “Evrenin genişlemesine dair Lemaître’nin 1927 yılında yaptığı keşif düşük etkili bir Fransız dergisinde yayınlandı. 1931’de bu makalenin yüksek etkili İngiliz tercümesinde, kritik bir denklem şu an Hubble sabiti olarak bilinen ortadan kaldırılan bir kaynak ile değiştirildi. Evrenin genişlemesiyle ilgili bu makalenin o kısmı bilinmeyen bir tercümanın ortadan kaldırmasının önerildiği İngiliz tercümesinden de silinmişti.”
Evrenin şekli
keşfinden önce, evrenin boyutu ve şekline dair konuşmalar kayda değerdi. 1920’de ünlü , Harlow Shapley ve Heber D. Curtis arasında geçti. Shapley küçük bir evrende boyutunu tartışırken, Curtis evrenin daha büyük olduğunu savundu. Bu konu gelecek on yıl içinde Hubble’ın geliştirdiği gözlemlerle çözülecekti.
Samanyolu içinde parlaklığı zamanla değişen yıldızlar
Edward Hubble profesyonel astronomik gözlemci araştırmalarının çoğunu zamanında dünyanın en güçlü teleskoplarıba sabit Mount Wilson Gözlemevi'nde yaptı. parlaklığı zamanla değişen yıldızlar hakkındaki gözlemleri, bu nesnelerin mesafesini hesaplamasında olanak sağladı. Sürpriz bir şekilde, bu nesneler Samanyolu dışında oldukları uzaklıklarda keşfedildiler.Bu nesnelere nebulalar denilmeye devam edildi ve yavaş yavaş galaksiler bu terimin yerini aldı.
Uzaklık ölçümleriyle kırmızıya kayan değerleri birleştirme

Hubble kanununundaki parametreler: hızlar ve aralıklar doğrudan ölçülemez. Gerçekte bir mesafe ve kırmızıya kayma z = ∆λ/λ radyasyonun spektrumu hakkında bilgi verir. Hubble parlaklık ve parametre z’yi düzeltir. Galaksi mesafe ölçümlerinin Vesto Slipher ve Milton Humason kırmızıya kayma ölçümleriyle birleşimi galaksilerle ilişkilidir, Hubble bir nesne ve onun uzaklığının kırmızıya kayması arasında zor bir orantı keşfetti. Dikkate değer bir dağılma (özgün hızların neden olduğu bilinir – Hubble akışı durgun hızın özgün hızlardan daha küçük olduğu uzay alanından çok uzak durumları kasteder) olmasına rağmen, Hubble çalıştığı ve 500 km/s/Mpc Hubble sabitini (uzaklık kalibrasyonlarındaki hatalardan dolayı şu an kabul edilen değerden daha yüksek) elde ettiği bir değer olan 46 galaksiden bir eğilim çizgisi çizebildi. (ayrıntılar için kozmik aralık basamağına bakınız)
Hubble kanununun keşfedildiği ve geliştirildiği zaman, özel görecelilik anlamında Doppler kayması gibi kırmızıya kayma olayını açıklamak kabul edilebilir; hızla birlikte kırmızıya kaymayı ilişkilendirmek için Doppler formülünü kullanın. Bugün, Hubble kanununun hız-mesafe ilişkisi, Doppler etkisi değil evrenin genişlemesine kozmolojik bir model sunan kırmızıya kayma ile bağlantılı ve hızla birlikte teorik bir sonuç olarak görülmektedir. Hubble kanununa giren küçük z hızı için, küçük z hızında kırmızıya kayma ilişkisi iki çıkarım için de aynı olmasına rağmen, Doppler etkisi daha fazla yorumlanamaz.
Hubble diyagramı
Hubble kanunu nesnenin hızının gözlemciden uzaklığına (ortalama kırmızıya kayma değerleri ile orantılı olduğu farzedilir) göre çizildiği bir Hubble diyagramında kolayca tarif edilebilir. Bu diyagramda doğrusal çizginin pozitif eğimi Hubble kanununun görsel tasviridir.
Kullanılmayan kozmoloji sabiti
Hubble’ın keşfi yayınlandıktan sonra, Albert Einstein üzerine çalışmayı bıraktı; düzenlemeyi düşündü. Einstein genişleyen veya daralan bir evren için, en basit biçimde, statik bir çözüm yaratabildi. Evrenin aslında genişlediğini gösteren Hubble’ın keşfinden sonra, Einstein yanlış farz ettiği evrenin statik olduğu fikrini “en büyük hatası” olarak kabul etti. Tek başına ele alındığında, deneylerle gözlemlenebilir ve orijinal olarak formülleştirdiği denklemlerin özel çözümlerini kullanarak teorik hesaplamalarını karşılaştırabildiği (büyük kütlelerin ışığı bükmesi veya Merkür gezegeninin devinimi gibi gözlemler boyunca) genel izafiyet evrenin genişlemesini öngörebilirdi.
1931’de Einstein modern kozmolojide gözlemlenebilir bir temel sağlayan Hubble’a teşekkür etmek için Mount Wilson’a gitti.
Kozmoloji sabiti geçmiş on yılda karanlık enerji için bir hipotez olarak tekrar ilgi çekmeye başladı.
Yorum

Kırmızıya kayma ve mesafe arasındaki doğrusal ilişkinin keşfi, durgun hız ve aşağıdaki gibi Hubble kanunu için basit bir matematiksel gösterim oluşturan kırmızıya kayma arasındaki doğrusal hız ile birleşir:

burada,
durgun hızdır, km/s olarak gösterilir.
- H0 Hubble sabitidir ve altsimge 0’ı simgeleyen alınan gözlem zamanında Friedmann denklemleriyle uyumlu
ile gösterilir. (sıklıkla zamana bağlı bir değer olan Hubble parametresidir ve aralık faktörü olarak ifade edilir.
gözlemciden galaksiye uygun aralıktır (zamanla değişebilir, sabit olan birlikte hareket mesafesine benzemez)Durgun zaman: v = dD/dt).
Hubble kanununun durgun hız ve mesafe arasında temel bir ilişki oluşturduğu düşünülür. Ancak, durgun hız ve kırmızıya kayan değerler arasındaki ilişki kabul edilmiş kozmolojik modele bağlıdır ve küçük kırmızı kaymalar dışında oluşmaz. Hubble küresinin yarıçapından rHS daha büyük mesafeler D için, nesneler ışık hızından daha hızlı bir oranda uzaklaşırlar (Önemli bir tartışma için Uygun Aralık Kullanımları’na bakınız.):v = dD/dt).
Hubble “sabiti” zamanda değil, sadece uzayda bir sabit olduğundan, Hubble küresinin yarıçapı çeşitli zaman aralıklarında artabilir ya da azalabilir.
Altsimge '0' bugünkü Hubble sabitini gösterir.
Bugünkü kanıt evrenin hızlanan genişlemesini (Hızlanan evrene bakınız.) öne sürmektedir, yani herhangi bir galaksi için, durgun hız dD/dt galaksiler daha uzağa gittikçe zamanla artmaktadır. Ancak Hubble parametresinin aslında zamanla azaldığı düşünülür. Bu da eğer bazı sabit uzaklıktaki farklı galaksilere bakarsak ve onları izlersek, galaksilerin aynı uzaklıktaki diğer galaksilerden daha küçük bir hızla geçtiği anlamına gelirdi.
Kırmızıya kayma hızı ve durgun hız
Kırmızıya kayma, uzak yıldızsı gökcisimleri için hidrojen α-çizgileri gibi bilinen bir dalgaboyunu belirleyerek ve hareketli bir kaynakla karşılaştırılan önemsiz bir kaymayı bularak ölçülebilir. Bu kırmızıya kayma deneysel gözlemler için kesin bir miktardır. Kırmızıya kayma ve durgun hız ilişkisi diğer bir maddedir. Daha ayrıntılı tartışma için Harrison’a bakınız.
Kırmızıya kayma hızı
Kırmızıya kayma z, genellikle kırmızıya kayma hızı olarak tanımlanır, doğrusal bir Doppler etkisinden dolayı olsaydı durgun hız aynı kırmızı kaymayı oluşturabilirdi (Evrenin kozmolojik genişlemesinin neden olduğu kırmızıya kayma aynı durum değildir, çünkü hızlar Doppler kaymasında göresiz bir formül kullanmak için çok büyüktür.) Bu kırmızıya kayma hızı kolayca ışık hızını aşabilir.Diğer bir deyişle, kırmızıya kayma hızını rHS belirlemedeki ilişkide şu :
kullanılır.
Yani kırmızıya kayma hızı ve kırmızıya kayma arasında önemli bir fark yoktur: katı bir şekilde birbiriyle orantılıdır ve teorik nedenlere dayanmaz. Kırmızıya kayma hızı terminolojisi ötesindeki istek Fizeau-Doppler formülünün düşük bir hızla basitleştirilmesinden oluşan kırmızıya kayma hızıyla uyumludur.
λo, λe sırasıyla gözlemlenen ve gönderilen dalgaboylarıdır. “Kırmızıya kayma hızı” büyük hızlarda gerçek hızla ilgili değildir, ancak bu terminoloji gerçek hız olarak yorumlanırsa bir karmaşa yaratır. Bir sonraki başlıkta kırmızıya kayma veya kırmızıya kayma hızı ve durgun hız arasındaki bağlantı tartışılacaktır. Bu tartışma Sartori’ye dayanır.
Durgun hız
R(t)’nin evrenin aralık faktörü olduğunu farzedin ve o seçilen kozmolojik modele bağlı olacak bir şekilde evrenin genişlemesini arttırır. Birlikte hareket eden noktalar arasında ölçülen mesafelerin R’yi orantılı bir şekilde arttıracağı anlamına gelir.(Birlikte hareket eden noktalar uzayın genişlemesinin bir sonucu olmasının dışında birbirlerine göre göreceli olarak hareket etmez.) Diğer bir deyişle:
Eğer ışık te zamanında bir galaksiden yansırsa ve biz onu t0 zamanında alırsak, evrenin genişlemesinden doğan bir kırmızı kayma oluşur ve bu kırmızı kayma z basitçe şöyledir:
D mesafesinde bir galaksi farz edin ve bu mesafe belli oranda zamanla dtD değişir. Bu durma oranına “durgun hız” vr deriz.
Hubble sabitini şöyle tanımlarız:
Hubble kanunu şöyle keşfederiz:
Bu açıdan Hubble kanunu (i) evrenin genişlemesine katkıda bulunan durgun hız ve (ii) nesnenin uzaklığı arasındaki temel bağlantıdır; kırmızıya kayma ve mesafe arasındaki bağlantı Hubble kanunu ile gözlemleri birbirine bağlamak için kullanılan bir destektir. Bu kanun Taylor serisi genişlemesi yapılarak ortalama bir şekilde kırmızıya kayma z ile ilişkilendirilebilir:
Eğer mesafe çok büyük değilse, modelin diğer tüm zorlukları küçük düzeltmeler olmaya başlar ve zaman aralığı basitçe aralığın ışık hızına bölünmesidir:
or
Bu yaklaşıma göre, cz = vr ilişkisi modele bağlı büyük kırmızıya kaymalarla yer değiştirmesi için düşük kırmızıya kaymalarda ortalama olarak geçerlidir. bakınız.
Gözlemlenebilirlik parametreleri
Kurallara uygun konuşulduğunda, formüldeki ne v ne de Ddoğrudan gözlenebilir, çünkü onlar şimdi bir galaksinin özellikleridir; oysaki gözlemlerimiz geçmişteki galaksiyi kastedmektedir, bu zamanda biz ışığın bıraktıklarını görmekteyiz.
Göreceli olarak yakın galaksiler (kırmızıya kayma z bütünlükten daha azdır) için, v ve D çok değişmeyecektir ve v, 
Uzak galaksiler için, v (veya D) H’nin zamanla nasıl değiştiğini gösteren ayrıntılı bir model belirlemeden z’den hesaplanamaz. Kırmızıya kayma ışığın gösterdiği zamanda durgun hızla doğrudan bağlantılı değildir, fakat basit bir yoruma sahiptir: foton gözlemciye doğru hareket ederken, (1+z) evrenin genişleme faktörüdür.
Genişleme hızına göre görecelik hızı
Mesafeleri belirlemek için kullanılan Hubble kanununda, evrenin genişlemesinden ötürü sadece hız kullanılabilmektedir. Kütleçekimsel olarak etkileşen galaksiler evrenin büyümesinden bağımsız birbirine göre hareket ederler; bu göreceli hızlar özgün hızlar olarak adlandırılır veHubble kanununun uygulaması için hesaba katılması gerekir.
bu olgunun tek sonucudur. Galaksiler veya planet sistemleri gibi kütleçekime bağlı sistemlerde, uzay genişlemesi yerçekimi çekim kuvvetinden daha zayıf etkiye sahiptir.
İdeal Hubble Kanunu
Düzenli olarak genişleyen bir evren için ideal Hubble kanununun matematiksel türevi, 3 boyutlu Cartesian/Newtonian koordinat düzleminin epey basit geometrik bir teorisidir. Metrik uzay olarak düşünülür ve tamamen homojen ve izotropiktir (yer ve yön ile değişmeyen özellikler). Basitçe bu teoride anlatılır:
- Orjinden uzaklaşan herhangi iki nokta, her biri doğrusal çizgide ve orjinden uzaklığı orantılı bir hıza sahip olarak, birbirlerinden uzaklıklarına göre orantılı bir hızla uzaklaşırlar.
Yerel olarak homojen ve izotropik oldukları sürece Cartesian olmayan uzaya uygulanırlarsa; negatif ve pozitif eğri uzayların sıklıkla kozmolojik modeller oldukları düşünülür. ( bakınız)
Bu teoriden türeyen bir gözlem dünya üzerinde bizden uzaklaşan nesnelerdir ve dünyanın, genişlemenin olduğu bir merkeze yakın olduğunu gösterir, fakat genişleyen evrende her gözlemciden çok onlardan uzaklaşan nesneler görülür.
Nihai yazgı ve evrenin yaşı

Hubble parametresinin değeri 
Yavaşlama parametresinin 0’a eşit olduğu bir evrende, t Big Bang’den geçen zamandır ve H = 1/t ‘u izler. Sıfır olmayan zamana bağlı 
Uzun süre 
Olber paradoksu
Hubble kanununun Big Bang yorumunda özetlenen uzayın genişlemesi eskiden bilinen Olber paradoksu bilmecesiyle alakalıdır: eğer evren sonsuz, statik ve düzenli yıldız dağılımına sahipse, gökyüsündeki her çizgi bir yıldızla biterdi ve gökyüzü bir yıldız yüzeyinin parlaklığı gibi bir parlaklığa sahip olurdu. Ancak, gece gökyüzü karanlıktır. 17 yy.’dan bu yana astronomlar ve diğer düşünürler bu paradoksu çözmenin yollarını aradılar, fakat şu an kabul edilen çözüm Big Bang’in ve Hubble genişlemesinin bir kısmına dayanmaktadır. Sonlu bir zamandan beri var olan evren içinde, sadece belirli bir sayıda yıldız ışığı bize ulaşma şansına sahiptir ve paradoks böylece çözülür. Buna ek olarak, genişleyen bir evrende, uzak nesneler bizden uzaklaşır ve kırmızıya kayması ve parlaklığı azalması için ışığın onlardan yayılmasına neden olur.
Boyutsuz Hubble parameteresi
Hubble sabitiyle çalışmek yerine, boyutsuz Hubbel parametresini tanımak yaygın bir uygulamadır, genellikle h ile ifade edilir ve Hubble parametresini H0 as h × 100 km −1 −1olarak yazmak içindir, tüm belirsiz göreceli H0değeri h üzerine gönderilir.
Hubble sabitini belirleme

Hubble sabiti değeri uzak galaksilerin kırmızıya kaymalarını ve daha sonra bu galaksilerin uzaklıklarını belirlemeyi öngörür (Hubble kanunu yerine diğer yöntem). Fiziksel varsayımlardaki belirsizlikler, Hubble sabitinin değişen tahminlerine neden olan aralıkları belirlemeyi kullanırlar.
Erken dönem ölçümleri ve tartışmacı yaklaşımlar
20. yüzyılın ikinci yarısında çoğunlukla, 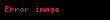
Bu önceki geniş farklılıklardaki tahminler, kısmen 1990’ların sonunda evrenin ΛCDM model girişi ile çözüldü. Sunyaev-Zel’dovich etkisini kullanan mikrodalga ve X-ray’de yüksek kırmızıya kayan kümelerin ΛCDM model gözlemleri ile, kozmik mikrodalga arka plan radyasyonunda anizotropların ölçümleri ve optik incelemelerin hepsi sabit için yaklaşık 70 değerini verdi.
Planck görevinden daha yakın ölçümler bu değeri 67 civarında gösteriyordu.
Günümüz ve geçmiş birçok ölçümün tablosuna bakınız.
Genişleme hızı
Tip Ia süpernovasının standart ışığından ölçülen bir 
Hubble parametresinin türevi
Friedmann denklemi ile başlayın:




Madde ve karanlık enerji baskın evren(Bir kozmolojik sabit ile)
Eğer evrende madde baskın ise, evrenin kütle yoğunluğu 
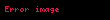

Yani, 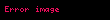
ve
Alt simge bugünkü değeri kastetmektedir ve 

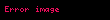
Madde ve karanlık enerji baskın evren
Eğer evren hem madde baskın hem karanlık enerji baskın ise, Hubble parametresi için yukarıdaki denklem karanlık enerjinin bir eşitlik durumu fonksiyonu olacaktır. Bu yüzden şimdi:

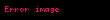
Eğer w sabitse,
Bu yüzden, sabit bir durum denklemi w ile karanlık enerji için w, 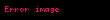
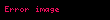
Eğer karanlık enerji sabit bir durum denklemine w sahip değilse,
Çözmek için denklemi parametikleştirdiğimizde,
Diğer bileşenler yeni formülleştirilmiştir. Yüksek enerji deneylerinin arka plan geometrisini belirleyen madde özelliklerinin analizinde güvenilir bir erişime sahip gözüktüğü belirli bir çağda, bu çağ derken quark-gluon plazma ve taşıyıcı özelliklerinin hesaba katıldığı bir çağdan bahsediyoruz. Bu sebeple, Hubble parametresinin evrimi ve diğer vazgeçilmez kozmolojik parametreleri böyle bir arka planda ideal evriminden farklı olduğu, gaz formunda, akışkan olmadığı bir arka plandan farklı olduğu düşünülür (göz ardı edilemez).
Hubble sabitinden türeyen birimler
Hubble zamanı
Hubble sabiti 

Biz şu an vakum enerjisinin baskınlığının artması yüzünden, üssel olarak büyüyen bir zaman dilimine yaklaşıyor gibi gözüküyoruz. Bu bağlamda, Hubble parametresi sabittir ve evren her Hubble zamanı için faktörü ile büyür:
Çok uzun zamanlardan sonra, dinamikler genel izafiyet, karanlık enerji, patlama ve buna benzer yukarıda açıklananlarla daha da karmaşıktır.
Hubble uzunluğu
Hubble uzunluğu ve Hubble hacmi kozlomoljide bir aralık birimidir, cH0−1 olarak tanımlanır – ışık hızı Hubble zamanıyla çarpılır. 4.228 milyon parsec veya 13.8 milyar ışık yılına eşittir. (Işık yılında Hubble uzunluğunun sayısal değeri tanım olarak Hubble zamanı yılına eşittir.) Hubble aralığı ışık hızında halen bizden uzaklaşan dünya ve galaksiler arasındaki bir mesafe olabilirdi, Hubble kanunu D = c/H0 için v = H0D çıkarılarak görülebilir.
Hubble hacmi
Hubble hacmi genellikle c/H0 boyutuyla birlikte hareket eden evrenin hacmi olarak tanımlanır. Gerçek tanım değişir: Genellikle çapı c/H0 olan bir küre hacmigibi tanımlanır, buna alternatif olarak küpün yüzeyi c/H0 da olabilir. The Hubble volume is sometimes defined as a volume of the Universe with a comoving size of Bazı kozmologlar hatta Hubble hacmi için çapının üç kat daha büyük olmasına rağmen gözlemlenebilir evrenin hacmi tanımını kullanırlar.
Ayrıca bakınız
Kaynakça
- ^ Isaacson, W. (2007). Einstein: His Life and Universe. . s. 354. ISBN . 26 Nisan 2014 tarihinde kaynağından . Erişim tarihi: 22 Mayıs 2015.
- ^ Dekel, A.; Ostriker, J. P. (1999). Formation of Structure in the Universe. Cambridge University Press. s. 164. ISBN .
- ^ Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. s. 58. ISBN .
- ^ Sartori, L. (1996). Understanding Relativity. University of California Press. s. 163, Appendix 5B. ISBN .
- ^ Sartori, L. (1996). Understanding Relativity. University of California Press. ss. 304-305. ISBN .
- ^ Chase, S. I.; Baez, J. C. (2004). . The Original Usenet Physics FAQ. 12 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Ekim 2013. See also Asimov, I. (1974). "The Black of Night". Asimov on Astronomy. . ISBN .
- ^ Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press.
- ^ Bucher, P. A. R.; et al. () (2013). "Planck 2013 results. I. Overview of products and scientific Results". Astronomy & Astrophysics. 571: A1. arXiv:1303.5062 $2. Bibcode:2014A&A...571A...1P. doi:10.1051/0004-6361/201321529.
- ^ Overbye, D. (1999). "Prologue". Lonely Hearts of the Cosmos (2. bas.). HarperCollins. s. 1ff. ISBN .
- ^ Perlmutter, S. (2003). "Supernovae, Dark Energy, and the Accelerating Universe" (PDF). . 56 (4). ss. 53-60. Bibcode:2003PhT....56d..53P. doi:10.1063/1.1580050. 4 Mart 2016 tarihinde kaynağından (PDF). Erişim tarihi: 22 Mayıs 2015.
- ^ Tawfik, A.; Harko, T. (2012). "Quark-hadron phase transitions in the viscous early universe". Physical Review D. 85 (8). s. 084032. arXiv:1108.5697 $2. Bibcode:2012PhRvD..85h4032T. doi:10.1103/PhysRevD.85.084032.
- ^ Tawfik, A. (2011). "The Hubble parameter in the early universe with viscous QCD matter and finite cosmological constant". Annalen der Physik. 523 (5). s. 423. arXiv:1102.2626 $2. Bibcode:2011AnP...523..423T. doi:10.1002/andp.201100038.
- ^ Tawfik, A.; Wahba, M.; Mansour, H.; Harko, T. (2011). "Viscous quark-gluon plasma in the early universe". Annalen der Physik. 523 (3). s. 194. arXiv:1001.2814 $2. Bibcode:2011AnP...523..194T. doi:10.1002/andp.201000052.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Hubble kanunu fiziksel kozmolojide gozlemlere verilen isimdir uzayin derinliklerinde gozlenen nesnelerin dunyadan uzak goreceli bir hizda yorumlanabilir bir Doppler kaymasina sahip oldugu bulunur ve dunyanin gerisinde kalan cesitli galaksilerin bu Doppler kaymasiyla olculen hizi yaklasik birkac yuz isik yili uzakligindaki galaksiler icin uzakliklariyla dogru orantilidir Bu normal olarak gozlemlenebilir evrenin uzaysal hacminin genislemesinin dogrudan bir gozlemi olarak yorumlanir Yalnizca bu genislemeden oturu olan astronomik nesnelerin devinimi Hubble akisi olarak bilinir Hubble kanunu genisleyen uzay paradigmasi icin gozlemlenebilen ilk temel olarak kabul edilir ve gunumuzde Big Bang modelinin desteklenmesi icin en cok atifta bulunulan kanitlarin parcalarindan biri olarak hizmet etmektedir Hubble kanunu nun genisleyen uzay paradigmasi icin gozlemlenebilir ilk temel oldugu bilinir ve bugun bu kanun Big Bang teorisi destegine atfedilen birkac parca kanittan birine hizmet eder Yaygin olarak Edwin Hubble a atfedilmesine ragmen kanun ilk 1927 de Georges Lemaitre tarafindan yayinlanan bir makalede genel izafiyet denklemlerinden turemistir Georges Lemaitre evrenin genisledigini one surmus ve bu genisleme orani icin tahmini bir deger vermistir bu deger su an Hubble sabiti olarak adlandirilir Edwin Hubble bu kanunun varligini onayladiktan iki yil sonra su an adiyla anilan sabit icin daha dogru bir deger belirlemistir Hubble nesnelerin durgun hizlari hakkinda onlarin kirmiziya kaymalarindan elde ettigi degerlerden bir cikarim yapmistir bu degerlerin bircogu daha onceleri olculmus ve 1917 yilinda Vesto Slipher tarafindan bulunan hizla iliskilendirilmistir Kanun genellikle su denklemle gosterilir v H0D H0 orantililik sabiti Hubble sabiti ile D zamani degistirebilir birlikte hareket ettigi araliga benzemez bir galaksiye uygun aralik arasi ve hizi v dir kozmolojik zaman koordinatina bagli olarak uygun araligin turevidir hiz in tanimi hakkindaki daha kurnaz tartismalar icin Uygun araligin kullanimlari na bakiniz H0 in SI birimi s 1 dir fakat daha siklikla km s Mpc den alintidir bir galaksinin km s icin hizina 1 isik yili 3 09 1019 km hizi verir H0 in karsiligi Hubble zamanidir Gozlemlenen degerlerYayimlanan tarih Hubble sabiti Gozlemci Uyarilar2016 11 22 71 9 2 4 3 0 Hubble Uzay Teleskobu Kutlecekimsel Merceklenme etkisi ile olusan birkac adet degisken isik kaynaginin fotograflari arasindaki zaman gecikmesi ile hesaplanmistir En guncel Hubble sabitidir 2016 07 13 67 6 0 7 0 6 Apache Noktasi Gozlemevi nin Sloan Digital Sky Survey Spektroskobu2016 05 17 73 00 1 75 Hubble Uzay Teleskobu Hubble Uzay Teleskobu nun Genis Alan Kamerasi kullanilarak tekrar olculmustur 2015 02 67 74 0 46 Planck Gorevi Planck Gorevi nin butun analizlerini iceren bilgiler 1 Aralik 2014 te Ferrara da yapilan konferansta halka acik bir sekilde paylasildi Gorevin detayli sonuclarini iceren dokumanlarin tamami ise Subat 2015 te yayinlandi 2013 03 21 67 80 0 77 Planck Gorevi Mayis 2009 da baslatildi Dort yillik bir zamandan sonra WMAP den daha kucuk bir aralikta CMB olcumu icin HEMT radyometreleri ve bolometri teknolojisini kullanan erken donem incelemeleri yerine daha onemli ayrintili incelemeler yapan kozmik mikrodalga radyasyonunu calistirmistir Planck kozmoloji aracinin arkasindaki Avrupalilar in basini cektigi arastirma takimi gorevin CMB tum gokyuzu haritasi ve onlarin belirledigi Hubble sabitinin de aralarinda bulundugu tum verilerini yayinlamistir 2012 12 20 69 32 0 80 WMAP 9 yillik Bu degerler WMAP ve diger kozmolojik verilerin birlesimi LCDM modelinin en basit surumune yerlestirilmesiyle ortaya cikmistir Eger veri daha genel surumlerle uyumluysa H0 degeri daha kucuk ve daha belirsiz olmaya yatkindir genellikle 67 4 km s Mpc civarindaysa da bazi modeller 63 km s Mpc civarinda deger verir 2010 71 0 2 5 WMAP 7 yillik 2010 70 1 1 3 WMAP 7 yillik 2009 02 70 1 1 3 WMAP 5 yillik 2009 02 71 9 2 6 2 7 WMAP 5 yillik 2006 08 77 6 14 9 12 5 Chandra X ray Gozlemevi2007 70 4 1 5 1 6 WMAP 3 yillik 2001 05 72 8 Hubble Uzay Teleskobu Bu proje en hassas optik belirlemeyi saglamis benzer dogruluga sahip bircok galaksi kumesinin Sunyaev Zel dovich etkisi gozlemlerine dayanandigindan uyumludur 1996 oncesi 50 90 tahmini 1958 75 tahmini Allan Sandage H0 icin ilki iyi tahmindi ama konsensusa varmadan once on yillik zaman gecebilirdi KesfiHubble gozlemlerini yapmadan yaklasik on yil once bircok fizikci ve matematikci Einstein in genel izafiyet alan denklemlerini kullanarak uzay ve zaman arasinda iliskili bir teori gelistirdiler Evrenin dogasinin en genel ilkelerini uygulayarak dinamik bir cozum uretildi fakat yaygin statik evren kavramiyla catismaktaydi FLRW denklemleri 922 de Alexander Friedmann evrenin olculebilir oranda genisleyebilecegini gosteren Einstein in alan denklemlerinden kendi Friedmann denklemlerini turetti Friedmann tarafindan kullanilan parametre bugun Hubble kanununun orantililik sabitinin bir aralik degiskeni gibi dusunuldugu bir aralik faktoru olarak bilinir Georges Lemaitre benzer bir cozumu 1927 de bagimsiz bir sekilde bulmustu Friedmann denklemleri yogunluk ve basinci verilen bir akiskan icin Einstein in alan denklemlerine homojen ve izotropik evren metrigi yerlesmesinden turetilir zaman fikri sonunda kozmolojinin Big Bang ve Kararli Hal teorilerine kilavuz oldu Lemaitre denklemi 1927 de Hubble makalesini yayinlamadan iki yil once Belcikali rahip ve astronom Georges Lemaitre Hubble Kanunu olarak bilinen arastirma turevlerini yayinlayan ilk kisiydi Maalesef bilinmeyen nedenlerden oturu radyal hizlar ve uzakliklara ve ilk basit H belirlenmesi dair tum arastirmasi ortadan kalkti Bu ihmallerin kasitli oldugu dusunulur Kanadali astronom Sidney van den Bergh e gore Evrenin genislemesine dair Lemaitre nin 1927 yilinda yaptigi kesif dusuk etkili bir Fransiz dergisinde yayinlandi 1931 de bu makalenin yuksek etkili Ingiliz tercumesinde kritik bir denklem su an Hubble sabiti olarak bilinen ortadan kaldirilan bir kaynak ile degistirildi Evrenin genislemesiyle ilgili bu makalenin o kismi bilinmeyen bir tercumanin ortadan kaldirmasinin onerildigi Ingiliz tercumesinden de silinmisti Evrenin sekli kesfinden once evrenin boyutu ve sekline dair konusmalar kayda degerdi 1920 de unlu Harlow Shapley ve Heber D Curtis arasinda gecti Shapley kucuk bir evrende boyutunu tartisirken Curtis evrenin daha buyuk oldugunu savundu Bu konu gelecek on yil icinde Hubble in gelistirdigi gozlemlerle cozulecekti Samanyolu icinde parlakligi zamanla degisen yildizlar Edward Hubble profesyonel astronomik gozlemci arastirmalarinin cogunu zamaninda dunyanin en guclu teleskoplariba sabit Mount Wilson Gozlemevi nde yapti parlakligi zamanla degisen yildizlar hakkindaki gozlemleri bu nesnelerin mesafesini hesaplamasinda olanak sagladi Surpriz bir sekilde bu nesneler Samanyolu disinda olduklari uzakliklarda kesfedildiler Bu nesnelere nebulalar denilmeye devam edildi ve yavas yavas galaksiler bu terimin yerini aldi Uzaklik olcumleriyle kirmiziya kayan degerleri birlestirme Hubble kanununa kirmiziya kayma degerleri uygun 30 Hubble sabiti icin cesitli tahminler vardir H0 71 2 H0 71 2 istatistiksel 6 sistematik km s 1Mpc 1 24 ve Sandage tarafindan H0 62 3 1 3 statistical 5 systematic km s 1Mpc 1 31 bulmak icin kirmiziya kayma degerleri 0 01 ve 0 1 arasinda anahtar grubuna uygundur Hubble kanununundaki parametreler hizlar ve araliklar dogrudan olculemez Gercekte bir mesafe ve kirmiziya kayma z l l radyasyonun spektrumu hakkinda bilgi verir Hubble parlaklik ve parametre z yi duzeltir Galaksi mesafe olcumlerinin Vesto Slipher ve Milton Humason kirmiziya kayma olcumleriyle birlesimi galaksilerle iliskilidir Hubble bir nesne ve onun uzakliginin kirmiziya kaymasi arasinda zor bir oranti kesfetti Dikkate deger bir dagilma ozgun hizlarin neden oldugu bilinir Hubble akisi durgun hizin ozgun hizlardan daha kucuk oldugu uzay alanindan cok uzak durumlari kasteder olmasina ragmen Hubble calistigi ve 500 km s Mpc Hubble sabitini uzaklik kalibrasyonlarindaki hatalardan dolayi su an kabul edilen degerden daha yuksek elde ettigi bir deger olan 46 galaksiden bir egilim cizgisi cizebildi ayrintilar icin kozmik aralik basamagina bakiniz Hubble kanununun kesfedildigi ve gelistirildigi zaman ozel gorecelilik anlaminda Doppler kaymasi gibi kirmiziya kayma olayini aciklamak kabul edilebilir hizla birlikte kirmiziya kaymayi iliskilendirmek icin Doppler formulunu kullanin Bugun Hubble kanununun hiz mesafe iliskisi Doppler etkisi degil evrenin genislemesine kozmolojik bir model sunan kirmiziya kayma ile baglantili ve hizla birlikte teorik bir sonuc olarak gorulmektedir Hubble kanununa giren kucuk z hizi icin kucuk z hizinda kirmiziya kayma iliskisi iki cikarim icin de ayni olmasina ragmen Doppler etkisi daha fazla yorumlanamaz Hubble diyagrami Hubble kanunu nesnenin hizinin gozlemciden uzakligina ortalama kirmiziya kayma degerleri ile orantili oldugu farzedilir gore cizildigi bir Hubble diyagraminda kolayca tarif edilebilir Bu diyagramda dogrusal cizginin pozitif egimi Hubble kanununun gorsel tasviridir Kullanilmayan kozmoloji sabiti Hubble in kesfi yayinlandiktan sonra Albert Einstein uzerine calismayi birakti duzenlemeyi dusundu Einstein genisleyen veya daralan bir evren icin en basit bicimde statik bir cozum yaratabildi Evrenin aslinda genisledigini gosteren Hubble in kesfinden sonra Einstein yanlis farz ettigi evrenin statik oldugu fikrini en buyuk hatasi olarak kabul etti Tek basina ele alindiginda deneylerle gozlemlenebilir ve orijinal olarak formullestirdigi denklemlerin ozel cozumlerini kullanarak teorik hesaplamalarini karsilastirabildigi buyuk kutlelerin isigi bukmesi veya Merkur gezegeninin devinimi gibi gozlemler boyunca genel izafiyet evrenin genislemesini ongorebilirdi 1931 de Einstein modern kozmolojide gozlemlenebilir bir temel saglayan Hubble a tesekkur etmek icin Mount Wilson a gitti Kozmoloji sabiti gecmis on yilda karanlik enerji icin bir hipotez olarak tekrar ilgi cekmeye basladi YorumOlasi durgun hiza basit dogrusal v cz bir iliski iceren kirmiziya kayma fonksiyonlarinin cesidi genel izafiyetle ilgili teorilerden olasi sekil cesitleri ve genel izafiyet ile uyumlu isiktan daha hizli hizlara izin vermeyen bir egri Tum egriler dusuk kirmiziya kaymalarda dogrusaldirlar Davis ve Lineweaver a bakiniz Kirmiziya kayma ve mesafe arasindaki dogrusal iliskinin kesfi durgun hiz ve asagidaki gibi Hubble kanunu icin basit bir matematiksel gosterim olusturan kirmiziya kayma arasindaki dogrusal hiz ile birlesir v H0D displaystyle v H 0 D burada v displaystyle v durgun hizdir km s olarak gosterilir H0 Hubble sabitidir ve altsimge 0 i simgeleyen alinan gozlem zamaninda Friedmann denklemleriyle uyumlu H displaystyle H ile gosterilir siklikla zamana bagli bir deger olan Hubble parametresidir ve aralik faktoru olarak ifade edilir D displaystyle D gozlemciden galaksiye uygun araliktir zamanla degisebilir sabit olan birlikte hareket mesafesine benzemez Durgun zaman v dD dt Hubble kanununun durgun hiz ve mesafe arasinda temel bir iliski olusturdugu dusunulur Ancak durgun hiz ve kirmiziya kayan degerler arasindaki iliski kabul edilmis kozmolojik modele baglidir ve kucuk kirmizi kaymalar disinda olusmaz Hubble kuresinin yaricapindan rHS daha buyuk mesafeler D icin nesneler isik hizindan daha hizli bir oranda uzaklasirlar Onemli bir tartisma icin Uygun Aralik Kullanimlari na bakiniz v dD dt Hubble sabiti zamanda degil sadece uzayda bir sabit oldugundan Hubble kuresinin yaricapi cesitli zaman araliklarinda artabilir ya da azalabilir Altsimge 0 bugunku Hubble sabitini gosterir Bugunku kanit evrenin hizlanan genislemesini Hizlanan evrene bakiniz one surmektedir yani herhangi bir galaksi icin durgun hiz dD dt galaksiler daha uzaga gittikce zamanla artmaktadir Ancak Hubble parametresinin aslinda zamanla azaldigi dusunulur Bu da eger bazi sabit uzakliktaki farkli galaksilere bakarsak ve onlari izlersek galaksilerin ayni uzakliktaki diger galaksilerden daha kucuk bir hizla gectigi anlamina gelirdi Kirmiziya kayma hizi ve durgun hiz Kirmiziya kayma uzak yildizsi gokcisimleri icin hidrojen a cizgileri gibi bilinen bir dalgaboyunu belirleyerek ve hareketli bir kaynakla karsilastirilan onemsiz bir kaymayi bularak olculebilir Bu kirmiziya kayma deneysel gozlemler icin kesin bir miktardir Kirmiziya kayma ve durgun hiz iliskisi diger bir maddedir Daha ayrintili tartisma icin Harrison a bakiniz Kirmiziya kayma hizi Kirmiziya kayma z genellikle kirmiziya kayma hizi olarak tanimlanir dogrusal bir Doppler etkisinden dolayi olsaydi durgun hiz ayni kirmizi kaymayi olusturabilirdi Evrenin kozmolojik genislemesinin neden oldugu kirmiziya kayma ayni durum degildir cunku hizlar Doppler kaymasinda goresiz bir formul kullanmak icin cok buyuktur Bu kirmiziya kayma hizi kolayca isik hizini asabilir Diger bir deyisle kirmiziya kayma hizini rHS belirlemedeki iliskide su vrs cz displaystyle v rs equiv cz kullanilir Yani kirmiziya kayma hizi ve kirmiziya kayma arasinda onemli bir fark yoktur kati bir sekilde birbiriyle orantilidir ve teorik nedenlere dayanmaz Kirmiziya kayma hizi terminolojisi otesindeki istek Fizeau Doppler formulunun dusuk bir hizla basitlestirilmesinden olusan kirmiziya kayma hiziyla uyumludur z lole 1 1 v c1 v c 1 vc displaystyle z frac lambda o lambda e 1 sqrt frac 1 v c 1 v c 1 approx frac v c lo le sirasiyla gozlemlenen ve gonderilen dalgaboylaridir Kirmiziya kayma hizi buyuk hizlarda gercek hizla ilgili degildir ancak bu terminoloji gercek hiz olarak yorumlanirsa bir karmasa yaratir Bir sonraki baslikta kirmiziya kayma veya kirmiziya kayma hizi ve durgun hiz arasindaki baglanti tartisilacaktir Bu tartisma Sartori ye dayanir Durgun hiz R t nin evrenin aralik faktoru oldugunu farzedin ve o secilen kozmolojik modele bagli olacak bir sekilde evrenin genislemesini arttirir Birlikte hareket eden noktalar arasinda olculen mesafelerin R yi orantili bir sekilde arttiracagi anlamina gelir Birlikte hareket eden noktalar uzayin genislemesinin bir sonucu olmasinin disinda birbirlerine gore goreceli olarak hareket etmez Diger bir deyisle D t D t0 R t R t0 displaystyle frac D t D t 0 frac R t R t 0 Eger isik te zamaninda bir galaksiden yansirsa ve biz onu t0 zamaninda alirsak evrenin genislemesinden dogan bir kirmizi kayma olusur ve bu kirmizi kayma z basitce soyledir z R t0 R te 1 displaystyle z frac R t 0 R t e 1 D mesafesinde bir galaksi farz edin ve bu mesafe belli oranda zamanla dtD degisir Bu durma oranina durgun hiz vr deriz vr dtD dtRRD displaystyle v r d t D frac d t R R D Hubble sabitini soyle tanimlariz H dtRR displaystyle H equiv frac d t R R Hubble kanunu soyle kesfederiz vr HD displaystyle v r HD Bu acidan Hubble kanunu i evrenin genislemesine katkida bulunan durgun hiz ve ii nesnenin uzakligi arasindaki temel baglantidir kirmiziya kayma ve mesafe arasindaki baglanti Hubble kanunu ile gozlemleri birbirine baglamak icin kullanilan bir destektir Bu kanun Taylor serisi genislemesi yapilarak ortalama bir sekilde kirmiziya kayma z ile iliskilendirilebilir z R t0 R te 1 R t0 R t0 1 te t0 H t0 1 t0 te H t0 displaystyle z frac R t 0 R t e 1 approx frac R t 0 R t 0 left 1 t e t 0 H t 0 right 1 approx t 0 t e H t 0 Eger mesafe cok buyuk degilse modelin diger tum zorluklari kucuk duzeltmeler olmaya baslar ve zaman araligi basitce araligin isik hizina bolunmesidir z t0 te H t0 DcH t0 displaystyle z approx t 0 t e H t 0 approx frac D c H t 0 or cz DH t0 vr displaystyle cz approx DH t 0 v r Bu yaklasima gore cz vr iliskisi modele bagli buyuk kirmiziya kaymalarla yer degistirmesi icin dusuk kirmiziya kaymalarda ortalama olarak gecerlidir bakiniz Gozlemlenebilirlik parametreleri Kurallara uygun konusuldugunda formuldeki ne v ne de Ddogrudan gozlenebilir cunku onlar simdi bir galaksinin ozellikleridir oysaki gozlemlerimiz gecmisteki galaksiyi kastedmektedir bu zamanda biz isigin biraktiklarini gormekteyiz Goreceli olarak yakin galaksiler kirmiziya kayma z butunlukten daha azdir icin v ve D cok degismeyecektir ve v v zc displaystyle v zc formulu kullanilarak tahmin edilebilir c isik hizidir Bu bize Hubble in buldugu basit formulu vermektedir Uzak galaksiler icin v veya D H nin zamanla nasil degistigini gosteren ayrintili bir model belirlemeden z den hesaplanamaz Kirmiziya kayma isigin gosterdigi zamanda durgun hizla dogrudan baglantili degildir fakat basit bir yoruma sahiptir foton gozlemciye dogru hareket ederken 1 z evrenin genisleme faktorudur Genisleme hizina gore gorecelik hizi Mesafeleri belirlemek icin kullanilan Hubble kanununda evrenin genislemesinden oturu sadece hiz kullanilabilmektedir Kutlecekimsel olarak etkilesen galaksiler evrenin buyumesinden bagimsiz birbirine gore hareket ederler bu goreceli hizlar ozgun hizlar olarak adlandirilir veHubble kanununun uygulamasi icin hesaba katilmasi gerekir bu olgunun tek sonucudur Galaksiler veya planet sistemleri gibi kutlecekime bagli sistemlerde uzay genislemesi yercekimi cekim kuvvetinden daha zayif etkiye sahiptir Ideal Hubble Kanunu Duzenli olarak genisleyen bir evren icin ideal Hubble kanununun matematiksel turevi 3 boyutlu Cartesian Newtonian koordinat duzleminin epey basit geometrik bir teorisidir Metrik uzay olarak dusunulur ve tamamen homojen ve izotropiktir yer ve yon ile degismeyen ozellikler Basitce bu teoride anlatilir Orjinden uzaklasan herhangi iki nokta her biri dogrusal cizgide ve orjinden uzakligi orantili bir hiza sahip olarak birbirlerinden uzakliklarina gore orantili bir hizla uzaklasirlar Yerel olarak homojen ve izotropik olduklari surece Cartesian olmayan uzaya uygulanirlarsa negatif ve pozitif egri uzaylarin siklikla kozmolojik modeller olduklari dusunulur bakiniz Bu teoriden tureyen bir gozlem dunya uzerinde bizden uzaklasan nesnelerdir ve dunyanin genislemenin oldugu bir merkeze yakin oldugunu gosterir fakat genisleyen evrende her gozlemciden cok onlardan uzaklasan nesneler gorulur Nihai yazgi ve evrenin yasi Evrenin yasi ve nihai yazgisi bugunku Hubble sabitinin olcumuyle belirlenebilir ve yavaslayan parametrenin gozlemlenen degerini tahmin eder yogunluk parametre degerleri ile karakterize edilirler WM madde icin ve WL karanlik enerji icin Kapali evren WM gt 1 ve WL 0 sonucu Buyuk Patlama ile son bulur ve onemli bir sekilde Hubble yasindan kucuktur Yasadigimiz WL sifir olmayan deger ile hizlanan evren icin evrenin yasi tesadufi olarak Hubble yasina yakindir Hubble parametresinin degeri q displaystyle q yavaslama parametresi olarak adlandirilan degerin artmasi veya azalmasi sonucu zamanla degisir soyle tanimlanir q 1 H H2 displaystyle q left 1 frac dot H H 2 right Yavaslama parametresinin 0 a esit oldugu bir evrende t Big Bang den gecen zamandir ve H 1 t u izler Sifir olmayan zamana bagli q displaystyle q degeri birlikte hareket eden ufkun boyutu 0 oldugunda o zamandan simdiki zamanimiza Friedmann denklemlerinin birlesimini icerir Uzun sure q displaystyle q nun kutlecekimsel etkiden oturu yavaslayan bir genislemeyi gosteren pozitif bir deger oldugu dusunuldu Evrenin yasinin 1 H den kucuk oldugunu ongoruyordu yaklasik 14 milyar yil Ornegin q of 1 2 gibi bir deger evrenin yasinin 2 3H oldugunu verirdi 1998 deki kesif q nun belirgin bir sekilde negatif anlami oldugunu ve evrenin aslinda 1 H degerinden daha buyuk oldugu anlamina gelmektedir Ancak evrenin yasina dair tahminler 1 H degerine cok yakindir Olber paradoksu Hubble kanununun Big Bang yorumunda ozetlenen uzayin genislemesi eskiden bilinen Olber paradoksu bilmecesiyle alakalidir eger evren sonsuz statik ve duzenli yildiz dagilimina sahipse gokyusundeki her cizgi bir yildizla biterdi ve gokyuzu bir yildiz yuzeyinin parlakligi gibi bir parlakliga sahip olurdu Ancak gece gokyuzu karanliktir 17 yy dan bu yana astronomlar ve diger dusunurler bu paradoksu cozmenin yollarini aradilar fakat su an kabul edilen cozum Big Bang in ve Hubble genislemesinin bir kismina dayanmaktadir Sonlu bir zamandan beri var olan evren icinde sadece belirli bir sayida yildiz isigi bize ulasma sansina sahiptir ve paradoks boylece cozulur Buna ek olarak genisleyen bir evrende uzak nesneler bizden uzaklasir ve kirmiziya kaymasi ve parlakligi azalmasi icin isigin onlardan yayilmasina neden olur Boyutsuz Hubble parameteresi Hubble sabitiyle calismek yerine boyutsuz Hubbel parametresini tanimak yaygin bir uygulamadir genellikle h ile ifade edilir ve Hubble parametresini H0 as h 100 km 1 1olarak yazmak icindir tum belirsiz goreceli H0degeri h uzerine gonderilir Hubble sabitini belirlemeSu anki arastirmalar icin belirsiz olcumleri iceren Hubble sabiti degeri Hubble sabiti degeri uzak galaksilerin kirmiziya kaymalarini ve daha sonra bu galaksilerin uzakliklarini belirlemeyi ongorur Hubble kanunu yerine diger yontem Fiziksel varsayimlardaki belirsizlikler Hubble sabitinin degisen tahminlerine neden olan araliklari belirlemeyi kullanirlar Erken donem olcumleri ve tartismaci yaklasimlar 20 yuzyilin ikinci yarisinda cogunlukla H0 displaystyle H 0 degeri 50 ve 90 km s Mpc arasinda tahmin ediliyordu Hubble sabitinin degeri bu degeri 100 olarak iddia eden ve bu degeri 50 olarak tahmin eden arasinda uzun ve bir nebze siddetli bir tartismanin konusu oldu Shapley Curtis tartismasina benzer bir iki degerin yaristigi tartisma 1996 da John Bahcall tarafindan yonetilen ve arasinda da gecti Bu onceki genis farkliliklardaki tahminler kismen 1990 larin sonunda evrenin LCDM model girisi ile cozuldu Sunyaev Zel dovich etkisini kullanan mikrodalga ve X ray de yuksek kirmiziya kayan kumelerin LCDM model gozlemleri ile kozmik mikrodalga arka plan radyasyonunda anizotroplarin olcumleri ve optik incelemelerin hepsi sabit icin yaklasik 70 degerini verdi Planck gorevinden daha yakin olcumler bu degeri 67 civarinda gosteriyordu Gunumuz ve gecmis bircok olcumun tablosuna bakiniz Genisleme hizi Tip Ia supernovasinin standart isigindan olculen bir q displaystyle q degeri 1998 de negatif olarak belirlendi ve bircok gok bilimci evrenin hizlanarak genisledigini gosteren bu bulgularla sok oldu Hubble faktoru hala zamanla azaliyor olmasina ragmen Yorum kisminda buraya deginilmistir karanlik enerji ve LCDM model makalelerine bakiniz Hubble parametresinin tureviFriedmann denklemi ile baslayin H2 a a 2 8pG3r kc2a2 Lc23 displaystyle H 2 equiv left frac dot a a right 2 frac 8 pi G 3 rho frac kc 2 a 2 frac Lambda c 2 3 H displaystyle H Hubble parametresi a displaystyle a aralik faktoru L displaystyle Lambda kozmolojik sabit G kutlecekim sabiti k displaystyle k evrenin normallesmis uzay egrisidir ve 1 0 or 1 e esittir Madde ve karanlik enerji baskin evren Bir kozmolojik sabit ile Eger evrende madde baskin ise evrenin kutle yogunlugu r displaystyle rho maddeyi iceren bir sekilde ele alinabilir r rm a rm0a3 displaystyle rho rho m a frac rho m 0 a 3 rm0 displaystyle rho m 0 maddenin bugunku yogunlugudur Gorecesiz parcaciklar icin kutle yogunlugunun evrenin hacmine ters bir sekilde orantili oldugunu biliyoruz bu yuzden yukaridaki denklem dogru olmalidir Hatta tanimlayabiliriz ne bakiniz Wm displaystyle Omega m rc 3H28pG displaystyle rho c frac 3H 2 8 pi G Wm rm0rc 8pG3H02rm0 displaystyle Omega m equiv frac rho m 0 rho c frac 8 pi G 3H 0 2 rho m 0 Yani r rcWm a3 displaystyle rho rho c Omega m a 3 Hatta tanimda Wk kc2 a0H0 2 displaystyle Omega k equiv frac kc 2 a 0 H 0 2 ve WL Lc23H02 displaystyle Omega Lambda equiv frac Lambda c 2 3H 0 2 Alt simge bugunku degeri kastetmektedir ve a0 1 displaystyle a 0 1 Friedmann denkleminde tum bunlari degistirirsek ve a displaystyle a ile a 1 1 z displaystyle a 1 1 z yi degistirirsek sunu elde ederiz H2 z H02 WM 1 z 3 Wk 1 z 2 WL displaystyle H 2 z H 0 2 left Omega M 1 z 3 Omega k 1 z 2 Omega Lambda right Madde ve karanlik enerji baskin evren Eger evren hem madde baskin hem karanlik enerji baskin ise Hubble parametresi icin yukaridaki denklem karanlik enerjinin bir esitlik durumu fonksiyonu olacaktir Bu yuzden simdi r rm a rde a displaystyle rho rho m a rho de a rde displaystyle rho de karanlik enerjinin kutle yogunlugudur Tanima gore rde a rde0a 3 1 w displaystyle rho de a rho de0 a 3 left 1 w right kozmolojide bir esitlik durumu dir ve bunu evrenin kutle yogunlugunun zamanla nasil degistigini tanimlayan akiskan denklemiyle degistirirsek ln r 3 1 w ln a displaystyle ln rho 3 left 1 w right ln a r a 3 1 w displaystyle rho a 3 left 1 w right Eger w sabitse rde a rde0e 3 daa 1 w a displaystyle rho de a rho de0 e 3 int frac da a left 1 w a right Bu yuzden sabit bir durum denklemi w ile karanlik enerji icin w rde a rde0a 3 1 w displaystyle rho de a rho de0 a 3 left 1 w right Eger bunu Friedmann denklemindeki gibi degistirirsek fakat uzaysal olarak duz bir yuzeyde yasadigimizi farzettigimiz k 0 displaystyle k 0 oldugu durumda H2 z H02 WM 1 z 3 Wde 1 z 3 1 w displaystyle H 2 z H 0 2 left Omega M 1 z 3 Omega de 1 z 3 left 1 w right right Eger karanlik enerji sabit bir durum denklemine w sahip degilse rde a rde0e 3 daa 1 w a displaystyle rho de a rho de0 e 3 int frac da a left 1 w a right Cozmek icin denklemi parametiklestirdigimizde H2 z H02 WMa 3 Wdea 3 1 w0 wa e 3wa 1 a displaystyle H 2 z H 0 2 left Omega M a 3 Omega de a 3 left 1 w 0 w a right e 3w a 1 a right Diger bilesenler yeni formullestirilmistir Yuksek enerji deneylerinin arka plan geometrisini belirleyen madde ozelliklerinin analizinde guvenilir bir erisime sahip gozuktugu belirli bir cagda bu cag derken quark gluon plazma ve tasiyici ozelliklerinin hesaba katildigi bir cagdan bahsediyoruz Bu sebeple Hubble parametresinin evrimi ve diger vazgecilmez kozmolojik parametreleri boyle bir arka planda ideal evriminden farkli oldugu gaz formunda akiskan olmadigi bir arka plandan farkli oldugu dusunulur goz ardi edilemez Hubble sabitinden tureyen birimlerHubble zamani Hubble sabiti H0 displaystyle H 0 ters zaman birimine sahiptir Ornegin 1H0 167 8km sMpc 4 55 1017s displaystyle 1 over H 0 1 over 67 8 textrm km sMpc 4 55 cdot 10 17 textrm s 14 4 milyar yil Bu evrenin 13 8 milyar yillik yasindan daha uzun bir zamandir Eger buyume dogrusal olsaydi Hubble zamani evrenin yasi olabilirdi buyume dogrusal olmadigi icin Hubble zamani evrenin gercek yasini vermez Biz su an vakum enerjisinin baskinliginin artmasi yuzunden ussel olarak buyuyen bir zaman dilimine yaklasiyor gibi gozukuyoruz Bu baglamda Hubble parametresi sabittir ve evren her Hubble zamani icin faktoru ile buyur H a a const a eHt et tH displaystyle H equiv frac dot a a textrm const Rightarrow a propto textrm e Ht textrm e t t H Cok uzun zamanlardan sonra dinamikler genel izafiyet karanlik enerji patlama ve buna benzer yukarida aciklananlarla daha da karmasiktir Hubble uzunlugu Hubble uzunlugu ve Hubble hacmi kozlomoljide bir aralik birimidir cH0 1 olarak tanimlanir isik hizi Hubble zamaniyla carpilir 4 228 milyon parsec veya 13 8 milyar isik yilina esittir Isik yilinda Hubble uzunlugunun sayisal degeri tanim olarak Hubble zamani yilina esittir Hubble araligi isik hizinda halen bizden uzaklasan dunya ve galaksiler arasindaki bir mesafe olabilirdi Hubble kanunu D c H0 icin v H0D cikarilarak gorulebilir Hubble hacmi Hubble hacmi genellikle c H0 boyutuyla birlikte hareket eden evrenin hacmi olarak tanimlanir Gercek tanim degisir Genellikle capi c H0 olan bir kure hacmigibi tanimlanir buna alternatif olarak kupun yuzeyi c H0 da olabilir The Hubble volume is sometimes defined as a volume of the Universe with a comoving size of Bazi kozmologlar hatta Hubble hacmi icin capinin uc kat daha buyuk olmasina ragmen gozlemlenebilir evrenin hacmi tanimini kullanirlar Ayrica bakinizKozmolojiKaynakca Isaacson W 2007 Einstein His Life and Universe Simon amp Schuster s 354 ISBN 0 7432 6473 8 26 Nisan 2014 tarihinde kaynagindan Erisim tarihi 22 Mayis 2015 Dekel A Ostriker J P 1999 Formation of Structure in the Universe Cambridge University Press s 164 ISBN 0 521 58632 1 Padmanabhan T 1993 Structure formation in the universe Cambridge University Press s 58 ISBN 0 521 42486 0 Sartori L 1996 Understanding Relativity University of California Press s 163 Appendix 5B ISBN 0 520 20029 2 Sartori L 1996 Understanding Relativity University of California Press ss 304 305 ISBN 0 520 20029 2 Chase S I Baez J C 2004 The Original Usenet Physics FAQ 12 Mayis 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 17 Ekim 2013 See also Asimov I 1974 The Black of Night Asimov on Astronomy ISBN 0 385 04111 X Peebles P J E 1993 Principles of Physical Cosmology Princeton University Press Bucher P A R et al 2013 Planck 2013 results I Overview of products and scientific Results Astronomy amp Astrophysics 571 A1 arXiv 1303 5062 2 Bibcode 2014A amp A 571A 1P doi 10 1051 0004 6361 201321529 Overbye D 1999 Prologue Lonely Hearts of the Cosmos 2 bas HarperCollins s 1ff ISBN 978 0 316 64896 7 Perlmutter S 2003 Supernovae Dark Energy and the Accelerating Universe PDF 56 4 ss 53 60 Bibcode 2003PhT 56d 53P doi 10 1063 1 1580050 4 Mart 2016 tarihinde kaynagindan PDF Erisim tarihi 22 Mayis 2015 Tawfik A Harko T 2012 Quark hadron phase transitions in the viscous early universe Physical Review D 85 8 s 084032 arXiv 1108 5697 2 Bibcode 2012PhRvD 85h4032T doi 10 1103 PhysRevD 85 084032 Tawfik A 2011 The Hubble parameter in the early universe with viscous QCD matter and finite cosmological constant Annalen der Physik 523 5 s 423 arXiv 1102 2626 2 Bibcode 2011AnP 523 423T doi 10 1002 andp 201100038 Tawfik A Wahba M Mansour H Harko T 2011 Viscous quark gluon plasma in the early universe Annalen der Physik 523 3 s 194 arXiv 1001 2814 2 Bibcode 2011AnP 523 194T doi 10 1002 andp 201000052
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State