Matematikte kök testi bir sonsuz serisinin yakınsaklığını belirlemek için kullanılan bir yöntemdir. Özellikle kuvvet serileriyle bağlantılı olarak yararlıdır.

Test
Kök testi ilk defa Cauchy tarafından geliştirilmiştir ve bu yüzden bazen Cauchy kök testi veya Cauchy radikal testi olarak da anılır. Kök testi
sayısını kullanır. Burada "lim sup", ∞ da olabilen üst (superior) limittir.
Kök testi şunu ifade etmektedir.
- C < 1 ise, seri mutlak yakınsaktır,
- C > 1 ise, seri ıraksaktır.
- C = 1 ise, test sonuçsuzdur.
Kuvvet serilerine uygulanması
Bu test, cn katsayılarının ve p merkezinin karmaşık sayı olduğu, z 'nin karmaşık değişken olduğu bir
kuvvet serisiyle kullanılabilir.
O zaman serinin terimleri an = cn(z - p)n ile verilir. O zaman kök testi an 'ye yukarıdaki gibi uygulanır. Bazen bu gibi bir seriye "p etrafındaki" kuvvet serisi adı verilir çünkü yakınsaklık yarıçapı R serinin iç bölgesindeki her z noktasında yakınsak olduğu en geniş p merkezli aralık veya diskin yarıçapıdır (aralığın veya diskin sınırı üzerindeki yakınsaklık ayrıca bakılmalıdır). Kök testinin böyle bir kuvvet serisine uygulanan bir sonucu ise yakınsaklık yarıçapının kesinlikle 
İspat
Σan serisinin yakınsaklığının kanıtı aslında karşılaştırma testinin bir uygulamasıdır. Her n ≥ N (n sabit bir doğal sayı) için 



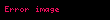
Sonsuz tane n için 
Sonucun kanıtı: Σan = Σcn(z - p)n kuvvet serisi için, serinin yakınsak olması için şunun olması gerektiğini görüyoruz:
Her n ≥ N için
ifadesine denk olarak
ifadesini sağlayan bir N vardır. Bu da serinin yakınsaması için yeteri kadar büyük n 'ler için 
demeye denktir. Böylece

olduğu zamandır (1'den büyük noktalarda ıraksaklık vardır) ve bu da yakınsaklık yarıçapını değiştirmeyecektir çünkü bunlar da aralığın veya diskin sınırının üzerinde yer alan noktalardır. Böylece
olur.
Ayrıca bakınız
Kaynakça
- Knopp, Konrad (1956), "3.2", Infinite Sequences and Series, Dover publications, Inc., New York,
- Whittaker, E. T., and Watson, G. N. (1963), "2.35", A Course in Modern Analysis (4 bas.), Cambridge University Press,
Bu makale PlanetMath'deki Cauchy kök testinin kanıtı maddesinden lisansıyla faydalanmaktadır.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte kok testi bir n 1 an textstyle sum n 1 infty a n sonsuz serisinin yakinsakligini belirlemek icin kullanilan bir yontemdir Ozellikle kuvvet serileriyle baglantili olarak yararlidir Kok testi icin karar akis diyagramiTestKok testi ilk defa Cauchy tarafindan gelistirilmistir ve bu yuzden bazen Cauchy kok testi veya Cauchy radikal testi olarak da anilir Kok testi C lim supn an n displaystyle C limsup n rightarrow infty sqrt n a n sayisini kullanir Burada lim sup da olabilen ust superior limittir Kok testi sunu ifade etmektedir C lt 1 ise seri mutlak yakinsaktir C gt 1 ise seri iraksaktir C 1 ise test sonucsuzdur Kuvvet serilerine uygulanmasiBu test cn katsayilarinin ve p merkezinin karmasik sayi oldugu z nin karmasik degisken oldugu bir f z n 0 cn z p n displaystyle f z sum n 0 infty c n z p n kuvvet serisiyle kullanilabilir O zaman serinin terimleri an cn z p n ile verilir O zaman kok testi an ye yukaridaki gibi uygulanir Bazen bu gibi bir seriye p etrafindaki kuvvet serisi adi verilir cunku yakinsaklik yaricapi R serinin ic bolgesindeki her z noktasinda yakinsak oldugu en genis p merkezli aralik veya diskin yaricapidir araligin veya diskin siniri uzerindeki yakinsaklik ayrica bakilmalidir Kok testinin boyle bir kuvvet serisine uygulanan bir sonucu ise yakinsaklik yaricapinin kesinlikle 1 lim supn cn n displaystyle 1 limsup n rightarrow infty sqrt n c n olmasidir Burada payda sifir olurken yaricapin olduguna dikkat edilmelidir IspatSan serisinin yakinsakliginin kaniti aslinda karsilastirma testinin bir uygulamasidir Her n N n sabit bir dogal sayi icin ann lt k lt 1 displaystyle sqrt n a n lt k lt 1 ise o zaman an lt kn lt 1 displaystyle a n lt k n lt 1 olur n N kn displaystyle sum n N infty k n geometrik serisi yakinsadigi icin o zaman karsilastirma testiyle n N an displaystyle sum n N infty a n de yakinsar Pozitif olmayan an icin yakinsaklik da an n displaystyle sqrt n a n kullanilarak ayni yolla kanitlanir Sonsuz tane n icin an n gt 1 displaystyle sqrt n a n gt 1 ise o zaman an 0 a yakinsamaz ve bu yuzden seri iraksak olur Sonucun kaniti San Scn z p n kuvvet serisi icin serinin yakinsak olmasi icin sunun olmasi gerektigini goruyoruz Her n N icin an n cn z p n n lt 1 displaystyle sqrt n a n sqrt n c n z p n lt 1 ifadesine denk olarak cn n z p lt 1 displaystyle sqrt n c n cdot z p lt 1 ifadesini saglayan bir N vardir Bu da serinin yakinsamasi icin yeteri kadar buyuk n ler icin z p lt 1 cn n displaystyle z p lt 1 sqrt n c n olmasini gerektirmektedir Bu da z p lt 1 lim supn cn n displaystyle z p lt 1 limsup n rightarrow infty sqrt n c n demeye denktir Boylece R 1 lim supn cn n displaystyle R geq 1 limsup n rightarrow infty sqrt n c n olur Simdi yakinsakligin mumkun oldugu tek yer an n cn z p n n 1 displaystyle sqrt n a n sqrt n c n z p n 1 oldugu zamandir 1 den buyuk noktalarda iraksaklik vardir ve bu da yakinsaklik yaricapini degistirmeyecektir cunku bunlar da araligin veya diskin sinirinin uzerinde yer alan noktalardir Boylece R 1 lim supn cn n displaystyle R 1 limsup n rightarrow infty sqrt n c n olur Ayrica bakinizOran testiKaynakcaKnopp Konrad 1956 3 2 Infinite Sequences and Series Dover publications Inc New York ISBN 0 486 60153 6 Whittaker E T and Watson G N 1963 2 35 A Course in Modern Analysis 4 bas Cambridge University Press ISBN 0 521 58807 3 KB1 bakim Birden fazla ad yazar listesi link Bu makale PlanetMath deki Cauchy kok testinin kaniti maddesinden GFDL lisansiyla faydalanmaktadir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State