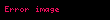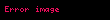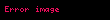Klein-Gordon Denklemi, (baz─▒ kaynaklarda Klein-Fock-Gordon E┼¤itli─¤i olarak da ifade edilir) Schr├Čdinger denkleminin ba─¤─▒l/g├Čreli (relativistik) olan versiyonudur ve atomalt─▒ fizikte kendi ekseni etraf─▒nda d├Čnmeyen par├¦ac─▒klar─▒ tan─▒mlamada kullan─▒l─▒r. ve taraf─▒ndan bulunmu┼¤tur.
Matematiksel A├¦─▒l─▒m
Serbest bir par├¦ac─▒k i├¦in Schr├Čdinger denklemi a┼¤a─¤─▒daki gibidir.
burada 
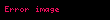
- Hamiltonyen i┼¤lemcisi (─ż);
Hamiltonyen i┼¤lemcisi, toplam enerjiyi karakterize eden ve i├¦inde (kinetik enerjiyi + potansiyel enerjiyi) bar─▒nd─▒ran bir operat├Črd├╝r.
Schr├Čdinger denklemi Einstein'─▒n ├¢zel G├Črelilik Kuram─▒'n─▒ hesaba katmad─▒─¤─▒ i├¦in ├Čzellikle atomalt─▒ par├¦ac─▒k hesaplamalar─▒nda yetersiz kal─▒r.
├¢zel G├Črelilik Kuram─▒'ndan enerjinin tan─▒m─▒n─▒ ihra├¦ edip
sonra, bu form├╝le kuantum mekanik ekledi─¤imizde,
sonucunu al─▒r─▒z. Ancak bu e┼¤itlik karek├Čkten dolay─▒ ve d├╝zensiz bir yap─▒dad─▒r ve bu y├╝zden Klein ve Gordon e┼¤itli─¤in daha objektif bir versiyonunu t├╝mdengelmi┼¤lerdir.
burada
ve
olur.
Bu yeni operat├Čre denir ve g├╝n├╝m├╝zde skaler (s─▒f─▒r rotasyonlu) par├¦ac─▒klar i├¦in olarak kullan─▒lmaktad─▒r.
G├Čreli serbest par├¦ac─▒k ├¦├Čz├╝m├╝
Serbest bir par├¦ac─▒─¤─▒n Klein-Gordon denklemi a┼¤a─¤─▒daki gibi yaz─▒labilir.
Yukar─▒daki ifadenin g├Čreli olmayan versiyonu ise bu ┼¤ekilde ifade edilebilir:
Ancak elbette bu durumda,
engeli olu┼¤acakt─▒r. G├Čreli olmayan par├¦ac─▒klarda oldu─¤u gibi, ayn─▒ ifadenin enerji ve momentum i├¦in olan versiyonlar─▒,
ve
┼¤eklinde form├╝le edilir. Bu noktada e┼¤itli─¤i k ve Žē bilinmeyenleri i├¦in ├¦├Čz├╝p yukar─▒da de─¤indi─¤imiz engel denklemine ihra├¦ etti─¤imizde m>0 k├╝tleli par├¦ac─▒klar─▒n enerji ve momentum de─¤erleri aras─▒ndaki ba─¤lant─▒y─▒ form├╝le etmi┼¤ oluruz.
K├╝tlesiz par├¦ac─▒klar i├¦in, yukar─▒daki denklemde m`i 0 olarak alabiliriz. Bu durumda k├╝tlesiz par├¦ac─▒─¤─▒n enerji ve momentumu aras─▒nda,
ili┼¤kisine ula┼¤─▒r─▒z.
Aksiyom
Klein-Gordon denklemi a┼¤a─¤─▒daki aksiyom kullan─▒larak t├╝mdengelinebilir.
burada 

Ayr─▒ca bak─▒n─▒z
- Dirac denklemi
- Kuantum alan kuram─▒
- Schr├Čdinger denklemi
- Klein-Gordon denkleminin matematiksel arg├╝manlar─▒ bu sayfada tart─▒┼¤─▒lm─▒┼¤t─▒: .
D─▒┼¤ ba─¤lant─▒lar
wikipedia, wiki, viki, vikipedia, oku, kitap, k├╝t├╝phane, k├╝t├╝bhane, ara, ara bul, bul, her┼¤ey, ne arasan─▒z burada,hikayeler, makale, kitaplar, ├Č─¤ren, wiki, bilgi, tarih, yukle, izle, telefon i├¦in, turk, t├╝rk, t├╝rk├¦e, turkce, nas─▒l yap─▒l─▒r, ne demek, nas─▒l, yapmak, yap─▒l─▒r, indir, ├╝cretsiz, ├╝cretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, m├╝zik, ┼¤ark─▒, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Klein Gordon Denklemi bazi kaynaklarda Klein Fock Gordon Esitligi olarak da ifade edilir Schrodinger denkleminin bagil goreli relativistik olan versiyonudur ve atomalti fizikte kendi ekseni etrafinda donmeyen parcaciklari tanimlamada kullanilir ve tarafindan bulunmustur Matematiksel AcilimSerbest bir parcacik icin Schrodinger denklemi asagidaki gibidir p22m Vps iŌäÅ tps displaystyle frac mathbf p 2 2m V psi i hbar frac partial partial t psi burada p iŌäÅ displaystyle mathbf p i hbar mathbf nabla displaystyle nabla ise Hamiltonyen islemcisi ─ż H p22m V displaystyle H frac mathbf p 2 2m V Hamiltonyen islemcisi toplam enerjiyi karakterize eden ve icinde kinetik enerjiyi potansiyel enerjiyi barindiran bir operatordur Schrodinger denklemi Einstein in Ozel Gorelilik Kurami ni hesaba katmadigi icin ozellikle atomalti parcacik hesaplamalarinda yetersiz kalir Ozel Gorelilik Kurami ndan enerjinin tanimini ihrac edip E p2c2 m2c4 displaystyle E sqrt mathbf p 2 c 2 m 2 c 4 sonra bu formule kuantum mekanik ekledigimizde iŌäÅ 2c2 m2c4ps iŌäÅ tps displaystyle sqrt i hbar mathbf nabla 2 c 2 m 2 c 4 psi i hbar frac partial partial t psi sonucunu aliriz Ancak bu esitlik karekokten dolayi ve duzensiz bir yapidadir ve bu yuzden Klein ve Gordon esitligin daha objektif bir versiyonunu tumdengelmislerdir 2 m2 ps 0 displaystyle Box 2 mu 2 psi 0 burada m mcŌäÅ displaystyle mu frac mc hbar ve 2 1c2 2 t2 2 displaystyle Box 2 frac 1 c 2 frac partial 2 partial t 2 nabla 2 olur Bu yeni operatore denir ve gunumuzde skaler sifir rotasyonlu parcaciklar icin olarak kullanilmaktadir Goreli serbest parcacik cozumuSerbest bir parcacigin Klein Gordon denklemi asagidaki gibi yazilabilir 2ps 1c2 2 t2ps m2c2ŌäÅ2ps displaystyle mathbf nabla 2 psi frac 1 c 2 frac partial 2 partial t 2 psi frac m 2 c 2 hbar 2 psi Yukaridaki ifadenin goreli olmayan versiyonu ise bu sekilde ifade edilebilir ps r t ei k r wt displaystyle psi mathbf r t e i mathbf k cdot mathbf r omega t Ancak elbette bu durumda k2 w2c2 m2c2ŌäÅ2 displaystyle k 2 frac omega 2 c 2 frac m 2 c 2 hbar 2 engeli olusacaktir Goreli olmayan parcaciklarda oldugu gibi ayni ifadenin enerji ve momentum icin olan versiyonlari p ps iŌäÅ ps ŌäÅk displaystyle langle mathbf p rangle langle psi i hbar mathbf nabla psi rangle hbar mathbf k ve E ps iŌäÅ t ps ŌäÅw displaystyle langle E rangle langle psi i hbar frac partial partial t psi rangle hbar omega seklinde formule edilir Bu noktada esitligi k ve w bilinmeyenleri icin cozup yukarida degindigimiz engel denklemine ihrac ettigimizde m gt 0 kutleli parcaciklarin enerji ve momentum degerleri arasindaki baglantiyi formule etmis oluruz E 2 m2c4 p 2c2 displaystyle left right langle E rangle 2 m 2 c 4 langle mathbf p rangle 2 c 2 Kutlesiz parcaciklar icin yukaridaki denklemde m i 0 olarak alabiliriz Bu durumda kutlesiz parcacigin enerji ve momentumu arasinda E p c displaystyle left right langle E rangle langle mathbf p rangle c iliskisine ulasiriz AksiyomKlein Gordon denklemi asagidaki aksiyom kullanilarak tumdengelinebilir S d4x 12 mŽĢ mŽĢ 12m2c2ŌäÅ2ŽĢ2 displaystyle mathcal S int mathrm d 4 x left frac 1 2 partial mu phi partial mu phi frac 1 2 frac m 2 c 2 hbar 2 phi 2 right burada ŽĢ displaystyle phi Klein Gordon alanini m displaystyle m ise kutleyi ifade etmektedir Ayrica bakinizDirac denklemi Kuantum alan kurami Schrodinger denklemi Klein Gordon denkleminin matematiksel argumanlari bu sayfada tartisilmisti Dis baglantilar PDF EqWorld Matematik Denklemleri Dunyasi Rusya 24 Mayis 2005 tarihinde kaynagindan PDF arsivlendi PDF EqWorld Matematik Denklemleri Dunyasi Rusya 24 Mayis 2005 tarihinde kaynagindan PDF arsivlendi PDF ABD 28 Eylul 2007 tarihinde kaynagindan PDF arsivlendi
 Azərbaycanca
Az╔Örbaycanca ąæąĄą╗ą░čĆčāčüą║č¢
ąæąĄą╗ą░čĆčāčüą║č¢ Dansk
Dansk Deutsch
Deutsch Espa├▒ola
Espa├▒ola Fran├¦ais
Fran├¦ais Indonesia
Indonesia Italiana
Italiana µŚźµ£¼Ķ¬×
µŚźµ£¼Ķ¬× ęÜą░ąĘą░ęø
ęÜą░ąĘą░ęø Lietuvos
Lietuvos Nederlands
Nederlands Português
Portugu├¬s ąĀčāčüčüą║ąĖą╣
ąĀčāčüčüą║ąĖą╣ ÓĘāÓĘÆÓČéÓĘäÓČĮ
ÓĘāÓĘÆÓČéÓĘäÓČĮ Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó
Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó T├╝rk├¦e
T├╝rk├¦e ąŻą║čĆą░茹Įčüčīą║ą░
ąŻą║čĆą░茹Įčüčīą║ą░ õĖŁÕ£ŗõ║║
õĖŁÕ£ŗõ║║ United State
United State Afrikaans
Afrikaans