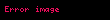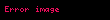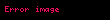Knudsen sayısı, moleküler ortalama serbest yol ile kabaca ölçülebilir uzunluk skalasının oranını veren boyutsuz sayıdır. Bu uzunluk skalası, örneğin, bir sıvının içinde yer alan bir cismin çapı olabilir. Knudsen sayısı adını Danimarkalı fizikçi Martin Knudsen'e (1871-1949) atfen almıştır.
Tanım
Knudsen sayısı aşağıdaki gibi tanımlanır:
= ortalama serbest yol [L1]
= kabaca ölçülebilir uzunluk skalası[L1].
Bir ideal gaz için ortalama serbest yol şu şekilde hesaplanabilir:
Boltzmann sabiti (1.3806504(24) × 10−23 J/K), [M1 L2 T−2 θ−1]
termodinamik sıcaklık, [θ1]
parçacık çapı, [L1]
toplam basınç, [M1 L−1 T−2].
Atmosfer içindeki parçaçık dinamiği için (standart basınç ve sıcaklık altında, 25 °C and 1 atm) ortalama serbest yol değeri aşağıdaki gibidir: 
Gazlarda Mach ve Reynolds sayıları ile ilişkisi
Knudsen sayısı Mach sayısı ve Reynolds sayısı ile ilişkilendirilebilir:
Ortalama molekül hızı (Maxwell-Boltzmann dağılımından),
dolayısıyla ortalama serbest yol,
herhangi bir uzunluk skalası L ile bölünürse Knudsen sayısı elde edilir:
ortalama moleküler hız (Maxwell–Boltzmann dağılımından), [L1 T−1]
- T termodinamik sıcaklık, [θ1]
- μ viskozite, [M1 L−1 T−1]
- m moleküler ağırlık, [M1]
- kB Boltzmann sabiti, [M1 L2 T−2 θ−1]
- ρ yoğunluk, [M1 L−3].
Boyutsuz Mach numarası:
Ses hızına aşağıdaki gibi ulaşılabilir:
- U∞ serbest akış hızı, [L1 T−1]
- R evrensel gaz sabiti, (8.314 47215 J K−1 mol−1), [M1 L2 T−2 θ−1 'mol'−1]
- M moleküler ağırlık, [M1 'mol'−1]
boyutsuz özgül ısılar oranı.
Boyutsuz Reynolds sayısı:
Mach sayısı Reynolds sayısına bölünürse,

Knudsen sayısı elde edilir.
Uygulaması
Knudsen sayısı, istatistiksel mekaniğin mi yoksa akışkanlar dinamiğinin sürekli ortamlar mekaniği formülasyonunun mu kullanılması gerektiğini belirlemede kullanılır:
Eğer ki Knudsen sayısı birim değere (b.b.d. 1) yakın ya da birim değerden fazlaysa, bir molekülün ortalama serbest yol değeri ilgili problemin uzunluk skalası ile yakın değerlerdedir demektir. Bu durumda, akışkanlar dinamiğinin sürekli ortamlar mekaniği varsayımı iyi bir varsayım olmaktan çıkar. Yerine istatistiksel mekanik formülasyonları kullanılmalıdır.
Yüksek değerli Knudsen sayısı problemleri atmosfer içindeki bir toz taneciğinin hareketi ya da bir uydunun eksosfer içindeki hareketi benzeri konuları içerir. Knudsen sayısı için en önemli işlev alanları mikroakışkan ve mikro elektro-mekanik sistemler tasarımı alanlarıdır.
Bir hava taşıtı etrafındaki akışa ait Knudsen sayısı düşüktür ve bu durum, bu ve buna benzer problemleri sürekli ortamlar mekaniği konusu haline getirir.
Knudsen sayısı, ayrıca, Stokes' yasasındaki Cunningham düzeltme faktöründe (küçük parçacıkların ilgili cisim üzerinde kayması nedeniyle oluşan sürükleme katsayısındaki değişiklik)(çapı dp < 5 µm'den ufak parçacıklar için) düzenleme yapmak için kullanılabilir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Knudsen sayisi molekuler ortalama serbest yol ile kabaca olculebilir uzunluk skalasinin oranini veren boyutsuz sayidir Bu uzunluk skalasi ornegin bir sivinin icinde yer alan bir cismin capi olabilir Knudsen sayisi adini Danimarkali fizikci Martin Knudsen e 1871 1949 atfen almistir TanimKnudsen sayisi asagidaki gibi tanimlanir Kn lL displaystyle mathit Kn frac lambda L l displaystyle lambda ortalama serbest yol L1 L displaystyle L kabaca olculebilir uzunluk skalasi L1 Bir ideal gaz icin ortalama serbest yol su sekilde hesaplanabilir Kn kBT2ps2pL displaystyle mathit Kn frac k B T sqrt 2 pi sigma 2 pL kB displaystyle k B Boltzmann sabiti 1 3806504 24 10 23 J K M1 L2 T 2 8 1 T displaystyle T termodinamik sicaklik 81 s displaystyle sigma parcacik capi L1 p displaystyle p toplam basinc M1 L 1 T 2 Atmosfer icindeki parcacik dinamigi icin standart basinc ve sicaklik altinda 25 C and 1 atm ortalama serbest yol degeri asagidaki gibidir l displaystyle lambda 8 10 8 m Gazlarda Mach ve Reynolds sayilari ile iliskisiKnudsen sayisi Mach sayisi ve Reynolds sayisi ile iliskilendirilebilir Dinamik viskozite m 12rc l displaystyle mu frac 1 2 rho bar c lambda Ortalama molekul hizi Maxwell Boltzmann dagilimindan c 8kBTpm displaystyle bar c sqrt frac 8k B T pi m dolayisiyla ortalama serbest yol l mrpm2kBT displaystyle lambda frac mu rho sqrt frac pi m 2k B T herhangi bir uzunluk skalasi L ile bolunurse Knudsen sayisi elde edilir lL mrLpm2kBT displaystyle frac lambda L frac mu rho L sqrt frac pi m 2k B T c displaystyle bar c ortalama molekuler hiz Maxwell Boltzmann dagilimindan L1 T 1 T termodinamik sicaklik 81 m viskozite M1 L 1 T 1 m molekuler agirlik M1 kB Boltzmann sabiti M1 L2 T 2 8 1 r yogunluk M1 L 3 Boyutsuz Mach numarasi Ma U cs displaystyle mathit Ma frac U infty c s Ses hizina asagidaki gibi ulasilabilir cs gRTM gkBTm displaystyle c s sqrt frac gamma RT M sqrt frac gamma k B T m U serbest akis hizi L1 T 1 R evrensel gaz sabiti 8 314 47215 J K 1 mol 1 M1 L2 T 2 8 1 mol 1 M molekuler agirlik M1 mol 1 g displaystyle gamma boyutsuz ozgul isilar orani Boyutsuz Reynolds sayisi Re rU Lm displaystyle mathit Re frac rho U infty L mu Mach sayisi Reynolds sayisina bolunurse MaRe U csrU L m mrLcs mrLgkBTm mrLmgkBT displaystyle frac Ma Re frac U infty div c s rho U infty L div mu frac mu rho Lc s frac mu rho L sqrt frac gamma k B T m frac mu rho L sqrt frac m gamma k B T gp2 displaystyle sqrt frac gamma pi 2 ifadesi ile carpilirsa mrLmgkBTgp2 mrLpm2kBT displaystyle frac mu rho L sqrt frac m gamma k B T sqrt frac gamma pi 2 frac mu rho L sqrt frac pi m 2k B T Kn kBT2ps2pL displaystyle mathit Kn frac k B T sqrt 2 pi sigma 2 pL Knudsen sayisi elde edilir UygulamasiKnudsen sayisi istatistiksel mekanigin mi yoksa akiskanlar dinamiginin surekli ortamlar mekanigi formulasyonunun mu kullanilmasi gerektigini belirlemede kullanilir Eger ki Knudsen sayisi birim degere b b d 1 yakin ya da birim degerden fazlaysa bir molekulun ortalama serbest yol degeri ilgili problemin uzunluk skalasi ile yakin degerlerdedir demektir Bu durumda akiskanlar dinamiginin surekli ortamlar mekanigi varsayimi iyi bir varsayim olmaktan cikar Yerine istatistiksel mekanik formulasyonlari kullanilmalidir Yuksek degerli Knudsen sayisi problemleri atmosfer icindeki bir toz taneciginin hareketi ya da bir uydunun eksosfer icindeki hareketi benzeri konulari icerir Knudsen sayisi icin en onemli islev alanlari mikroakiskan ve mikro elektro mekanik sistemler tasarimi alanlaridir Bir hava tasiti etrafindaki akisa ait Knudsen sayisi dusuktur ve bu durum bu ve buna benzer problemleri surekli ortamlar mekanigi konusu haline getirir Knudsen sayisi ayrica Stokes yasasindaki Cunningham duzeltme faktorunde kucuk parcaciklarin ilgili cisim uzerinde kaymasi nedeniyle olusan surukleme katsayisindaki degisiklik capi dp lt 5 µm den ufak parcaciklar icin duzenleme yapmak icin kullanilabilir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State