Kombinasyon, bir nesne grubu içerisinden sıra gözetmeksizin yapılan seçimlerdir. Nesne grubunun tekabül ettiği kümenin alt kümeleri olarak da tanımlanabilir. Çünkü alt kümelerde sıra önemli değildir.

Bir A kümesinin herhangi bir alt kümesine A kümesinin bir kombinasyonu denir. Mesela 52 iskambil kartı arasından seçilen dört kart, kartları seçme sırası önemli olmadığından bir kombinasyon problemidir.
Kombinasyon özellikleri
- C(R, 1) = R
- C(R, R) = 1
- C(R, 0) = 1
- N ≠ M olmak üzere C(R, N) = C(R, M) ise N + M = R
- C(R, N) = S (sayma sayıları) ise R, N'den küçük olamaz.
Kombinasyonların hesaplanması
n elemanlı bir kümeden seçilen r elemanlı kombinasyonların toplamı (n ≥ r olmak şartıyla) aşağıdaki formülle ifade edilir:
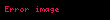
Kombinasyonun permütasyondan farkı, sıralamanın önemli olmamasıdır. Kombinasyonların toplamı, 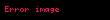
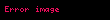

Örnek

 | C1 | C2 | C3 |
|---|---|---|---|
| R1 | 4 | 3 | 2 |
| R2 | 4 | 3 | 1 |
| R3 | 4 | 3 | 0 |
| R4 | 3 | 2 | 1 |
| R5 | 3 | 2 | 0 |
| R6 | 2 | 1 | 4 |
| R7 | 2 | 1 | 0 |
| R8 | 2 | 4 | 0 |
| R9 | 1 | 3 | 0 |
| R10 | 1 | 4 | 0 |
Ayrıca bakınız
Kaynakça
- ^ a b c . web.archive.org. 26 Ocak 2021. 26 Ocak 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Kasım 2021.
- ^ 10. Sınıf Matematik Akıllı Defter-1. Zafer ÖZLÜ, Mustafa Doğan. Eğitimiz Yayınları. 4 Ağustos 2021. ss. 14-21. 9 Ocak 2021 tarihinde kaynağından . Erişim tarihi: 7 Ocak 2021.
- ^ ARSLANTÜRK, BORA (7 Eylül 2014). SIFIRDAN MATEMATİK. Bora Arslantürk. s. 509. ISBN .
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kombinasyon bir nesne grubu icerisinden sira gozetmeksizin yapilan secimlerdir Nesne grubunun tekabul ettigi kumenin alt kumeleri olarak da tanimlanabilir Cunku alt kumelerde sira onemli degildir sanat ve tasarim kolektifi PHUNK tan sanat eseri Phiz Dingbats Bir A kumesinin herhangi bir alt kumesine A kumesinin bir kombinasyonu denir Mesela 52 iskambil karti arasindan secilen dort kart kartlari secme sirasi onemli olmadigindan bir kombinasyon problemidir Kombinasyon ozellikleriC R 1 R C R R 1 C R 0 1 N M olmak uzere C R N C R M ise N M R C R N S sayma sayilari ise R N den kucuk olamaz Kombinasyonlarin hesaplanmasin elemanli bir kumeden secilen r elemanli kombinasyonlarin toplami n r olmak sartiyla asagidaki formulle ifade edilir C n r nr nn r P n r r n r n r displaystyle C n r n choose r n choose n r frac P n r r frac n r n r Kombinasyonun permutasyondan farki siralamanin onemli olmamasidir Kombinasyonlarin toplami P n r displaystyle P n r permutasyonlarin toplami secilen elemanlarin kendi aralarindaki siralanma sayilarina r displaystyle r veya P r r displaystyle P r r bolunerek bulunabilir Ornek C 5 3 53 55 3 P 5 3 3 5 3 5 3 10 displaystyle C 5 3 5 choose 3 5 choose 5 3 frac P 5 3 3 frac 5 3 5 3 10 C 5 3 displaystyle C 5 3 C1 C2 C3R1 4 3 2R2 4 3 1R3 4 3 0R4 3 2 1R5 3 2 0R6 2 1 4R7 2 1 0R8 2 4 0R9 1 3 0R10 1 4 0Ayrica bakinizPermutasyonKaynakca a b c web archive org 26 Ocak 2021 26 Ocak 2021 tarihinde kaynagindan arsivlendi Erisim tarihi 6 Kasim 2021 10 Sinif Matematik Akilli Defter 1 Zafer OZLU Mustafa Dogan Egitimiz Yayinlari 4 Agustos 2021 ss 14 21 9 Ocak 2021 tarihinde kaynagindan Erisim tarihi 7 Ocak 2021 ARSLANTURK BORA 7 Eylul 2014 SIFIRDAN MATEMATIK Bora Arslanturk s 509 ISBN 978 605 88977 1 7 Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State