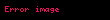Kosinüs teoremi, geometride, üçgen üzerinde iki kenarı ve aralarındaki açı verilmiş iken bilinmeyen kenarı bulmak amacıyla kullanılan formüldür. Şekil 1'deki üçgene göre kosinüs teoreminin uygulanışı şöyledir:

Kosinüs teoremi, iki kenar ve aralarındaki açı verildiğinde üçüncü kenarı bulmada ve üç kenar da verildiğinde açıları hesaplamada kullanılır. Ayrıca bu teorem, sadece dik üçgenlerde uygulanan Pisagor bağıntısını tüm üçgenler için geneller.
Kanıtlanması
Uzaklık Formülüyle
Kenarları 



Trigonometriyle

Şekil 2'deki gibi c kenarına bir dikme indirildiğinde dik üçgendeki trigonometrik bağıntılardan aşağıdaki bağıntı çıkar:
Her iki taraf c ile çarpıldığında ise:
Aynı bağıntılar diğer kenarlara dikme indirilerek düşünülürse:
bağıntıları bulunur. Her iki bağıntı alt alta toplanırsa aşağıdaki bağıntı ortaya çıkar:
En başta verilen bağıntıyla bağlantı kurmak için:
yapılır. Ardından en baştaki bağıntı en sondakine yazılırsa:
elde edilir.
İkizkenar üçgende kosinüs teoremi
Bir ikizkenar üçgende 

İlgili konular
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kosinus teoremi geometride ucgen uzerinde iki kenari ve aralarindaki aci verilmis iken bilinmeyen kenari bulmak amaciyla kullanilan formuldur Sekil 1 deki ucgene gore kosinus teoreminin uygulanisi soyledir Sekil 1 Acilari ve kenarlari isimlendirilmis bir ucgen a2 b2 c2 2bccos a displaystyle a 2 b 2 c 2 2bc cos alpha b2 a2 c2 2accos b displaystyle b 2 a 2 c 2 2ac cos beta c2 a2 b2 2abcos g displaystyle c 2 a 2 b 2 2ab cos gamma Kosinus teoremi iki kenar ve aralarindaki aci verildiginde ucuncu kenari bulmada ve uc kenar da verildiginde acilari hesaplamada kullanilir Ayrica bu teorem sadece dik ucgenlerde uygulanan Pisagor bagintisini tum ucgenler icin geneller KanitlanmasiUzaklik Formuluyle Kenarlari a b c displaystyle a b c ve c kenarinin karsisindaki acisi a displaystyle alpha olan bir ucgen dusunelim Bu ucgeni koordinat duzleminde A bsin a bcos a B 0 a C 0 0 displaystyle A b sin alpha b cos alpha B 0 a C 0 0 noktalariyla cizebiliriz Buradan da uzaklik formuluyle c bcos a a 2 bsin a 0 2 displaystyle c sqrt b cos alpha a 2 b sin alpha 0 2 bagintisi cikar Bu bagintidan hareketle asagidaki bicimde teorem kanitlanir c2 bcos a a 2 bsin a 0 2c2 b2cos2 a 2abcos a a2 b2sin2 ac2 a2 b2 sin2 a cos2 a 2abcos ac2 a2 b2 2abcos a displaystyle begin aligned c 2 amp b cos alpha a 2 b sin alpha 0 2 c 2 amp b 2 cos 2 alpha 2ab cos alpha a 2 b 2 sin 2 alpha c 2 amp a 2 b 2 sin 2 alpha cos 2 alpha 2ab cos alpha c 2 amp a 2 b 2 2ab cos alpha end aligned Trigonometriyle Sekil 2 Bir dikme indirilmis ucgen Sekil 2 deki gibi c kenarina bir dikme indirildiginde dik ucgendeki trigonometrik bagintilardan asagidaki baginti cikar c acos b bcos a displaystyle c a cos beta b cos alpha Her iki taraf c ile carpildiginda ise c2 accos b bccos a displaystyle c 2 ac cos beta bc cos alpha Ayni bagintilar diger kenarlara dikme indirilerek dusunulurse a2 accos b abcos g displaystyle a 2 ac cos beta ab cos gamma b2 bccos a abcos g displaystyle b 2 bc cos alpha ab cos gamma bagintilari bulunur Her iki baginti alt alta toplanirsa asagidaki baginti ortaya cikar a2 b2 accos b bccos a 2abcos g displaystyle a 2 b 2 ac cos beta bc cos alpha 2ab cos gamma En basta verilen bagintiyla baglanti kurmak icin accos b bccos a a2 b2 2abcos g displaystyle ac cos beta bc cos alpha a 2 b 2 2ab cos gamma yapilir Ardindan en bastaki baginti en sondakine yazilirsa c2 a2 b2 2abcos g displaystyle c 2 a 2 b 2 2ab cos gamma elde edilir Ikizkenar ucgende kosinus teoremiBir ikizkenar ucgende a b displaystyle a b ve iki esit kenar arasindaki aci g displaystyle gamma oldugu durumda c2 a2 b2 2abcos g displaystyle c 2 a 2 b 2 2ab cos gamma olan kosinus teoremi asagidaki sekli alir cos g 1 c22a2 displaystyle cos gamma 1 frac c 2 2a 2 Ilgili konularTrigonometri Kosinus Ucgen
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State