Köklü Sayı üssü reel olan herhangi bir sayının kök içine alınarak gösterilmesine denir. Her üslü sayı bir köklü sayıya dönüşebilmektedir ancak bu durum üssü olan sayılarda genellikle kullanılmaz zira Herhangi bir sayısının Şeklinde yazılması şeklinde yazılmasıyla aynı anlama gelmektedir.
Eğer bir sayının üssü tam sayıysa elde edilecek köklü sayı da tam sayıda bulunan gizli birden ötürü aynı anlama gelmektedir ve bu sayının kök içinde yazılması anlamsızdır ancak kökün kuvvetinde değişiklik yapılarak gösterim değiştirilebilir:
normalde yapılacak gösterim budur ancak kuvvetin olması bir anlam ifade etmeyeceğinden dolayı kökün kuvvetinde genişletme yapılır. Bu işlem şu şekilde gerçekleştirilir:
yapılan çarpım sonucu sayı bir nitelik kazanarak kuvvetiyle beraber köke girmeyi başarır. Eğer genişletirken kuvveti yapmak isteseydik sonuç şu olurdu:
Kuvveti iki olan sayılar karekök olarak adlandırılır ve kökün üstüne kuvvet yazılmaz. Kuvveti üç olan sayıların bir diğer ismi ise küpköktür.
Derece değiştirme
Bir sayının üssü o sayının kök içine nasıl alınacağını belirler. Böyle bir durumda üssün paydası kök içindeki sayının kuvvetini belirtir. Farklı kuvvetlere sahip köklü sayılarda işlem yapılabilmesi için kuvvetlerin eşitlenmesi gerekir. Üssü 



Bir sayının kuvvetinin değişmesi için o sayının istenilen kuvveti elde etmemizi sağlayacak bir sayıyla çarpılması gerekir. Kuvvet çarpıldığından dolayı kökün içindeki sayının üssü de aynı sayıyla çarpılır.
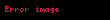


Sadeleştirme
Kök içindeki sayılar kuvvete bağlı olarak dışarıya çıkabilir,

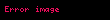
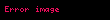


Dört İşlem
Çarpma
Temel çarpma hareketi uygulanır. Sayının katsayı kısımları kendi arasında kök kısımları kendi arasında çarpılır.

Eğer Köklerin kuvvetleri farklıysa Aşağıdaki işlemler yapılır.


Bölme
Temel bölme hareketi uygulanır. Sayının katsayı kısımları kendi arasında kök kısımları kendi arasında bölünür.

Eğer Köklerin kuvveti farklıysa aşağıdaki işlemler yapılır.


Toplama ve Çıkarma
Toplama ve çıkarma işlemlerinin yapılabilmesi için kök içindeki sayıların ve kuvvetlerin aynı olması gerekmektedir. Kökler aynı değilse sadeleştirilme yapılarak kökün dışına sayı çıkarılır. Dışarı çıkan katsayılar çıkarılır ya da toplanır.


İç İçe Kökler
Birbirinin içinde olan köklerin, kökün katsayısı olsun ya da olmasın kuvvetleri çarpılarak tek kök haline getirilebilir.
Eğer sadece en içteki kökte sayı varsa kuvvetlerin çarpılması yeterlidir.

Eğer en dıştaki kök haricinde her kökün 

En yaygın iç içe köklü ifadelerden biri :



Bu şekilde ayrılabilir.
İspat :
x ile y nin arasındaki işaret + olsun.




 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Koklu Sayi ussu reel olan herhangi bir sayinin kok icine alinarak gosterilmesine denir Her uslu sayi bir koklu sayiya donusebilmektedir ancak bu durum ussu 1 displaystyle 1 olan sayilarda genellikle kullanilmaz zira Herhangi bir a displaystyle a sayisinin a1 displaystyle a 1 Seklinde yazilmasi a1 displaystyle sqrt 1 a seklinde yazilmasiyla ayni anlama gelmektedir Eger bir sayinin ussu tam sayiysa elde edilecek koklu sayi da tam sayida bulunan gizli birden oturu ayni anlama gelmektedir ve bu sayinin kok icinde yazilmasi anlamsizdir ancak kokun kuvvetinde degisiklik yapilarak gosterim degistirilebilir 2 21 displaystyle 2 sqrt 1 2 normalde yapilacak gosterim budur ancak kuvvetin 1 displaystyle 1 olmasi bir anlam ifade etmeyeceginden dolayi kokun kuvvetinde genisletme yapilir Bu islem su sekilde gerceklestirilir 2 2n1 n displaystyle 2 sqrt 1 n 2 n yapilan carpim sonucu sayi bir nitelik kazanarak kuvvetiyle beraber koke girmeyi basarir Eger genisletirken kuvveti 2 displaystyle 2 yapmak isteseydik sonuc su olurdu 2 221 2 42 4 displaystyle 2 sqrt 1 2 2 2 sqrt 2 4 sqrt 4 Kuvveti iki olan sayilar karekok olarak adlandirilir ve kokun ustune kuvvet yazilmaz Kuvveti uc olan sayilarin bir diger ismi ise kupkoktur Derece degistirmeBir sayinin ussu o sayinin kok icine nasil alinacagini belirler Boyle bir durumda ussun paydasi kok icindeki sayinin kuvvetini belirtir Farkli kuvvetlere sahip koklu sayilarda islem yapilabilmesi icin kuvvetlerin esitlenmesi gerekir Ussu 1 b displaystyle 1 b olan herhangi bir a displaystyle a sayisi a1 b displaystyle a 1 b ve ab displaystyle sqrt b a ya esittir Bir sayinin kuvvetinin degismesi icin o sayinin istenilen kuvveti elde etmemizi saglayacak bir sayiyla carpilmasi gerekir Kuvvet carpildigindan dolayi kokun icindeki sayinin ussu de ayni sayiyla carpilir 523 displaystyle sqrt 3 5 2 sayisinin kuvveti 6 displaystyle 6 yapilmak istenirse 52 23 2 6256 displaystyle sqrt 3 2 5 2 2 sqrt 6 625 denilebilir SadelestirmeKok icindeki sayilar kuvvete bagli olarak disariya cikabilir 18 9 2 32 21 displaystyle sqrt 18 sqrt 9 2 sqrt 3 2 2 1 buradaki 32 displaystyle 3 2 sayisi kokun kuvveti 2 displaystyle 2 oldugundan dolayi disariya 3 displaystyle 3 olarak cikar yani sayi kokten cikarken ussunun paydasi kokun kuvvetiyle carpilmistir Bu da 3 2 displaystyle 3 sqrt 2 e esittir Kok disinda carpim haldeki bir sayinin koke alinmasi icin de bu islemin tersi yapilir Dort IslemCarpma Temel carpma hareketi uygulanir Sayinin katsayi kisimlari kendi arasinda kok kisimlari kendi arasinda carpilir 2 75 3 45 2 3 7 45 6285 displaystyle 2 sqrt 5 7 3 sqrt 5 4 2 3 sqrt 5 7 4 6 sqrt 5 28 Eger Koklerin kuvvetleri farkliysa Asagidaki islemler yapilir xn ym xmm n ynm n displaystyle sqrt n x sqrt m y sqrt m n x m sqrt m n y n 53 75 553 5 733 5 displaystyle sqrt 3 5 sqrt 5 7 sqrt 3 5 5 5 sqrt 3 5 7 3 Bolme Temel bolme hareketi uygulanir Sayinin katsayi kisimlari kendi arasinda kok kisimlari kendi arasinda bolunur 6 89 3 49 6 3 8 49 229 displaystyle 6 sqrt 9 8 3 sqrt 9 4 6 3 sqrt 9 8 4 2 sqrt 9 2 Eger Koklerin kuvveti farkliysa asagidaki islemler yapilir xn ym xmm n ynm n displaystyle sqrt n x sqrt m y sqrt m n x m sqrt m n y n 53 75 553 5 733 5 displaystyle sqrt 3 5 sqrt 5 7 sqrt 3 5 5 5 sqrt 3 5 7 3 Toplama ve Cikarma Toplama ve cikarma islemlerinin yapilabilmesi icin kok icindeki sayilarin ve kuvvetlerin ayni olmasi gerekmektedir Kokler ayni degilse sadelestirilme yapilarak kokun disina sayi cikarilir Disari cikan katsayilar cikarilir ya da toplanir 4 23 2 23 6 23 displaystyle 4 sqrt 3 2 2 sqrt 3 2 6 sqrt 3 2 4 23 2 23 2 23 displaystyle 4 sqrt 3 2 2 sqrt 3 2 2 sqrt 3 2 Ic Ice KoklerBirbirinin icinde olan koklerin kokun katsayisi olsun ya da olmasin kuvvetleri carpilarak tek kok haline getirilebilir Eger sadece en icteki kokte sayi varsa kuvvetlerin carpilmasi yeterlidir xnm xm n displaystyle sqrt m sqrt n x sqrt m n x Eger en distaki kok haricinde her kokun 1 displaystyle 1 den farkli bir katsayisi varsa butun katsayilar sirasiyla kendi icindeki koke girer en sonunda olusacak sayinin sadece en icteki kokunde bir sayi bulunacagindan kuvvetler carpilarak islem yapilir 2 543 24 543 8012 displaystyle sqrt 3 2 sqrt 4 5 sqrt 3 sqrt 4 2 4 5 sqrt 12 80 En yaygin ic ice koklu ifadelerden biri x m n displaystyle x m n ve y m n displaystyle y m n olmak uzere x 2y m n displaystyle sqrt x pm 2 sqrt y sqrt m pm sqrt n Bu sekilde ayrilabilir Ispat x ile y nin arasindaki isaret olsun x 2y displaystyle sqrt x 2 sqrt y m n 2m n displaystyle sqrt m n 2 sqrt m n m 2 n 2 2mn displaystyle sqrt sqrt m 2 sqrt n 2 2 sqrt m sqrt n m n 2 displaystyle sqrt sqrt m sqrt n 2 m n displaystyle sqrt m sqrt n Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

![{\displaystyle {\sqrt[{1}]{a}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4MllqQTVaalUyTnpjMFpUUXlOVFJoTVRNeE5qWmhOR1JpWWpjeFkySXdNMlE1WmpkaU1qWXouc3Zn.svg)
![{\displaystyle 2={\sqrt[{1}]{2}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5bE5HTTVNamcwTjJWbFpXRTVPRGN6WlRJMk5URXhaRGN5T1Rrd01HVXlaV1kyWTJJME56QXcuc3Zn.svg)
![{\displaystyle 2={\sqrt[{1.n}]{2^{n}}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4d01EWm1NRGxqTm1VeVpXSTJNalF6WkRZek56RXdNalkxWldZNU5URXlNR0UwTVdJek9ERXcuc3Zn.svg)
![{\displaystyle 2={\sqrt[{1.2}]{2^{2}}}={\sqrt[{2}]{4}}={\sqrt {4}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eE5tSm1ZamhqWXpKaE56ZzROak0xTTJWa05tRXdPV1EyWXpVeVpEY3pPVGRqWlRnME5UazIuc3Zn.svg)
