Kütle merkezi

Fizikte, uzaydaki ağırlığın dağılımının ağırlık merkezi, birbirlerine göre olan ağırlıkların toplamlarının sıfır olduğu noktadır. Ağırlık dağılımı, ağırlık merkezi etrafında dengelenir ve dağılan ağırlığın kütle pozisyon koordinatlarının ortalaması onun koordinatlarını tanımlar. Ağırlık merkezine göre formüle edildiği zaman mekanikte hesaplamalar basitleşir.

Çocuk baş parmağında oyuncağı dengede tutabilmek için kütle merkezi prensibinden yararlanmaktadır.

Deformasyonun yok sayıldığı cisimlerde durumunda, ağırlık merkezi sabitlenir ve eğer cismin değişmeyen bir yoğunluğu varsa, o zaman sentroidde yer alır. Ağırlık merkezi, boş veya nal gibi açık biçimli cisimlerde olduğu gibi, fiziksel cismin dışında da yer alabilir. Ayrı cisimlerin dağılımında, Güneş Sistemi'ndeki gezegenler gibi, ağırlık merkezi sistemin herhangi özel bir üyesinin pozisyonuyla bağdaştırılamaz.

Ağırlık merkezi uzayda kütlelerin dağılımını, gezegensel cisimlerin lineer ve açısal momentumu ve deformasyonun yok sayıldığı cisimlerin dinamiğinde, içeren mekanikteki hesaplamalar için yararlı bir referans noktasıdır. Yörüngesel mekanikte, gezegenlerin hareketlerinin denklemleri ağırlık merkezinde yer alan nokta kütleler olarak formüle edilir. Kütle çerçevesinin merkezi koordinat sisteminin orjinine göre geride kalan ağırlık merkezinin olduğu eylemsizlik çerçevesidir.

Tarih

“Ağırlık merkezi” tanımı ilk olarak eski Yunan fizikçi, matematikçi ve mühendis olan Arşimet tarafından kullanılmıştır. Yer çekimiyle ilgili varsayımları basitleştirmek için çalışmıştır. Sonuç olarak da şu an kullandığımız ağırlık merkezi denilen matematiksel özelliğe ulaşmıştır. Arşimet, kaldıraç üzerine kaldıraç boyunca değişik noktalardaki ağırlıklarla uygulanan torkun bütün kütlelerin tek bir noktaya - onların ağırlık merkezine - hareket ettirilmesiyle oluşacak kuvvetin aynı olacağını göstermiştir.

Euler'in ikinci kanununda yer alan ağırlık merkezine göre Newton'un ikinci kanunu tekrar formüle edilmiştir.

Kütle merkezine (C) P kuvvetiyle aşağıya çekilen cismin şeması

Tanım

Uzayda kütlelerin dağılımının merkezindeki tek nokta olan ağırlık merkezi, ağırlıkların bulunduğu pozisyonların vektörlerinin o noktaya göre toplamını sıfır olma özelliğine sahiptir. İstatistikte, ağırlık merkezi uzayda kütle dağılımının ortalamasıdır.

Parçacıkların sistemi (Pi)

R, ağırlık merkezinin koordinatları

r_i, yer aldıkları koordinatlar, i = 1,...,n

m_i, her birinin kütlesi, i = 1,...,n

${\displaystyle \sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )=0.}$

R için bu denklemi çözdüğümüzde, aşağıdaki formülü elde edilir:

${\displaystyle \mathbf {R} ={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\mathbf {r} _{i},}$

M bütün parçacıkların kütlelerinin toplamı.

Sürekli hacim

Eğer kütle dağılımı V hacminde ve ρ(r) yoğunluğunda sürekli ise, ağırlık merkezine, R, göre bu hacimdeki noktaların koordinatlarının integrali sıfıra eşittir.

${\displaystyle \int _{V}\rho (\mathbf {r} )(\mathbf {r} -\mathbf {R} )dV=0.}$

Bu denklemi R için çözersek, aşağıdaki denklem elde edilir:

${\displaystyle \mathbf {R} ={\frac {1}{M}}\int _{V}\rho (\mathbf {r} )\mathbf {r} dV,}$

M, bu hacimdeki toplam kütle

Eğer kütle dağılımı sabit bir yoğunluğa sahip ise, başka bir deyişle ρ sabit ise, hacmin sentroidi ile ağılık merkezi aynı olmuş olur. Ağırlık merkezi, düzlemdeki orta nokta demek değildir. İstatistikte, orta nokta ortalama ile aynı şey değildir.

Barycentric koordinatlar

İki parçacıklı sistemin, P1 ve P2, ağırlık merkezinin R koordinatları aşağıdaki gibi verilmiştir.

${\displaystyle \mathbf {R} ={\frac {1}{m_{1}+m_{2}}}(m_{1}\mathbf {r} _{1}+m_{2}\mathbf {r} _{2}).}$

m₁; birinci parçacığın kütlesi
m₂; ikinci parçacığın kütlesi

Toplam kütle yüzdesi, %100 P1 ve %0 P2'den %0 P1 ve %100 P2'ye göre değişiklik gösterdiğinde, kütle merkezi R P1 ve P2 arasında hareket eder. Her bir noktanın kütlesel yüzdesi o çizginin üzerinde bulunan R noktasının görüntü koordinatları diye gösterilebilir. Buna barycentric koordinatları diye adlandırılır. Bu yöntemi yorumlamanın diğer bir yolu ise göreli veriler hakkındaki momentlerin mekanik dengesidir. Bu sayı kütle merkezindeki toplam denge kuvvetiyle dengelenen toplam momenti verir. Bu, düzlemde ve uzaydaki görüntü koordinatlarını tanımlamak için sırasıyla üç nokta ve dört nokta ile genellenebilir.

Periyodik sınır şartları ile olan sistemler

Periyodik sınır şartlarıyla olan sistemlerdeki parçacıklar için, iki parçacık bu sistemin her iki karşı tarafında bulunmasına rağmen komşu olabilirler. Bu genellikle moleküler dinamik simülasyonlarında, örneğin rastgele pozisyonlarda çarpışmalarda veya bazen komşu atomlar periyodik sınırlarda kesiştiğinde meydana gelir. Çarpışmalar periyodik sınırlarla karşı karşıya kaldıklarında, kütle merkezinin hesaplanması yanlış olur. Periyodik sisitemler için kütle merkezinin hesaplanması için genellenmiş metot, düz çizgide çember varmış gibi her bir koordinatı, x ve y ve/veya z, işlemek içindir. Hesaplama her parçacığın x koordinatını alır ve bir açıya göre planlar.

${\displaystyle \theta _{i}={\frac {x_{i}}{x_{max}}}2\pi }$

x_max = x yönündeki sistem boyutu. Bu açı için, iki yeni nokta ${\displaystyle (\xi _{i},\zeta _{i})}$ genellenebilir:

${\displaystyle \xi _{i}=\cos(\theta _{i})}$

${\displaystyle \zeta _{i}=\sin(\theta _{i})}$

${\displaystyle (\xi ,\zeta )}$ düzleminde, bu koordinatlar yarıçapı 1 olan çember üstünde bulunurlar. Her parçacık için ${\displaystyle \xi _{i}}$ ve ${\displaystyle \zeta _{i}}$ değerlerinin toplamından, ortalama ${\displaystyle {\overline {\xi }}}$ ve ${\displaystyle {\overline {\zeta }}}$ hesaplanır. Bu değerler, kütle merkezinin x koordinatından elde edildiği yeni bir açı, ${\displaystyle {\overline {\theta }}}$, meydana getirir:

${\displaystyle {\overline {\theta }}=\mathrm {atan2} (-{\overline {\zeta }},-{\overline {\xi }})+\pi }$

${\displaystyle x_{com}=x_{max}{\frac {\overline {\theta }}{2\pi }}}$

Bu işlem tüm boyutlar için kütle merkezinin hesaplanması için tekrar edilir. Bu algoritma, tahmin etmek veya çarpışma analizini kullanarak periyodik sınırlardaki çarpışmaları “açmak” yerine, “en iyi” kütle merkezinin neresi olduğunu matematiksel olarak karar vermeye yardımcı olur. Eğer 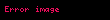${\displaystyle ({\overline {\xi }},{\overline {\zeta }})=(0,0)}$ olduğunda, ${\displaystyle {\overline {\theta }}}$ tanımlanamaz.Bu sonuç doğru çünkü sadece bütün parçacıklar kesin olarak uzayda olduğunda bu meydana gelir. Bu şartta, onların x koordinatı matematiksel olarak periyodik sistemde tanımlanır.

Kütleçekiminin merkezi

Kütleçekiminin merkezi kütleçekimi kuvvetinin sıfırlanmasından kaynaklanan net torkun olduğu cisimdeki bir noktadır. Kuvvet alanına dik şekilde hareket eden kütleçekiminin olduğu Dünya'nın yakınındaki yüzeyde, kütleçekimi merkezi ve herhangi bir cismin kütle merkezi aynıdır.

Uçakların, araçların ve gemilerin dinamiği ile ilgili çalışma, sistemin Dünya'nın yer çekimine yakın hareket ettiğini ve bunun sonucunda da yer çekimi merkezi ve kütle merkezi terimlerinin yer değiştirilebilir şekilde kullanılabilceğini farzetmektedir.

Fizikte, kütle dağılımının modelinde kullanılan kütle merkezinin yararları sürekli bir cismin net kütleçekimini hesaba katarak gözlemlenebilir. Cismin hacminin V, özkütlesinin de her r noktası için o hacimde ρ(r) olduğunu varsayın. Paralel kütleçekimi alanında kuvvet,

${\displaystyle \mathbf {f} (\mathbf {r} )=-dm\,g{\vec {k}}=-\rho (\mathbf {r} )dV\,g{\vec {k}},}$

d_m = r noktasındaki kütle
g = kütleçekimi ivmesi ve
k = dikey yönü tanımlayan vektör birimi

Bu hacimde R noktasını referansa noktası olarak seçin ve bu noktadaki net kuvvet ve torku hesaplayın,

${\displaystyle \mathbf {F} =\int _{V}\mathbf {f} (\mathbf {r} )=\int _{V}\rho (\mathbf {r} )dV(-g{\vec {k}})=-Mg{\vec {k}},}$

ve

${\displaystyle \mathbf {T} =\int _{V}(\mathbf {r} -\mathbf {R} )\times \mathbf {f} (\mathbf {r} )=\int _{V}(\mathbf {r} -\mathbf {R} )\times (-g\rho (\mathbf {r} )dV{\vec {k}})=\left(\int _{V}\rho (\mathbf {r} )(\mathbf {r} -\mathbf {R} )dV\right)\times (-g{\vec {k}}).}$

Eğer referans noktası kütle merkezi olacak şekilde R seçilirse,

${\displaystyle \int _{V}\rho (\mathbf {r} )(\mathbf {r} -\mathbf {R} )dV=0,}$

Net tork sıfıra eşit anlamındadır. Net tork sıfır olduğu için cisim, o cismin kütlesinin kütle merkezinde yoğunlaşmış gibi hareket edecektir.

Rijit cisim için kütleçekimi merkezi referans noktası olarak seçilerek, kütleçekimi kuvetleri cismin dönmesine neden olmayacak. Diğer bir deyişle, cismin ağırlığı kütle merkezinde yoğunlaşmış gibi düşünülebilir.

Lineer ve açısal momentum

Parçacıkların toplamının lineer ve açısal momentumu, kütle merkezine göre parçacıkların hızlarının ve pozisyonlarının ölçülmesiyle basitleştirilebilir. mi kütleli Pi, i=1,...,n parçacıkları ri koordinatlarında bulunuyorlar ve hızları da vi. R'yi referans noktası olarak seçtiğimizde hız ve pozisyon vektörlerini aşağıdaki gibi hesaplanır,

${\displaystyle \mathbf {r} _{i}=(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {R} ,\quad \mathbf {v} _{i}={\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {v} .}$

Referans noktası R'ye göre toplam lineer ve açısal momentum vektörleri

${\displaystyle \mathbf {p} ={\frac {d}{dt}}\left(\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\right)+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {v} ,}$

ve

${\displaystyle \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\left(\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\right)\times \mathbf {v} .}$

Eğer R noktası kütle merkezi olarak seçilirse, bu eşitlikler şu şekilde basitleştirilir,

${\displaystyle \mathbf {p} =m\mathbf {v} ,\quad \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} ),}$

m toplam kütle, p lineer momentum ve L açısal momentum.

Newton'un hareket kanunları, hiçbir dış kuvvetin olmadığı herhangi bir sistem için sabit bir momentuma ihtiyaç duyar. Diğer bir deyişle, kütle merkezi sabit hızla hareket eder. Bu klasik iç kuvvetler, manyetik alan, elektrik alanı, kimyasal reaksiyonlar vs ile birlikte olan bütün sistemler için uygulanır. Daha resmi şekilde, bu Newton'un üçüncü kanunu'na uyan herhangi bir iç kuvvet için doğrudur.

Kütle merkezini belirlemek

Plumb line metod

Bir cisim üstünde kütle merkezinin deneysel olarak bulunması cisim üzerindeki kütleçekimi kuvvetlerini kullanır ve Dünya'nın yüzeyine yakın bir yerde bulunan paralel kütleçekimindeki kütle merkezinin kütleçekimiyle aynı olduğu gerçeğine dayanır.

Simetri eksenine sahip ve sabit özkütleli cismin kütle merkezi mutlaka bu eksen üzerinde olmalıdır. Böylece, sabit yoğunluklu dairesel silindirin kütle merkezi, silindirin ekseni üzerinde onun kütle merkeziyle aynı yerdedir. Aynı şekilde, sabit özkütleli küresel simetrik cismin kütle merkezi kürenin merkezidir. Genel olarak, herhangi bir simetrik cisim için, onun kütle merkezi simetrinin sabit noktasıdır.

İki boyutlu cisimler

Kütle merkezini belirlemek için kullanılan deneysel metot, cismi iki noktadan uzaklaştırmak içindir ve bu uzaklaşmış noktaları çekül doğrusuna düşürmektir. Bu iki doğrunun kesiştiği yer kütle merkezidir.

Cismin şekli mutlaka matematiksel olarak önceden karar verilmiş olmalı, fakat bu bilinen bir formülü kullanmak için çok karmaşıktır. Bu durumda, bu karmaşık şekil kütle merkezinin kolay bulunabileceği daha basit şekillere bölünebilir. Eğer toplam kütle ve kütle merkezi her alan için bulunmuşsa, bütünün kütle merkezi bu merkezlerin ortalaması olur. Bu metot, negatif kütle olarak sayılan, boşlukları olan cisimler için bile kullanılabilir.

İntegerometre olarak da bilinen planimetrenin gelişimi, sentroidin veya standard olmayan iki boyutlu cismin kütle merkezini bulmak için kullanılabilir. Bu metot standard olmayan, yumuşak veya diğer metotların çok zor olduğu karmaşık sınırları olan cidimlere de uygulanabilir. Bu sıklıkla gemi yapımcıları tarafından gerekli yerdeğişimini ve suya batmamanın merkezini karşılaştırmak ve alabora olmasını engellemek için kullanılır.

Üç boyutlu cisimler

Üç boyutlu cisimlerin kütle merkezini deneysel olarak bulmak için kullanılan metot, cismin üç noktasından kütlenin ağırlığına; W= -Wk (k dikey yönün birim vektörü), karşı koyan F1, F2 ve F3 kuvvetlerini ölçerek başlar. r1, r2 ve r3'ü destek noktalarının pozisyon koordinatları olarak seçersek, kütle merkezinin R koordinatları net torkun sıfıra eşit olduğu şartı sağlarlar.

${\displaystyle \mathbf {T} =(\mathbf {r} _{1}-\mathbf {R} )\times \mathbf {F} _{1}+(\mathbf {r} _{2}-\mathbf {R} )\times \mathbf {F} _{2}+(\mathbf {r} _{3}-\mathbf {R} )\times \mathbf {F} _{3}=0,}$

ya da

${\displaystyle \mathbf {R} \times (-W{\vec {k}})=\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}.}$

Bu eşitlik, kütle merkezinin yatay düzlemdeki koordinatları olan R* verir.

${\displaystyle \mathbf {R} ^{*}={\frac {1}{W}}{\vec {k}}\times (\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}).}$

Kütle merkezi dikey çizgi L üzerindedir.

${\displaystyle L(t)=\mathbf {R} ^{*}+t{\vec {k}}.}$

Kütle merkezinin üç boyutlu koordinatları, bu kuvvetlerin cisimden geçen yatay iki düzlem için ölçülebilmesi için cisim ile iki kere deney yapılarak karar verilir. Kütle merkezi bu iki deneyden elde edilen L1 ve L2 çizgilerinin kesişimidir.

Uygulamaları

Kütle merkezi vücudun dışındadır.

Mühendisler kütle merkezi arabanın tutuşunu aşağıya çeksin diye spor arabaların tasarımında kullanırlar. Sırıksız yüksek atlama yapanlar, çubuğun üstünden rahat geçebilmek için kütle merkezinden yararlanırlar.

Astronomi

Kütle merkezi astronomide ve barycenter e karşılık gelen astrofizikte önemli bir rol oynar. Barycenter her iki cisminde dengede olduğu noktadır; iki veya daha fazla cismin birbirlerinin yörüngesinde döndüğü kütle merkezidir. Ay Dünya'nın yörüngesinde döndüğünde veya bir gezegen yıldızın etrafında döndüğünde, her iki cisim de büyük cismin merkezinden uzakta olan bir noktanın etrafında döner.

Havacılık

Kütle merkezi, uçakların dengesini etkileyen en önemli noktadır. Güvenli uçuş için yeterli bir dengeye ulaştığından emin olmak için, kütle merkezi mutlaka belirlenmiş limtilerin altında olmalıdır. Eğer kütle merkezi üst limitin üstündeyse, daha az manevra yapacaktır, böylece kalkarken veya havalanırken dönmesini zorlaştırır. Eğer kütle merkezi alt limitn altındaysa, bu sefer uçak fazla manevra yapacaktır ve uçmasını imkansızlaştıracak şekilde dengesiz olmasına neden olur. İrtifa dümeninin momenti, her zaman az olmalıdır. Aksi takdirde, stol şartlarından kurtulmasını zorlaşır.

Helikopetler için, kütle merkezi her zaman pervane noktasının hemen altında olmalıdır. İleri uçuşlarda, kütle merkezi, helikopteri ileriye iten dairesel kontrol uygulanarak üretilen negatif torku dengelemek için ileride olmalıdır.

İnşaat

Deprem yükleri, yapının rijitlik merkezine değil, kütle merkezine etkir. Bu nedenle kütle merkezinin de belirlenmesi gerekir. Kütle merkezinin hesabında, ağırlık merkezi ifadelerinden yararlanılabilir. Çünkü ağırlığın yer çekimi ivmesine bölünmesi ile kütle elde edilir ve yer çekimi; sisteme her noktada eşit miktarda etkir. Ancak burada asıl belirtilmesi gereken husus ağırlıkların belirlenmesinde sadece eleman ağırlıklarının değil diğer kalıcı ve dikkate alınması gerektiğidir. Ancak hareketli yükler belirli oranda azaltılarak hesaba dahil edilir. Çünkü bir sistemin her noktasının tamamen hareketli yükle dolu olduğunu göz önüne almak mantıksızdır.

Kütle merkezinin koordinatları (X_G,Y_G) aşağıdaki şekilde hesaplanır:

• ${\displaystyle X_{G}={\sum _{i=0}^{n}W_{i}*(e_{x})_{i}}/{\sum _{i=0}^{n}W_{i}}}$
• ${\displaystyle Y_{G}={\sum _{i=0}^{n}W_{i}*(e_{y})_{i}}/{\sum _{i=0}^{n}W_{i}}}$

${\displaystyle W_{i}}$=i. elemanın ağırlığı
${\displaystyle (e_{x})_{i}}$ = i. elemanın ağırlık merkezinin x koordinatı
${\displaystyle (e_{y})_{i}}$ = i. elemanın ağırlık merkezinin y koordinatı

Kinesiyoloji

Kinesiyolojide ve biyomekanikte kütle merkezi, insanın hareketini anlamaya yardımcı olan önemli bir parametredir. İnsan vücudunun kütle merkezi sabit bir şekle sahip olmadığı için sürekli değişir. İnsanın kütle merkezi reaksiyon kurulu ile veya hücre bölünmesiyle bulunur. Reaksiyon kurulu, reaksiyon kuruluna uzanan ve kütle merkezini bulmak için statik bir eşitlik kullanan statik bir analizdir. Hücre bölünmesi, aynı eksene göre bütün vücudun torkuna eşit olmak zorunda olan belli bir eksene göre vücudun bölümlerinin torklarının toplamını gösteren matematiksel çözümdür.