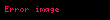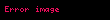Lagrange teoremi, grup teorisinde herhangi bir sonlu grubunun herhangi bir altgrubunun derecesinin (eleman sayısının) 'nin derecesini böldüğünü belirten bir teoremdir. Adını matematikçi Joseph-Louis Lagrange'dan almıştır.
Teoremin aşağıdaki hali bir altgrubu için sadece değil, ayrıca bu bölümün indisine de ('nin 'deki sol koset sayısına da) eşit olduğunu söyler.
Önerme
Teorem:
- Bir
grubunun her
altgrubu için
sağlanır.
Görüldüğü gibi teoremin bu hali 



Kanıt


ise bir
için
oluyorsa
ve
denk olsun.
Bu denklikten ötürü 
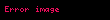





olur.
□
Kullanım Alanları
Lagrange teoreminin iddiası oldukça güçlüdür. Lagrange teoremi sayesinde, bir 
Lagrange teoremi, elemanların derecesi hakkında da bilgi verir. 





Ancak Lagrange teoremi, her bölen için bir altgrubun olması gerektiğini söylemez. Mesela 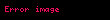
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
 | Cebir ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Lagrange teoremi grup teorisinde herhangi bir sonlu G displaystyle G grubunun herhangi bir altgrubunun derecesinin eleman sayisinin G displaystyle G nin derecesini boldugunu belirten bir teoremdir Adini matematikci Joseph Louis Lagrange dan almistir Teoremin asagidaki hali bir H lt G displaystyle H lt G altgrubu icin sadece G H N displaystyle G H in mathbb N degil ayrica bu bolumun G H displaystyle G H indisine de H displaystyle H nin G displaystyle G deki sol koset sayisina da esit oldugunu soyler OnermeTeorem Bir G displaystyle G grubunun her H displaystyle H altgrubu icin G G H H displaystyle G G H cdot H saglanir Goruldugu gibi teoremin bu hali G displaystyle G nin sonlu olmasini gerektirmez Cunku G H displaystyle G H G displaystyle G ve H displaystyle H kardinal sayilar olarak dusunulebilir KanitH displaystyle H nin sol kosetlerini soyle bir iliskiyle G displaystyle G nin icinde denklik siniflari olarak dusunebiliriz x y G displaystyle x y in G ise bir h H displaystyle h in H icin x hy displaystyle x hy oluyorsa x displaystyle x ve y displaystyle y denk olsun Bu denklikten oturu G displaystyle G yi ayrik aH displaystyle aH altgruplarinin birlesimi olarak yazabiliriz Bu a G displaystyle a in G larin sayisi ise H displaystyle H nin G displaystyle G deki sol kosetleri sayisidir G H displaystyle G H aH H displaystyle aH H oldugundan dolayi G G H H displaystyle G G H cdot H olur Kullanim AlanlariLagrange teoreminin iddiasi oldukca gucludur Lagrange teoremi sayesinde bir G displaystyle G grubunun altgruplarini cok daha hizli bir sekilde arayabiliriz Mesela bu teorem sayesinde 300 elemanli bir grubun icinde altgrup ararken 151 farkli eleman elde etmissek bu elemanlari kapsayan en kucuk altgrubun grubun kendisi oldugunu dogrudan soyleme sansi dogar Lagrange teoremi elemanlarin derecesi hakkinda da bilgi verir a displaystyle a bir grup elemani olsun a displaystyle langle a rangle nin eleman sayisi G displaystyle G nin eleman sayisini bolmek zorunda oldugundan a displaystyle a nin derecesinin de G displaystyle G yi boldugunu soylemek mumkundur Ayrica buna benzer bir mantikla bir grubun eleman sayisi asal ise a displaystyle langle a rangle nin tum grubu kapsamasi gerektigi sonucuna variriz Bunun sonucu olarak eleman sayisi asal olan tum gruplarin siklik dongusel oldugu ve hicbir bariz olmayan altgrubunun bulunmadigi ortaya cikar Ancak Lagrange teoremi her bolen icin bir altgrubun olmasi gerektigini soylemez Mesela A4 displaystyle A 4 un eleman sayisi 12 olsa da 6 elemanli hicbir altgrubu bulunmamaktadir Ayni zamanda bir bolen icin kac altgrubun bulundugunu da soylemez Ancak ve gibi daha zayif sartlar altinda altgruplarin var oldugunu iddia eden teoremler mevcutttur Matematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz Cebir ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State