Landau Kutbu veya diğer adıyla Moskova Sıfırı olarak bilinen, kuantum (nicem) alan kuramının sonsuz olduğu bağlaşım sabitindeki momentum (devinim) ölçeğidir. Bu olasılık Lev Landau ve meslektaşları tarafından belirtilmiştir. Bu bağlaşım sabiti, yeniden boylandırım grubun arkasında yatan temel fikirlerden olan momentum (devinim) ölçeğine dayanmaktadır.
Landau kutupları, kuantum elektrodinamik (QED) veya φ4 kuramı –dörtlenik sayısal alanla etkileşimi- gibi asimptotik kuramlarda görünür. Bu kuramlarda, yeniden boylandırım sabiti enerji ile büyür. Bir Landau kutbu, herhangi bir sonlu enerji ölçeğinde, bağlaşım sabiti sonsuz olduğunda ortaya çıkar. Bu durum kuramın tamamlanmış sayılabilmesinin önünde, matematiksel bir tutarsızlık olarak varsayılabilir. Muhtemel bir çözüm ise kesme (cut-off) kaldırıldığında yeniden boylandırım yükü sıfıra gidebilir. Bunun anlamı, yükün bütünüyle kuantum dalgalanması (vakum kutuplanması) ile taranmasıdır. Bu olay bir kuantum önemsizliğidir. Bunun anlamı, kuantum düzeltimleri kesmenin (cut-off) olmayışını tamamen bastırmaktadır.
Landau kutbu normalde bir ve iki döngülü pertübatif hesaplamalarla bulunur. Kutbun kuvvetli bağlaşımlarda pertübatif yaklaşıklığı bozması da olasıdır. Örgü alan kuramı, tedirginim kuramının da ötesinde kuantum alan kuramına cevaplar vermektedir. Bu çerçevede, sayısal hesaplamalar göstermiştir ki Landau’nun QED yükü sonsuz bir kesim (cut-off) için bütünüyle onaylanmaktadır.
Kısa Tarihçesi
Landau, Abrikosov ve Khalatnikov'a göre,
Bu formülde m parçacığın kütlesi ve Λ momentum (devinim) kesimidir. Sonlu g0 ve Λ → ∞ durumu için gözlemlenen gobs yükü sıfıra yakınsak olur ve kuram önemsiz görünür. Aslında, birinci denklemi ters çevirerek, g0 'ın gobs'un kesin bir değer olduğunu şu şekilde gösterebiliriz;


Bu aykırılık bir negatif artıklı Landau kutbudur. 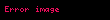






Eğer bu denklem tümleşik ise, 





Standart sınıflandırmaya göre, nitel olarak üç farklı durum söz konusudur:
(a) eğer 




(b) eğer 



(c) 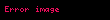




Landau ve c bendindeki olasılığı QED ve 










C bendindeki sav, olmayana ergi yönteminden anlaşılabildiği gibi bütün kuramdaki kuantum (nicem) önemsizliğine tekabül etmektedir. Doğrusu istenirse, eğer 


Olay Bilimsel Bakış Açıları
Bağlaşım sabitinin sıfır olmadığının bilindiği bir nokta ki fiziksel etkileşimleri göstermeye yönelik bir kuramda, Landau kutupları veya önemsizlik kuramındaki noksanlıkların belirtkesi olarak gözlenebilir. Örneğin QED'e kendi içinde tamamlanmış bir kuram olarak inanılmaz. Bir başka örnek ise Landau kutbu büyük birleşik kuramın içine yerleşerek giren yeni bir fizik olabilir. Büyük birleşik ölçek, Landau ölçeğinin altında, doğal bir kesim (cut-off) sağlayabilir.
QED'deki Landau kutbunun problemi saf akademik bir ilgi olmasıdır. Birinci ve ikinci denklemlerdeki 
Parçacık fiziğinin Standart Modeli'ndeki Higgs Bozonu, 
Son Gelişmeler
Landau kutbu çözümleri, rastgele bir 











Kaynakça
- ^ Lev Landau, Wolfgang Pauli (1955). Niels Bohr and the Development of Physics. Londra: Pergamon Press.
- ^ Göckeler, M. (1998). "Is There a Landau Pole Problem in QED?". Physical Review Letters. 80 (19). ss. 4119-4122. arXiv:hep-th/9712244 $2. Bibcode:1998PhRvL..80.4119G. doi:10.1103/PhysRevLett.80.4119.
- ^ S. Kim, John B. Kogut, Lombardo Maria Paola (31 Ocak 2002). "Gauged Nambu–Jona-Lasinio studies of the triviality of quantum electrodynamics". Physical Review D. 65 (5). s. 054015. arXiv:hep-lat/0112009 $2. Bibcode:2002PhRvD..65e4015K. doi:10.1103/PhysRevD.65.054015.
- ^ Gies, Holger; Jaeckel, Joerg (9 Eylül 2004). "Renormalization Flow of QED". Physical Review Letters. 93 (11). s. 110405. arXiv:hep-ph/0405183 $2. Bibcode:2004PhRvL..93k0405G. doi:10.1103/PhysRevLett.93.110405.
- ^ L. D. Landau, A. A. Abrikosov, and I. M. Khalatnikov, Dokl. Akad. Nauk SSSR 95, 497, 773, 1177 (1954).
- ^ Gell-Mann, M.; Low, F. E. (1954). "Quantum Electrodynamics at Small Distances". Physical Review. 95 (5). ss. 1300-1320. Bibcode:1954PhRv...95.1300G. doi:10.1103/PhysRev.95.1300.
- ^ N. N. Bogoliubov and D. V. Shirkov, Introduction to the Theory of Quantized Fields, 3rd ed. (Nauka, Moscow, 1976; Wiley, New York, 1980).
- ^ L.D.Landau, I.Ya.Pomeranchuk, Dokl. Akad. Nauk SSSR 102, 489 (1955); I.Ya.Pomeranchuk, Dokl. Akad. Nauk SSSR 103, 1005 (1955).
- ^ B.Freedman, P.Smolensky, D.Weingarten, Phys. Lett. B 113, 481 (1982).
- ^ Gunion, J.; H. E. Haber; G. L. Kane; S. Dawson (1990). The Higgs Hunters Guide. Addison-Wesley.
- ^ For example, Heller, Urs; Markus Klomfass; Herbert Neuberger; Pavols Vranas (20 Eylül 1993). "Numerical analysis of the Higgs mass triviality bound". Nuclear Physics B. 405 (2–3). ss. 555-573. arXiv:hep-ph/9303215 $2. Bibcode:1993NuPhB.405..555H. doi:10.1016/0550-3213(93)90559-8., which suggests MH < 710 GeV.
- ^ L.N.Lipatov, Zh.Eksp.Teor.Fiz. 72, 411 (1977) [Sov.Phys. JETP 45, 216 (1977)].
- ^ I. M. Suslov, JETP 107, 413 (2008); JETP 111, 450 (2010); http://arxiv.org/abs/1010.4081 25 Kasım 2018 tarihinde Wayback Machine sitesinde ., http://arxiv.org/abs/1010.4317 25 Kasım 2018 tarihinde Wayback Machine sitesinde ..
- ^ I. M. Suslov, JETP 108, 980 (2009), http://arxiv.org/abs/0804.2650 25 Kasım 2018 tarihinde Wayback Machine sitesinde ..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Landau Kutbu veya diger adiyla Moskova Sifiri olarak bilinen kuantum nicem alan kuraminin sonsuz oldugu baglasim sabitindeki momentum devinim olcegidir Bu olasilik Lev Landau ve meslektaslari tarafindan belirtilmistir Bu baglasim sabiti yeniden boylandirim grubun arkasinda yatan temel fikirlerden olan momentum devinim olcegine dayanmaktadir Landau kutuplari kuantum elektrodinamik QED veya f4 kurami dortlenik sayisal alanla etkilesimi gibi asimptotik kuramlarda gorunur Bu kuramlarda yeniden boylandirim sabiti enerji ile buyur Bir Landau kutbu herhangi bir sonlu enerji olceginde baglasim sabiti sonsuz oldugunda ortaya cikar Bu durum kuramin tamamlanmis sayilabilmesinin onunde matematiksel bir tutarsizlik olarak varsayilabilir Muhtemel bir cozum ise kesme cut off kaldirildiginda yeniden boylandirim yuku sifira gidebilir Bunun anlami yukun butunuyle kuantum dalgalanmasi vakum kutuplanmasi ile taranmasidir Bu olay bir kuantum onemsizligidir Bunun anlami kuantum duzeltimleri kesmenin cut off olmayisini tamamen bastirmaktadir Landau kutbu normalde bir ve iki dongulu pertubatif hesaplamalarla bulunur Kutbun kuvvetli baglasimlarda pertubatif yaklasikligi bozmasi da olasidir Orgu alan kurami tedirginim kuraminin da otesinde kuantum alan kuramina cevaplar vermektedir Bu cercevede sayisal hesaplamalar gostermistir ki Landau nun QED yuku sonsuz bir kesim cut off icin butunuyle onaylanmaktadir Kisa TarihcesiLandau Abrikosov ve Khalatnikov a gore L gt gt m displaystyle Lambda gt gt m oldugunda yeniden boylandirim kurami icin gozlenebilir gobs yuku ile ciplak g0 yuku arasindaki iliski izleyen formulle aciklanabilir gobs g01 b2g0ln L m 1 displaystyle g obs frac g 0 1 beta 2 g 0 ln Lambda m qquad qquad qquad 1 Bu formulde m parcacigin kutlesi ve L momentum devinim kesimidir Sonlu g0 ve L durumu icin gozlemlenen gobs yuku sifira yakinsak olur ve kuram onemsiz gorunur Aslinda birinci denklemi ters cevirerek g0 in gobs un kesin bir deger oldugunu su sekilde gosterebiliriz g0 gobs1 b2gobsln L m 2 displaystyle g 0 frac g obs 1 beta 2 g obs ln Lambda m qquad qquad qquad 2 L displaystyle Lambda buyurken ciplak yuk g0 g L displaystyle g 0 g Lambda da yeniden boylandirim noktasinda iraksanir Bu durumu formulize edersek LLandau mexp 1b2gobs 3 displaystyle Lambda Landau m exp left frac 1 beta 2 g obs right qquad qquad qquad 3 Bu aykirilik bir negatif artikli Landau kutbudur g L LLandau b2 L LLandau displaystyle g Lambda approx Lambda Landau beta 2 Lambda Lambda Landau Fakat aslinda g0 displaystyle g 0 in buyumesi g0 1 displaystyle g 0 approx 1 oldugu bolgede birinci ve ikinci denklemi gecersiz kilmaktadir Cunku bu denklemler g0 displaystyle g 0 in birden cok kucuk oldugu durumlarda elde edilmistir Dolayisiyla Landau kutbu nun kesin gercekligi kuskuludur g m displaystyle g mu yukunu m displaystyle mu momentum devinirlik olceginde bir islev olarak kabul ettigimizde bu yuk Gell Mann Low denklemiyle gosterilir dgdln m b g b2g2 b3g3 4 displaystyle frac dg d ln mu beta g beta 2 g 2 beta 3 g 3 ldots qquad qquad qquad 4 Eger bu denklem tumlesik ise g m gobs displaystyle g mu g obs m m displaystyle mu m ve g m g0 displaystyle g mu g 0 m l displaystyle mu lambda sartlari altinda birinci ve ikinci denklemleri saglamaktadir g m displaystyle g mu un genel tutumu b g displaystyle beta g islevinin gorunumune dayanir Standart siniflandirmaya gore nitel olarak uc farkli durum soz konusudur a eger b g displaystyle beta g nin sonlu g displaystyle g degerinde bir sifir varsa g displaystyle g nin buyumesi sature olmustur doygundur Ornek olarak g m g displaystyle g mu to g icin m displaystyle mu to infty b eger b g displaystyle beta g dalgali degil ise ve a 1 displaystyle alpha leq 1 durumunda ise b g ga displaystyle beta g propto g alpha gibi davraniyorsa g m displaystyle g mu nun buyumesi sonsuza devam eder c a gt 1 displaystyle alpha gt 1 durumunda eger b g ga displaystyle beta g propto g alpha buyuk g icin ise sonlu bir m0 degerinde g m displaystyle g mu iraksak olur Ayrica gercek Landau kutbu ile ilgili su sonuca varilir m gt m0 displaystyle mu gt mu 0 durumunda g m displaystyle g mu nun belirsizliginden dolayi kuram icten tutarsiz olmaktadir Landau ve c bendindeki olasiligi QED ve ϕ4 displaystyle phi 4 kuraminda ispat etmeye calisti Sonuclarina gore birinci denklemdeki g0 displaystyle g 0 in buyumesi gozlenebilir gobs displaystyle g obs yukunun sabit bir sinira gittigini gostermistir ki bu durum g0 displaystyle g 0 a dayanmaktadir Ayni davranis ikinci dereceden terimleri cikartilmis fonksiyonel integral islevsel tumlev ile de elde edilebilir Eger ikinci dereceden terimlerin yoksayilmasi g0 1 displaystyle g 0 ll 1 durumu icin zaten gecerliyse g0 displaystyle g 0 icin kesinlikle gecerlidir Bu bize rastgele bir g0 displaystyle g 0 icin birinci denklemi kullanma nedenimizi gostermektedir Nicel seviyede bu yaklasimlarin gecerliligi b displaystyle beta fonksiyonunun islevinin ikinci dereceden olmadigi durumlar haric tutularak yapilmistir Butun bunlara ragmen bunlar niteliksel olarak dogru olabilir Dogrusunu soylemek gerekirse gobs const g0 displaystyle g obs const g 0 sonucu sadece g0 1 displaystyle g 0 gg 1 durumunda fonksiyonel integral islevsel tumlev ile elde edilebilir g0 1 displaystyle g 0 approx 1 durumunda bu sonuc muhtemelen ihlal edilmistir ama buyukluklerine gore ele alinan iki sabitin rastlantisi ancak eslestirme kosulunda beklenebilir sonuclari Landau Pomeranchuk savini dogruluyor gorunmektedir C bendindeki sav olmayana ergi yonteminden anlasilabildigi gibi butun kuramdaki kuantum nicem onemsizligine tekabul etmektedir Dogrusu istenirse eger gobs displaystyle g obs sonlu ise bu kuram icten tutarsiz olmaktadir Bundan kacmanin tek yolu ise m0 displaystyle mu 0 sonsuzmus gibi davranmaktir Unutulmamalidir ki bu ancak gobs 0 displaystyle g obs to 0 durumunda mumkundur Cok yaygin bir fikir olarak hem QED hem de ϕ4 displaystyle phi 4 kurami surem sinirinda onemsizdir Aslinda mevcut bilgiler sadece g 0 durumunda b g nin pozitifligi ile ayni hesaba gelen Wilson Onemsizligini dogrulamaktadir Kuantum nicem onemsizliginin dogru belirtileri sayisiz degildir ve farkli yorumlara izin verir Olay Bilimsel Bakis AcilariBaglasim sabitinin sifir olmadiginin bilindigi bir nokta ki fiziksel etkilesimleri gostermeye yonelik bir kuramda Landau kutuplari veya onemsizlik kuramindaki noksanliklarin belirtkesi olarak gozlenebilir Ornegin QED e kendi icinde tamamlanmis bir kuram olarak inanilmaz Bir baska ornek ise Landau kutbu buyuk birlesik kuramin icine yerleserek giren yeni bir fizik olabilir Buyuk birlesik olcek Landau olceginin altinda dogal bir kesim cut off saglayabilir QED deki Landau kutbunun problemi saf akademik bir ilgi olmasidir Birinci ve ikinci denklemlerdeki gobs displaystyle g obs un gorevi asiri ince yapi sabiti a 1 137 tarafindan yapilir ve QED icin Landau olcegi 1028 eV olarak tahmin edilmistir ki bu durum gozlenebilir fizikteki enerji olceklerinin cok ustundedir Karsilastirmak icin soyle bir ornek verilebilir Buyuk Hadron Carpistiricisi nda LHC elde edilen en yuksek enerji 1013 eV dur Diger bir ornek ise Planck olceginde ki bu olcekte kuantum kutlecekim kuvveti onemli hale gelir maksimum enerji 1028 eV dur Parcacik fiziginin Standart Modeli ndeki Higgs Bozonu ϕ4 displaystyle phi 4 kurami tarafindan tanimlanmistir Eger son soylenen bir Landau kutbuna sahip ise bu gercek Higgs kutlesinde bir onemsizlik bagi kurdurtabilir Bu bag yeni fizigin varsaydigi dorduncu dereceden baglasimin maksimum degerine bu deger henuz bilinmemektedir giris izni verdigi olcege dayanmaktadir Genis baglasimlar icin pertubatif olmayan yontemler gereklidir Orgu hesaplamalari da bu konuda kullanislidir Son GelismelerLandau kutbu cozumleri rastgele bir g displaystyle g de g displaystyle g to infty b g displaystyle beta g Gell Mann Low fonksiyonu islevi hesaplamalariyla cozmeyi gerektirir Bu problem oldukca zor ve uzun yillar umutsuz vaka olarak kabul edilmistir Diyagramli cizgisel hesaplamalar b2 b3 displaystyle beta 2 beta 3 ldots gibi az miktarda genisleme sabitine cevap bulabilmekte ki bu durum bize butun b displaystyle beta fonksiyonunu islevini arastirma imkani vermemektedir Bu islem sureci genis basamakli pertubatif kurami hesaplamalari icin gelistirilen Lipatov metodundan yonteminden sonra mumkun hale gelebilecektir b displaystyle beta fonksiyonunun islevi yeniden insa edilmesi konusundaki ilk deneme ϕ4 displaystyle phi 4 kuraminin onemsizligi ile sonuclanmistir Daha ileri toplam yontemleri b g g displaystyle beta g propto g asimptotik davranilindaki a displaystyle alpha ussunu vermistir b g g displaystyle beta g propto g hipotezi onsavi ϕ4 displaystyle phi 4 kurami ve QED icin daha yeni cozumsel bir sekilde onaylanmistir b g displaystyle beta g nin pozitifligi ile birlikte serilerin toplaminin ele alinmasiyla Bogoliubov ve Shirkov un b bendindeki siniflandirmasini vermektedir Sonuc olarak Landau kutbu adi gecen kuramlarda bulunmamaktadir Landau ve Pomeranchuk tarafindan onerilen ikinci dereceden terimlerin yok sayilmasi fikri henuz onaylanmamistir Kaynakca Lev Landau Wolfgang Pauli 1955 Niels Bohr and the Development of Physics Londra Pergamon Press Gockeler M 1998 Is There a Landau Pole Problem in QED Physical Review Letters 80 19 ss 4119 4122 arXiv hep th 9712244 2 Bibcode 1998PhRvL 80 4119G doi 10 1103 PhysRevLett 80 4119 S Kim John B Kogut Lombardo Maria Paola 31 Ocak 2002 Gauged Nambu Jona Lasinio studies of the triviality of quantum electrodynamics Physical Review D 65 5 s 054015 arXiv hep lat 0112009 2 Bibcode 2002PhRvD 65e4015K doi 10 1103 PhysRevD 65 054015 Gies Holger Jaeckel Joerg 9 Eylul 2004 Renormalization Flow of QED Physical Review Letters 93 11 s 110405 arXiv hep ph 0405183 2 Bibcode 2004PhRvL 93k0405G doi 10 1103 PhysRevLett 93 110405 L D Landau A A Abrikosov and I M Khalatnikov Dokl Akad Nauk SSSR 95 497 773 1177 1954 Gell Mann M Low F E 1954 Quantum Electrodynamics at Small Distances Physical Review 95 5 ss 1300 1320 Bibcode 1954PhRv 95 1300G doi 10 1103 PhysRev 95 1300 N N Bogoliubov and D V Shirkov Introduction to the Theory of Quantized Fields 3rd ed Nauka Moscow 1976 Wiley New York 1980 L D Landau I Ya Pomeranchuk Dokl Akad Nauk SSSR 102 489 1955 I Ya Pomeranchuk Dokl Akad Nauk SSSR 103 1005 1955 B Freedman P Smolensky D Weingarten Phys Lett B 113 481 1982 Gunion J H E Haber G L Kane S Dawson 1990 The Higgs Hunters Guide Addison Wesley For example Heller Urs Markus Klomfass Herbert Neuberger Pavols Vranas 20 Eylul 1993 Numerical analysis of the Higgs mass triviality bound Nuclear Physics B 405 2 3 ss 555 573 arXiv hep ph 9303215 2 Bibcode 1993NuPhB 405 555H doi 10 1016 0550 3213 93 90559 8 which suggests MH lt 710 GeV L N Lipatov Zh Eksp Teor Fiz 72 411 1977 Sov Phys JETP 45 216 1977 I M Suslov JETP 107 413 2008 JETP 111 450 2010 http arxiv org abs 1010 4081 25 Kasim 2018 tarihinde Wayback Machine sitesinde http arxiv org abs 1010 4317 25 Kasim 2018 tarihinde Wayback Machine sitesinde I M Suslov JETP 108 980 2009 http arxiv org abs 0804 2650 25 Kasim 2018 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State


