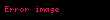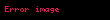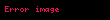Matematikte reel vektör uzayının f ile tanımlı pozitif değerler aldığı fonksiyon'un, eğer ise, logaritmik konveks veya süperkonveks olduğu söylenir.
Logaritmik konveks fonksiyon f, artan konveks fonksiyonu ile konveks fonksiyonunun bileşke fonksiyonu olduğundan konvekstir, ama tersi her zaman doğru değildir.
örneğin bir konveks fonksiyondur, ama konveks fonksiyon değildir ve böylece logaritmik konveks değildir. Diğer taraftan, konveks olduğundan logaritmik konvekstir. Gama fonksiyonuunun pozitif gerçel kısmı logaritmik konveks fonksiyona önemli bir örnektir. (bakınız Bohr-Mollerup teoremi).
Kaynakça
- ^ Kingman, J.F.C. 1961. A convexity property of positive matrices. Quart. J. Math. Oxford (2) 12,283-284.
- John B. Conway. Functions of One Complex Variable I, second edition. Springer-Verlag, 1995. .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte reel vektor uzayinin f ile tanimli pozitif degerler aldigi fonksiyon un eger log f displaystyle log f ise logaritmik konveks veya superkonveks oldugu soylenir Logaritmik konveks fonksiyon f artan exp displaystyle exp konveks fonksiyonu ile log f displaystyle log f konveks fonksiyonunun bileske fonksiyonu oldugundan konvekstir ama tersi her zaman dogru degildir ornegin f x x2 displaystyle f x x 2 bir konveks fonksiyondur ama log f x log x2 2log x displaystyle log f x log x 2 2 log x konveks fonksiyon degildir ve boylece f x x2 displaystyle f x x 2 logaritmik konveks degildir Diger taraftan log ex2 x2 displaystyle log e x 2 x 2 konveks oldugundan f x ex2 displaystyle f x e x 2 logaritmik konvekstir Gama fonksiyonuunun pozitif gercel kismi logaritmik konveks fonksiyona onemli bir ornektir bakiniz Bohr Mollerup teoremi Kaynakca Kingman J F C 1961 A convexity property of positive matrices Quart J Math Oxford 2 12 283 284 John B Conway Functions of One Complex Variable I second edition Springer Verlag 1995 ISBN 0 387 90328 3
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State