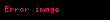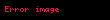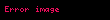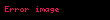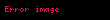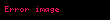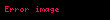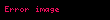Merkle-Hellman kripto sistemi, 1978 yılında Martin Hellman ve tarafından geliştirilen ilk açık anahtarlı kriptosistemlerden biridir.RSA'dan daha hızlı gerçekleştirilebilmesine rağmen Adi Shamir tarafından 1982'de güvensiz olduğu gösterilmiştir.
Tanım
Merkle-Hellman asimetrik anahtarlı bir kripto sistemdir; bunun anlamı, iletişim için iki anahtara ihtiyaç vardır. Bir Açık ve bir Gizli Anahtar. Ayrıca, RSA'dan farklı olarak, tek yönlüdür -Açık Anahtar sadece şifreleme ve Gizli Anahtar sadece deşifreleme için kullanılır. Böylece bu yöntem Dijital imzalama tarafından kimlik kanıtlama için kullanılamaz.
Merkle-Hellman sistemi altküme toplamı problemini (sırt çantası probleminin özel bir durumu) temel alır.Problem şu şekilde devam eder:
Belirlenmiş A kümesi ve bir b sayısı, b nin toplamlarından oluşan A nın bir altkümesi.Bununla birlikte eğer sayı kümesi ise -şöyle ki; sayı kümesinin her bir elemanı önceki sayıların tamamının toplamından daha büyük olmalı - problem ile beklenen zamanda ve kolayca çözülebilir.
Anahtar üretimi
Merkle-Hellman algoritmasında, anahtarlar birer sırt çantalarıdır. Açık anahtar A nın "kolayca kırılamayan" sırt çantasıdır ve Gizli Anahtar da B nin "basit" ya da süper artan bir sırt çantası, bir çarpan ve bir modülden oluşan iki ek sayının birleşimidir. Çarpan ve modül, süper artan sırt çantasından kolay kırılamayan sırt çantasına çevirmede kullanılabilir. Eğer, problem beklenen zamanda çözülebilirse; Aynı sayılar kolay kırılamayan sırt çantasının altküme toplamının basit sırt çantasının altküme toplamına çevrilmesinde kullanılabilir.
Şifreleme
Mesajı şifrelemek için; A'nın kolay kırılamayan sırt çantasının altkümesinden seçilen anahtar uzunluğunda bit kümesi ile karşılastırılır. Açık anahtardaki her bir terim, düz metindeki bir elemanı A_m altkümesinin bir elemanını karşılar, düz metindeki 0 A_m kümesinin inşa edilmesini göz ardı eder.Bu altkümenin elemanları toplanmış ve toplamanın sonucu şifrelenmiş metindir.
Deşifreleme
Deşifreleme mümkündür; çünkü çarpan ve modül kolayca çevrilebilir, süper artan sırt çantasındaki acık anahtar,böylece süper artan sırt çantasındaki elemanların karşılandığı toplamdaki şifreli metin sayı dönüştürme çevriminde kullanılabilir. Sonra; basit bir Greedy Algoritması kullanılarak, basit sırt çantası Büyük o gösterimindeki aritmetik operatörler kullanılarak çözülür. Böylece mesaj deşifrelenmiş olur.
Matematiksel metot
Anahtar üretimi
n bitten oluşan mesajı şifrelemek için süperartan bir dizi seçilir:
w = (w1, w2, ..., wn) n sıfırdan farklı doğal sayı.
q gibi bir rastgele sayı seçilir:
![image]() ve r gibi rastgele bir sayı seçilir:
ve r gibi rastgele bir sayı seçilir: Ortak bölen(r,q) = 1 (r ve q Aralarında asal)
q nun böyle seçilmesi şifrelenmiş metnin benzersiz olmasını sağlar. Eğer q düz metinden daha küçük seçilirse, aynı şifrelenmiş metinler elde edilebilir. r ile q aralarında asal olmalıdır yoksa mod q göre tersine çevrilemeyecektir. q nun tersinin olması gereklidir. Böylece deşifreleme yapılabilir.
Şimdi diziyi hesaplayalım:
β = (β1, β2, ..., βn)
βi = rwi mod q.
Açık Anahtar β ve Gizli Anahtarlar (w, q, r) dir.
Şifreleme
n bit mesajı şifrelemek için
- α = (α1, α2, ..., αn),
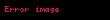
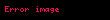
Şifrelenmiş metin c dir.
Deşifreleme
Deşifreleme amacıyla alınan bir c şifreli mesajı, 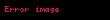
βi rastgele değerler aldığından dolayı bu zor bir problem olabilir. Çünkü alıcı alt küme probleminin örnek bir çözümüne sahip olmalıdır.
Anahtar Şifreleme, s tam sayılarını r mod q nun modüler tersinden bulmaktır. Bunun anlamı, s r mod q=1 den s yi ya da s'r=k'q+1 k gibi bir tam sayı bulmaktır. r, Ortak bölen(r,q) = 1 den seçildiğinden kullanılarak k ve s bulunabilir. Alıcı c şifreli metnini hesaplar:Bu yüzden
Çünkü rs mod q = 1 ve βi = rwi mod q
Bu yüzden
Bütün wi değerlerinin toplamı q dan küçüktür ve bu yüzden 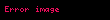
Örnek
İlk olarak süper artan bir dizi olan w yi oluşturalım:
- w = {2, 7, 11, 21, 42, 89, 180, 354}
Bu Gizli Anahtar için temeldir. Buradan toplamı hesaplayalım:
Sonra toplamdan büyük bir q sayısı seçelim:
q = 881
Ayrıca, 
r = 588- q, w ve r den oluşan Gizli anahtarımız oluşmuş oldu.
w kümesinin her bir elemanını rmodq ile çarparak β kümesini üretiyoruz:
- β = {295, 592, 301, 14, 28, 353, 120, 236}
Çünkü
2 * 588 mod 881 = 295 7 * 588 mod 881 = 592 11 * 588 mod 881 = 301 21 * 588 mod 881 = 14 42 * 588 mod 881 = 28 89 * 588 mod 881 = 353 180 * 588 mod 881 = 120 354 * 588 mod 881 = 236
β kümesi ile Açık Anahtarımızı oluşturmuş olduk.
Ayşe "a" yı şifrelemek istediğini söylesin. İlk önce Ayşe "a" nın ikili tabandaki değerini bulmalıdır (bu durumda, ASCII ya da UTF-8 kullanılmalıdır).
- 01100001
Ayşe sırasıyla her bir biti β kümesindeki eşleşen her bir elemanla çarpmalıdır.a = 01100001
0 * 295 + 1 * 592 + 1 * 301 + 0 * 14 + 0 * 28 + 0 * 353 + 0 * 120 + 1 * 236 = 1129
Bunu alıcıya göndermelidir. Ali, deşifrelerken bu sayıyı r −1 mod 
1129 * 442 mod 881 = 372
Şimdi Ali, 372 den; w kümesinden seçilen 372 ye eşit ya da 372 den küçük en büyük sayıyı çıkararak en son fark 
372 - 354 = 1818 - 11 = 77 - 7 = 0
Seçtiğimiz elemanların yerine 1 yazdığımızda ortaya gönderilen mesajın ikili karşılığı çıkmış olur.01100001
Bu ikili kod geri çevrildiğinde, Ayşe'nin Ali'ye yolladığı "a" mesajına ulaşmış oluruz.
Kaynakça
- ^ Merkle, Ralph; Hellman, Martin (1978). "Hiding information and signatures in trapdoor knapsacks". IEEE Transactions on Information Theory. 24 (5). ss. 525-530. doi:10.1109/TIT.1978.1055927.
- ^ Shamir, Adi (1984). "A polynomial-time algorithm for breaking the basic Merkle - Hellman cryptosystem". IEEE Transactions on Information Theory. 30 (5). ss. 699-704. doi:10.1109/SFCS.1982.5.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Merkle Hellman kripto sistemi 1978 yilinda Martin Hellman ve tarafindan gelistirilen ilk acik anahtarli kriptosistemlerden biridir RSA dan daha hizli gerceklestirilebilmesine ragmen Adi Shamir tarafindan 1982 de guvensiz oldugu gosterilmistir Tanim Merkle Hellman asimetrik anahtarli bir kripto sistemdir bunun anlami iletisim icin iki anahtara ihtiyac vardir Bir Acik ve bir Gizli Anahtar Ayrica RSA dan farkli olarak tek yonludur Acik Anahtar sadece sifreleme ve Gizli Anahtar sadece desifreleme icin kullanilir Boylece bu yontem Dijital imzalama tarafindan kimlik kanitlama icin kullanilamaz Merkle Hellman sistemi altkume toplami problemini sirt cantasi probleminin ozel bir durumu temel alir Problem su sekilde devam eder Belirlenmis A kumesi ve bir b sayisi b nin toplamlarindan olusan A nin bir altkumesi Bununla birlikte eger sayi kumesi ise soyle ki sayi kumesinin her bir elemani onceki sayilarin tamaminin toplamindan daha buyuk olmali problem ile beklenen zamanda ve kolayca cozulebilir Anahtar uretimi Merkle Hellman algoritmasinda anahtarlar birer sirt cantalaridir Acik anahtar A nin kolayca kirilamayan sirt cantasidir ve Gizli Anahtar da B nin basit ya da super artan bir sirt cantasi bir carpan ve bir modulden olusan iki ek sayinin birlesimidir Carpan ve modul super artan sirt cantasindan kolay kirilamayan sirt cantasina cevirmede kullanilabilir Eger problem beklenen zamanda cozulebilirse Ayni sayilar kolay kirilamayan sirt cantasinin altkume toplaminin basit sirt cantasinin altkume toplamina cevrilmesinde kullanilabilir Sifreleme Mesaji sifrelemek icin A nin kolay kirilamayan sirt cantasinin altkumesinden secilen anahtar uzunlugunda bit kumesi ile karsilastirilir Acik anahtardaki her bir terim duz metindeki bir elemani A m altkumesinin bir elemanini karsilar duz metindeki 0 A m kumesinin insa edilmesini goz ardi eder Bu altkumenin elemanlari toplanmis ve toplamanin sonucu sifrelenmis metindir Desifreleme Desifreleme mumkundur cunku carpan ve modul kolayca cevrilebilir super artan sirt cantasindaki acik anahtar boylece super artan sirt cantasindaki elemanlarin karsilandigi toplamdaki sifreli metin sayi donusturme cevriminde kullanilabilir Sonra basit bir Greedy Algoritmasi kullanilarak basit sirt cantasi Buyuk o gosterimindeki aritmetik operatorler kullanilarak cozulur Boylece mesaj desifrelenmis olur Matematiksel metotAnahtar uretimi n bitten olusan mesaji sifrelemek icin superartan bir dizi secilir w w1 w2 wn n sifirdan farkli dogal sayi q gibi bir rastgele sayi secilir q gt i 1nwi displaystyle q gt sum i 1 n w i ve r gibi rastgele bir sayi secilir Ortak bolen r q 1 r ve q Aralarinda asal q nun boyle secilmesi sifrelenmis metnin benzersiz olmasini saglar Eger q duz metinden daha kucuk secilirse ayni sifrelenmis metinler elde edilebilir r ile q aralarinda asal olmalidir yoksa mod q gore tersine cevrilemeyecektir q nun tersinin olmasi gereklidir Boylece desifreleme yapilabilir Simdi diziyi hesaplayalim b b1 b2 bn bi rwi mod q Acik Anahtar b ve Gizli Anahtarlar w q r dir Sifreleme n bit mesaji sifrelemek icin a a1 a2 an ai displaystyle alpha i mesajin i biti ve ai displaystyle alpha i boldsymbol in 0 1 c i 1naibi displaystyle c sum i 1 n alpha i beta i Sifrelenmis metin c dir Desifreleme Desifreleme amaciyla alinan bir c sifreli mesaji ai displaystyle alpha i gibi bir biti ile su sekilde uyusur c i 1naibi displaystyle c sum i 1 n alpha i beta i bi rastgele degerler aldigindan dolayi bu zor bir problem olabilir Cunku alici alt kume probleminin ornek bir cozumune sahip olmalidir Anahtar Sifreleme s tam sayilarini r mod q nun moduler tersinden bulmaktir Bunun anlami s r mod q 1 den s yi ya da s r k q 1 k gibi bir tam sayi bulmaktir r Ortak bolen r q 1 den secildiginden kullanilarak k ve s bulunabilir Alici c sifreli metnini hesaplar c cs modq displaystyle c equiv cs pmod q Bu yuzden c cs i 1naibis modq displaystyle c equiv cs equiv sum i 1 n alpha i beta i s pmod q Cunku rs mod q 1 ve bi rwi mod q bis wirs wi modq displaystyle beta i s equiv w i rs equiv w i pmod q Bu yuzden c i 1naiwi modq displaystyle c equiv sum i 1 n alpha i w i pmod q Butun wi degerlerinin toplami q dan kucuktur ve bu yuzden i 1naiwi displaystyle sum i 1 n alpha i w i 0 q 1 araligindadir Boylece alici alt kume problemini cozmus olur c i 1naiwi displaystyle c sum i 1 n alpha i w i Ornek Ilk olarak super artan bir dizi olan w yi olusturalim w 2 7 11 21 42 89 180 354 Bu Gizli Anahtar icin temeldir Buradan toplami hesaplayalim w 706 displaystyle sum w 706 Sonra toplamdan buyuk bir q sayisi secelim q 881 Ayrica 1 q displaystyle 1 q araliginda q ile Aralarinda asal bir r sayisi secelim r 588 q w ve r den olusan Gizli anahtarimiz olusmus oldu w kumesinin her bir elemanini rmodq ile carparak b kumesini uretiyoruz b 295 592 301 14 28 353 120 236 Cunku2 588 mod 881 295 7 588 mod 881 592 11 588 mod 881 301 21 588 mod 881 14 42 588 mod 881 28 89 588 mod 881 353 180 588 mod 881 120 354 588 mod 881 236 b kumesi ile Acik Anahtarimizi olusturmus olduk Ayse a yi sifrelemek istedigini soylesin Ilk once Ayse a nin ikili tabandaki degerini bulmalidir bu durumda ASCII ya da UTF 8 kullanilmalidir 01100001 Ayse sirasiyla her bir biti b kumesindeki eslesen her bir elemanla carpmalidir a 01100001 0 295 1 592 1 301 0 14 0 28 0 353 0 120 1 236 1129 Bunu aliciya gondermelidir Ali desifrelerken bu sayiyi r 1 mod q displaystyle q ile carpmalidir 1129 442 mod 881 372 Simdi Ali 372 den w kumesinden secilen 372 ye esit ya da 372 den kucuk en buyuk sayiyi cikararak en son fark 0 displaystyle 0 oluncaya kadar isleme devam edilir 372 354 18 18 11 7 7 7 0 Sectigimiz elemanlarin yerine 1 yazdigimizda ortaya gonderilen mesajin ikili karsiligi cikmis olur 01100001 Bu ikili kod geri cevrildiginde Ayse nin Ali ye yolladigi a mesajina ulasmis oluruz Kaynakca Merkle Ralph Hellman Martin 1978 Hiding information and signatures in trapdoor knapsacks IEEE Transactions on Information Theory 24 5 ss 525 530 doi 10 1109 TIT 1978 1055927 Shamir Adi 1984 A polynomial time algorithm for breaking the basic Merkle Hellman cryptosystem IEEE Transactions on Information Theory 30 5 ss 699 704 doi 10 1109 SFCS 1982 5
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans