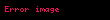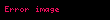Merkle imzası, anahtarlama ağaçları ve sayısal imza şemalarını birleştiren bir veri doğrulama yapısıdır. Özet değeri tabanlı kriptografidir ve Merkle ağacı da denen özet değeri ağacını kullanmaktadır. Verileri gibi tek kullanımlık şekilde imzalar. tarafından 1970 sonu itibarıyla geliştirilmiştir ve RSA, Dijital İmza Algoritması gibi geleneksel dijital imzalara alternatif olmuştur.
Merkle imza algoritmasının avantajı kuantum bilgisayarı algoritmalarına karşı dirençli olduğuna inanılıyor olmasıdır. Geleneksel açık anahtar algoritmaları olan RSA ve ElGamal gibi algoritmalar efektif kuantum bilgisayarlarının tasarlanabilir olmasıyla birlikte (Shor'un algoritmasına dayanarak) güvensiz hale geldi. Merkle imza algoritması sadece güvenilir bir özet değeri fonksiyonunun varlığına dayanmaktadır. Bu özelliği de Merkle imza algoritmasının çok esnek ve kuantum bilgisayarlarına dirençli olmasını sağlamaktadır. Merkle imzasının sonlu imza potansiyeli olan tek kullanımlık bir imza olduğu unutulmamalıdır; ve 'un imza tabanlı tek yölü permütasyonlar üzerindeki çalışması ve fonksiyonlar (ve icadı), Merkle benzeri imzaların tam bir imza algoritmasına dönüşmesine yol açmıştır.
Anahtar Oluşturma
Merkle imza algoritması tek açık anahtar olan pub ile sınırlı sayıda mesajın imzasında kullanılabilir. Muhtemel mesajların sayısı ikinin katı olmalıdır, dolayısıyla olası mesajların sayısını N = 2n ile gösterelim.
Ortak anahtar olan pub oluşturulması için ilk aşama N tane tek kullanımlık imza algoritmalarının (Lamport imza algoritması gibi) özel/açık anahtar çifti (Xi,Yi) üretilmelidir. Her 1<= I <= 2n için, ortak anahtarın özet değeri hi = H(Yi) hesaplanır.

Bütün 
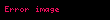

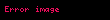


Merkle imza algoritmasının özel anahtarı bütün (Xi,Yi) çiftleridir. Algoritmanın en büyük problemlerinden birisi bu özel anahtar kümesinin boyutunun mesaj sayısıyla doğrusal oranda büyüyor olmasıdır.
Açık anahtar pub ağacın kökü olan =an,0 değeridir. Tek açık anahtar Yi 'nin genele açılması güvenliği kırmayacaktır. Ancak, bunların kullanımı genel için bir ihtiyaç değildir ve boyutlarını da küçültmek adına gizli tutmak mantıklı olacaktır.
İmza Oluşturma
Merkle imza algoritması ile M mesajını imzalamak için imzalayan bir (Xi,Yi) anahtar çifti seçer, tek kullanımlık imza algoritması kullanarak imzalar ve ardından ek bilgileri ekleyerek aslında onun orijinal anahtar çiftlerinden biri olduğunu kanıtlar (bir sahtekar tarafından yeni yaratılanın yerine).
İlk olarak, imzalayıcı daha önce başka bir mesajı imzalamak için kullanılmamış (Xi,Yi) çifti seçer ve tek kullanımlık imza algoritmasını mesajı imzalamak için kullanarak sig' imzasını ve karşılık gelen Yi açık anahtarını elde eder. Mesaj alıcısına (Xi,Yi) çiftinin orijinal anahtar çiftlerinden biri olduğunu kanıtlamak için Merkle ağacının ara düğümlerini dahil ederek alıcının hi=a0,i değerinin ağacın kökünde bulunan an,o açık anahtarını hesaplamak için kullanıldığını doğrulamasını sağlar . a0,i değerinden kök değerine giden yolda n+1 düğüm bulunur ve bunların her birini A0,...., An şeklinde ifade ederiz. A0 = a0,i = H(Yi) yaprak değeri ve An = an,0 = pub ise kök değeri olmuş olur.





Bu düğümler auth0,…,authn-1, Yi ve tek kullanımlık imza olan sig’ birlikte Merkle imza algoritması kullanarak bir M imzası oluştururlar:
sig = (sig’ || Yi || auth0|| auth1 ||…|| authn-1)
Ayrıca unutulmamalıdır ki Lamport imza algoritması imza için kullanılırken, sig’ özel anahtar Xi'nin bir bölümünü içerir.
İmza doğrulaması
Alıcı açık anahtar pub, mesaj M ve imza sig = (sig’ || Yi || auth0|| auth1 ||…|| authn-1) bilmektedir.İlk olarak alıcı tek kullanımlık imza açık anahtarı Yi kullanarak mesaja ait olan tek kullanımlık imza sig’ doğrular. Eğer sig’ M mesajına ait geçerli bir imza ise, alıcı tek kullanımlık imzanın açık anahtarının özet değerini alarak A0 = H(Yi) hesaplar. j = 1,…, n-1 değerleri için, yol üzerindeki Aj düğümleri Aj = H(Aj-1 || authj-1) ile hesaplanır. Eğer An Merkle anahtar algoritmasına ait açık anahtar pub’a eşit ise imza geçerlidir.
Kaynakça
- G. Becker. "Merkle Signature Schemes, Merkle Trees and Their Cryptanalysis", seminar 'Post Quantum Cryptology' at the Ruhr-University Bochum, Germany.
- E. Dahmen, M. Dring, E. Klintsevich, J. Buchmann, L.C. Coronado Garca. "CMSS - an improved merkle signature scheme". Progress in Cryptology - Indocrypt 2006, 2006.
- E. Klintsevich, K. Okeya, C.Vuillaume, J. Buchmann, E.Dahmen. "Merkle signatures with virtually unlimited signature capacity". 5th International Conference on Applied Cryptography and Network Security - ACNS07, 2007.
- Ralph Merkle. "Secrecy, authentication and public key systems / A certified digital signature". Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University, 1979. [1] 14 Ağustos 2018 tarihinde Wayback Machine sitesinde .
- Moni Naor, Moti Yung: Universal One-Way Hash Functions and their Cryptographic Applications .STOC 1989: 33-43
- S. Micali, M. Jakobsson, T. Leighton, M. Szydlo. "Fractal merkle tree representation and traversal". RSA-CT 03, 2003
Dış bağlantılar
- Efficient Use of Merkle Trees 17 Nisan 2017 tarihinde Wayback Machine sitesinde . -Merkle ağaçlarının asıl amacı olan birden fazla tek kullanımlık Lambort imzasının ele alınmasının RSA Labs tarafından açıklanması
- An introduction to hash-based signatures and Merkle signatures by Adam Langley. 14 Eylül 2018 tarihinde Wayback Machine sitesinde .
- A 4 parts series on hash-based signatures by David Wong. 5 Şubat 2018 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Merkle imzasi anahtarlama agaclari ve sayisal imza semalarini birlestiren bir veri dogrulama yapisidir Ozet degeri tabanli kriptografidir ve Merkle agaci da denen ozet degeri agacini kullanmaktadir Verileri gibi tek kullanimlik sekilde imzalar tarafindan 1970 sonu itibariyla gelistirilmistir ve RSA Dijital Imza Algoritmasi gibi geleneksel dijital imzalara alternatif olmustur Merkle imza algoritmasinin avantaji kuantum bilgisayari algoritmalarina karsi direncli olduguna inaniliyor olmasidir Geleneksel acik anahtar algoritmalari olan RSA ve ElGamal gibi algoritmalar efektif kuantum bilgisayarlarinin tasarlanabilir olmasiyla birlikte Shor un algoritmasina dayanarak guvensiz hale geldi Merkle imza algoritmasi sadece guvenilir bir ozet degeri fonksiyonunun varligina dayanmaktadir Bu ozelligi de Merkle imza algoritmasinin cok esnek ve kuantum bilgisayarlarina direncli olmasini saglamaktadir Merkle imzasinin sonlu imza potansiyeli olan tek kullanimlik bir imza oldugu unutulmamalidir ve un imza tabanli tek yolu permutasyonlar uzerindeki calismasi ve fonksiyonlar ve icadi Merkle benzeri imzalarin tam bir imza algoritmasina donusmesine yol acmistir Anahtar OlusturmaMerkle imza algoritmasi tek acik anahtar olan pub ile sinirli sayida mesajin imzasinda kullanilabilir Muhtemel mesajlarin sayisi ikinin kati olmalidir dolayisiyla olasi mesajlarin sayisini N 2n ile gosterelim Ortak anahtar olan pub olusturulmasi icin ilk asama N tane tek kullanimlik imza algoritmalarinin Lamport imza algoritmasi gibi ozel acik anahtar cifti Xi Yi uretilmelidir Her 1 lt I lt 2n icin ortak anahtarin ozet degeri hi H Yi hesaplanir 8 yaprakli Merkle Agaci Butun hi displaystyle h i 2n displaystyle 2 n yaprak ozet degeri ozyineli bir sekilde ozet degerleri alinarak ikili agac formasyonunda Merkle agaci olusturulur ai j displaystyle a i j ifadesinde yukseklik icin i displaystyle i ve sag sol pozisyonu gostermek icinse j displaystyle j Buna istinaden hi a0 i displaystyle h i a 0 i ozet degerleri yapraklari temsil etmektedir Her ic dugumlerin degeri kendi alt 2 cocugunun degerlerinin birlesiminin ozet degerlerinin alinmasi ile belirlenir Ornegin a1 0 H a0 0 a0 1 displaystyle a 1 0 H a 0 0 a 0 1 ve a2 0 H a1 0 a1 1 displaystyle a 2 0 H a 1 0 a 1 1 Bu sekilde 2n displaystyle 2 n yaprakli bir agacta 2n 1 1 displaystyle 2 n 1 1 dugum olusturulmaktadir Merkle imza algoritmasinin ozel anahtari butun Xi Yi ciftleridir Algoritmanin en buyuk problemlerinden birisi bu ozel anahtar kumesinin boyutunun mesaj sayisiyla dogrusal oranda buyuyor olmasidir Acik anahtar pub agacin koku olan an 0 degeridir Tek acik anahtar Yi nin genele acilmasi guvenligi kirmayacaktir Ancak bunlarin kullanimi genel icin bir ihtiyac degildir ve boyutlarini da kucultmek adina gizli tutmak mantikli olacaktir Imza OlusturmaMerkle imza algoritmasi ile M mesajini imzalamak icin imzalayan bir Xi Yi anahtar cifti secer tek kullanimlik imza algoritmasi kullanarak imzalar ve ardindan ek bilgileri ekleyerek aslinda onun orijinal anahtar ciftlerinden biri oldugunu kanitlar bir sahtekar tarafindan yeni yaratilanin yerine Ilk olarak imzalayici daha once baska bir mesaji imzalamak icin kullanilmamis Xi Yi cifti secer ve tek kullanimlik imza algoritmasini mesaji imzalamak icin kullanarak sig imzasini ve karsilik gelen Yi acik anahtarini elde eder Mesaj alicisina Xi Yi ciftinin orijinal anahtar ciftlerinden biri oldugunu kanitlamak icin Merkle agacinin ara dugumlerini dahil ederek alicinin hi a0 i degerinin agacin kokunde bulunan an o acik anahtarini hesaplamak icin kullanildigini dogrulamasini saglar a0 i degerinden kok degerine giden yolda n 1 dugum bulunur ve bunlarin her birini A0 An seklinde ifade ederiz A0 a0 i H Yi yaprak degeri ve An an 0 pub ise kok degeri olmus olur Merkle agacinda i 2 icin A ve kimlik dogrulama yolu Ai displaystyle A i dugumunun Ai 1 displaystyle A i 1 Alicinin onceki verilmis olanla bir sonraki dugum Ai 1 displaystyle A i 1 Ai 1 displaystyle A i 1 Bu dugume authi displaystyle text auth i boylece Ai 1 H Ai authi displaystyle A i 1 H A i text auth i Bu sebeple auth0 authn 1 displaystyle text auth 0 ldots text auth n 1 An an 0 pub displaystyle A n a n 0 text pub A0 a0 i displaystyle A 0 a 0 i bir kimlik dogrulama yolu sag taraftaki sekilde gosterilmektedir Bu dugumler auth0 authn 1 Yi ve tek kullanimlik imza olan sig birlikte Merkle imza algoritmasi kullanarak bir M imzasi olustururlar sig sig Yi auth0 auth1 authn 1 Ayrica unutulmamalidir ki Lamport imza algoritmasi imza icin kullanilirken sig ozel anahtar Xi nin bir bolumunu icerir Imza dogrulamasiAlici acik anahtar pub mesaj M ve imza sig sig Yi auth0 auth1 authn 1 bilmektedir Ilk olarak alici tek kullanimlik imza acik anahtari Yi kullanarak mesaja ait olan tek kullanimlik imza sig dogrular Eger sig M mesajina ait gecerli bir imza ise alici tek kullanimlik imzanin acik anahtarinin ozet degerini alarak A0 H Yi hesaplar j 1 n 1 degerleri icin yol uzerindeki Aj dugumleri Aj H Aj 1 authj 1 ile hesaplanir Eger An Merkle anahtar algoritmasina ait acik anahtar pub a esit ise imza gecerlidir KaynakcaG Becker Merkle Signature Schemes Merkle Trees and Their Cryptanalysis seminar Post Quantum Cryptology at the Ruhr University Bochum Germany E Dahmen M Dring E Klintsevich J Buchmann L C Coronado Garca CMSS an improved merkle signature scheme Progress in Cryptology Indocrypt 2006 2006 E Klintsevich K Okeya C Vuillaume J Buchmann E Dahmen Merkle signatures with virtually unlimited signature capacity 5th International Conference on Applied Cryptography and Network Security ACNS07 2007 Ralph Merkle Secrecy authentication and public key systems A certified digital signature Ph D dissertation Dept of Electrical Engineering Stanford University 1979 1 14 Agustos 2018 tarihinde Wayback Machine sitesinde Moni Naor Moti Yung Universal One Way Hash Functions and their Cryptographic Applications STOC 1989 33 43 S Micali M Jakobsson T Leighton M Szydlo Fractal merkle tree representation and traversal RSA CT 03 2003Dis baglantilarEfficient Use of Merkle Trees 17 Nisan 2017 tarihinde Wayback Machine sitesinde Merkle agaclarinin asil amaci olan birden fazla tek kullanimlik Lambort imzasinin ele alinmasinin RSA Labs tarafindan aciklanmasi An introduction to hash based signatures and Merkle signatures by Adam Langley 14 Eylul 2018 tarihinde Wayback Machine sitesinde A 4 parts series on hash based signatures by David Wong 5 Subat 2018 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans