Mie saçılması veya Mie teorisi, düzlem bir elektromanyetik dalganın (ışık) homojen bir küre tarafından saçılmasını ifade eder. Maxwell denklemlerinin Lorenz–Mie–Debye çözümü olarak da bilinmektedir. Denklemlerin çözümü sonsuz bir serisi şeklinde yazılır. Saçılma ismini fizikçi Gustav Mie'den almaktadır; analitik çözümü ilk kez 1908 yılında yayınlanmıştır.

"Mie saçılması" terimi aynı zamanda ışığın dalga boyunun kürenin yarıçapı ile yaklaşık eşit olduğu saçılma durumları için de kullanılmaktadır; bu saçılma özellikle atmosferde görülür. Genel Mie saçılmasının teknik olarak bir boyut limiti yoktur: saçılma sonuçları kürenin dalga boyundan küçük olduğunu durumlarda Rayleigh saçılmasına, büyük olduğu özel durumlarda ise geometrik optiğe yakınsar. Mie saçılması ve tesir kesitinin hesaplanması için birçok kod bulunmaktadır; Mie teorisinin konsentrik küreler, sonsuz silindir ve küre kümelerine uygulandığı kodlar da mevcuttur.
Teori

Mie saçılmasında çarpan ve saçılan elektrik alanlar olarak yazılır. Helmholtz denkleminin küresel koordinat sisteminde değişkenlerin ayrımı ile çözülmesi ile elde edilir. Kürenin yüzeyinde elektromanyetik sınır koşulları sağlanarak saçılan dalga farklı katsayılarda (çok kutuplu) harmonikler cinsinden gösterilir. Işık saçılma oranı genellikle optik tesir kesiti ile ifade edilir ve bu katsayı Mie saçılması ile elde edilebilir. Teori kullanarak Mie rezonansları ve saçılma katsayıları da bulunabilmektedir.
Işığın dalga boyunun kürenin yarıçapına oranına ve malzeme özelliklerine göre farklı yaklaşım ve tanımlamalarda bulunulabilir. Rayleigh saçılması dalga boyundan çok daha küçük parçacıklardaki ışık saçılmasını belirtir. Bu dalga boyları için yarı-statik yaklaşım kullanılarak Laplace denklemi de çözülebilir. Rayleigh–Gans yaklaşımı ve ayrıksı kırınım teorisi (van de Hulst yaklaşımı) parçacığın kırılma indisinin bulunduğu ortamınkine çok yakın olduğu durumlarda kullanılabilir. Yaklaşımlar her ne kadar birçok uygulamada iş görse de atmosferdeki su damlacıklarındaki, hücrelerdeki ve emülsiyonlardaki saçılmaların hesaplanması için tam teorinin kullanılması esastır.
Matematiksel temeller
Mie saçılmasının türetilmesi

Mie saçılmasının standart analitik çözümü genelde z-ekseninde hareket eden ve x-ekseninde polarize olmuş bir düzlem dalga için yapılır. Parçacığın yalıtkanlık sabiti ve manyetik geçirgenliği 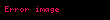



Saçılma probleminin çözümü için öncelikle vektör Helmholtz denklemi küresel koordinatlarda yazılır. Helmholtz denklemi, elektrik ve manyetik alanlar için şu şekilde gösterilir:
Helmholtz denklemi dışında, alanların 





Küresel koordinatlarda açılan dalga denklemi şu şekilde ifade edilebilir:
Bu denklem değişkenlerin ayrımı yöntemi ile çözülür. Denklemin çözümüne göre üreten fonksiyonunu sağlayan vektör küresel harmonikler şu şekilde ifade edilir:
— manyetik harmonikler (TE)
— elektrik harmonikler (TM)
ve


Daha sonrasında küreye çarpan düzlem dalga vektör küresel harmonikler cinsinden açılır:
Buradaki 


Sonrasında şu koşullar çözümde göz önünde bulundurulur:
- Kürenin yüzeyinde elektromanyetik sınır koşulları sağlanmalıdır.
- Saçılma probleminin çözümü orijinde sınırlandırılmalıdır: bu nedenle kürenin içindeki alanların üreten fonksiyonu olarak küresel Bessel fonksiyonları seçilir.
- Saçılan alan, orijinden sonsuza doğru hareket etmelidir; bunun için birinci tip Hankel fonksiyonları seçilir.
Saçılan alanlar, daha sonra vektör harmonik açılımla şu şekilde yazılır:
Bu denklemlerde 

Kürenin içindeki alanlar ise şu şekilde açılabilir:




Sınır koşulları denklemlere uygulandıktan sonra Mie katsayıları elde edilir:
Bu katsayılarda 


Mie saçılması nümerik olarak hesaplanırken sonsuz seri toplamının bir yerden sonra kesilmesi gerekir. Bununla ilgili en yaygın kriterlerden biri Wiscombe'un kriteridir ve 

Saçılma ve yok olma tesir kesitleri

Mie teorisinde ve saçılmada etkinlik katsayıları sıklıkla kullanılan parametrelerdendir. Bu katsayılar yok olma 



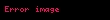
Yok olma kesiti, Mie teorisinde şu şekilde tanımlanır:
and
Gene Mie teorisine göre, saçılma ve yok olma katsayıları sonsuz bir seri ile gösterilebilir:
Uygulamalar

Mie teorisi, atmosfer biliminde bulut ve tozlardaki ışık saçılmasının incelenmesi için sıkça kullanılmaktadır. Teorinin diğer kullanım alanları arasında biyomedikal sistemler ile radarlar bulunmaktadır. Mie saçılımı aynı zamanda bazı metamateryal ve plazmonik yapıların teorisinde yer edinmiştir.
Kaynakça
- ^ a b c d e Bohren & Huffman 2010, s. 82-97.
- ^ Jackson 1998, s. 473-478.
- ^ van de Hulst 1957.
- ^ a b Maier 2007.
- ^ a b Bohren & Huffman 2010, s. 82-129.
- ^ Wiscombe, W. J. (1980). "Improved Mie scattering algorithms". Applied Optics. 19 (9): 1505-1509. doi:10.1364/AO.19.001505.
- ^ Survikov ST (2011). "Mie Scattering". A-to-Z Guide to Thermodynamics, Heat and Mass Transfer, and Fluids Engineering. Thermopedia. doi:10.1615/AtoZ.m.mie_scattering. ISBN . Erişim tarihi: 28 Ocak 2019.
- ^ Ye Z, Jiang X, Wang Z (Oct 2012). (PDF). Journal of Software. 7 (10): 2309-2316. 28 Ocak 2019 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 15 Haziran 2020.
- ^ Zhao, Q.; Zhou, J.; Zhang, F. L.; Lippens, D. (2009). "Mie resonance-based dielectric metamaterials". Materials Today. 12 (12): 60-69. doi:10.1016/S1369-7021(09)70318-9.
- ^ Halas, Naomi J.; Lal, Surbhi; Chang, Wei-Shun; Link, Stephan; Nordlander, Peter (2011). "Plasmons in strongly coupled metallic nanostructures". Chemical Reviews. 111 (6): 3913-3961. doi:10.1021/cr200061k.
Kitap kaynakları
- Bohren, C. F.; Huffmann, D. R. (2010). Absorption and scattering of light by small particles (İngilizce). New York: Wiley-Interscience. ISBN .
- Jackson, John David (1998). Classical Electrodynamics (İngilizce). New York: Wiley. ISBN .
- Maier, S. A. (2007). Plasmonics: Fundamentals and applications (İngilizce). New York: Springer. ISBN .
- van de Hulst, H. C. (1957). Light scattering by small particles (İngilizce). New York: John Wiley and Sons. ISBN .
Dış bağlantılar
- SCATTERLIB: Işık saçılması kodları koleksiyonu 26 Kasım 2020 tarihinde Wayback Machine sitesinde .
- Online Mie saçılması hesaplayıcısı 29 Ocak 2020 tarihinde Wayback Machine sitesinde .
- PyMieScatt 21 Ekim 2020 tarihinde Wayback Machine sitesinde ., Mie saçılması Python kodu
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Mie sacilmasi veya Mie teorisi duzlem bir elektromanyetik dalganin isik homojen bir kure tarafindan sacilmasini ifade eder Maxwell denklemlerinin Lorenz Mie Debye cozumu olarak da bilinmektedir Denklemlerin cozumu sonsuz bir serisi seklinde yazilir Sacilma ismini fizikci Gustav Mie den almaktadir analitik cozumu ilk kez 1908 yilinda yayinlanmistir Mie sacilmasinin semasi Mie sacilmasi terimi ayni zamanda isigin dalga boyunun kurenin yaricapi ile yaklasik esit oldugu sacilma durumlari icin de kullanilmaktadir bu sacilma ozellikle atmosferde gorulur Genel Mie sacilmasinin teknik olarak bir boyut limiti yoktur sacilma sonuclari kurenin dalga boyundan kucuk oldugunu durumlarda Rayleigh sacilmasina buyuk oldugu ozel durumlarda ise geometrik optige yakinsar Mie sacilmasi ve tesir kesitinin hesaplanmasi icin bircok kod bulunmaktadir Mie teorisinin konsentrik kureler sonsuz silindir ve kure kumelerine uygulandigi kodlar da mevcuttur TeoriElektrik ve manyetik vektor kuresel harmoniklerinin acisal kisimlari Kirmizi ve yesil oklar alanin yonunu gostermektedir Mie sacilmasinda carpan ve sacilan elektrik alanlar olarak yazilir Helmholtz denkleminin kuresel koordinat sisteminde degiskenlerin ayrimi ile cozulmesi ile elde edilir Kurenin yuzeyinde elektromanyetik sinir kosullari saglanarak sacilan dalga farkli katsayilarda cok kutuplu harmonikler cinsinden gosterilir Isik sacilma orani genellikle optik tesir kesiti ile ifade edilir ve bu katsayi Mie sacilmasi ile elde edilebilir Teori kullanarak Mie rezonanslari ve sacilma katsayilari da bulunabilmektedir Isigin dalga boyunun kurenin yaricapina oranina ve malzeme ozelliklerine gore farkli yaklasim ve tanimlamalarda bulunulabilir Rayleigh sacilmasi dalga boyundan cok daha kucuk parcaciklardaki isik sacilmasini belirtir Bu dalga boylari icin yari statik yaklasim kullanilarak Laplace denklemi de cozulebilir Rayleigh Gans yaklasimi ve ayriksi kirinim teorisi van de Hulst yaklasimi parcacigin kirilma indisinin bulundugu ortaminkine cok yakin oldugu durumlarda kullanilabilir Yaklasimlar her ne kadar bircok uygulamada is gorse de atmosferdeki su damlaciklarindaki hucrelerdeki ve emulsiyonlardaki sacilmalarin hesaplanmasi icin tam teorinin kullanilmasi esastir Matematiksel temellerMie sacilmasinin turetilmesi z ekseninde hareket eden ve x ekseninde polarize olmus bir duzlem dalganin sacilmasi Kurenun yaricapi a dir Mie sacilmasinin standart analitik cozumu genelde z ekseninde hareket eden ve x ekseninde polarize olmus bir duzlem dalga icin yapilir Parcacigin yalitkanlik sabiti ve manyetik gecirgenligi e1 displaystyle varepsilon 1 ve m1 displaystyle mu 1 ile gosterilirken parcacigin bulundugu ortamdaki degerler e displaystyle varepsilon ve m displaystyle mu ile gosterilir Sacilma probleminin cozumu icin oncelikle vektor Helmholtz denklemi kuresel koordinatlarda yazilir Helmholtz denklemi elektrik ve manyetik alanlar icin su sekilde gosterilir 2E k2E 0 2H k2H 0 displaystyle nabla 2 mathbf E k 2 mathbf E 0 nabla 2 mathbf H k 2 mathbf H 0 Helmholtz denklemi disinda alanlarin E H 0 displaystyle nabla cdot mathbf E nabla cdot mathbf H 0 E iwmH displaystyle nabla times mathbf E i omega mu mathbf H ve H iweE displaystyle nabla times mathbf H i omega varepsilon mathbf E kosullarini saglamasi gerekir Daha sonra M displaystyle mathbf M ve N displaystyle mathbf N kuresel harmoniklerinin ureten fonksiyonu olarak kabul edebilecegimiz skalar ps displaystyle psi fonksiyonu denkleme eklenir vektor kuresel harmonikler gerekli kosullari saglamaktadir Kuresel koordinatlarda acilan dalga denklemi su sekilde ifade edilebilir 1r2 r r2 ps r 1r2sin8 8 sin8 ps 8 1r2sin8 2ps ϕ2 k2ps 0 displaystyle frac 1 r 2 frac partial partial r left r 2 frac partial psi partial r right frac 1 r 2 sin theta frac partial partial theta left sin theta frac partial psi partial theta right frac 1 r 2 sin theta left frac partial 2 psi partial phi 2 right k 2 psi 0 Bu denklem degiskenlerin ayrimi yontemi ile cozulur Denklemin cozumune gore ureten fonksiyonunu saglayan vektor kuresel harmonikler su sekilde ifade edilir Moemn rpsoemn displaystyle mathbf M e o mn nabla times left mathbf r psi e o mn right manyetik harmonikler TE Noemn Moemnk displaystyle mathbf N e o mn frac nabla times mathbf M e o mn mathbf k elektrik harmonikler TM ve psemn cos mfPnm cos ϑ zn kr displaystyle psi emn cos m varphi P n m cos vartheta z n k r psomn sin mfPnm cos ϑ zn kr displaystyle psi omn sin m varphi P n m cos vartheta z n k r Pnm cos 8 displaystyle P n m cos theta ve zn kr displaystyle z n k r ise kuresel Bessel fonksiyonlarini gosterir Daha sonrasinda kureye carpan duzlem dalga vektor kuresel harmonikler cinsinden acilir Einc E0eikrcos 8ex E0 n 1 in2n 1n n 1 Mo1n 1 k r iNe1n 1 k r displaystyle mathbf E inc E 0 e ikr cos theta mathbf e x E 0 sum n 1 infty i n frac 2n 1 n n 1 left mathbf M o1n 1 k mathbf r i mathbf N e1n 1 k mathbf r right Hinc kwmE0 n 1 in2n 1n n 1 Me1n 1 k r iNo1n 1 k r displaystyle mathbf H inc frac k omega mu E 0 sum n 1 infty i n frac 2n 1 n n 1 left mathbf M e1n 1 k mathbf r i mathbf N o1n 1 k mathbf r right Buradaki 1 displaystyle 1 ust imi psoemn displaystyle psi e o mn fonksiyonun radyal kisminin kuresel Bessel fonksiyonu oldugunu belirtir Acilim katsayilari ise su integraller ile elde edilir 02p 0pEinc Moemn 1 sin 8d8df 02p 0p Moemn 1 2sin 8d8df displaystyle frac int 0 2 pi int 0 pi mathbf E inc cdot mathbf M e o mn 1 sin theta d theta d varphi int 0 2 pi int 0 pi mathbf M e o mn 1 2 sin theta d theta d varphi m 1 displaystyle m neq 1 i saglayan tum katsayilar 0 dir Sonrasinda su kosullar cozumde goz onunde bulundurulur Kurenin yuzeyinde elektromanyetik sinir kosullari saglanmalidir Sacilma probleminin cozumu orijinde sinirlandirilmalidir bu nedenle kurenin icindeki alanlarin ureten fonksiyonu olarak kuresel Bessel fonksiyonlari secilir Sacilan alan orijinden sonsuza dogru hareket etmelidir bunun icin birinci tip Hankel fonksiyonlari secilir Sacilan alanlar daha sonra vektor harmonik acilimla su sekilde yazilir Es n 1 En ianNe1n 3 k r bnMo1n 3 k r displaystyle mathbf E s sum n 1 infty E n left ia n mathbf N e1n 3 k mathbf r b n mathbf M o1n 3 k mathbf r right Hs kwm n 1 En anMe1n 3 k r ibnNo1n 3 k r displaystyle mathbf H s frac k omega mu sum n 1 infty E n left a n mathbf M e1n 3 k mathbf r ib n mathbf N o1n 3 k mathbf r right Bu denklemlerde 3 displaystyle 3 ust imi psoemn displaystyle psi e o mn fonksiyonun radyal kisminin kuresel Hankel fonksiyonu oldugunu belirtir Kurenin icindeki alanlar ise su sekilde acilabilir E1 n 1 En idnNe1n 1 k1 r cnMo1n 1 k1 r displaystyle mathbf E 1 sum n 1 infty E n left id n mathbf N e1n 1 k 1 mathbf r c n mathbf M o1n 1 k 1 mathbf r right H1 k1wm1 n 1 En dnMe1n 1 k1 r icnNo1n 1 k1 r displaystyle mathbf H 1 frac k 1 omega mu 1 sum n 1 infty E n left d n mathbf M e1n 1 k 1 mathbf r ic n mathbf N o1n 1 k 1 mathbf r right k wcn displaystyle k frac omega c n ve k1 wcn1 displaystyle k 1 frac omega c n 1 kure disindaki ve icindeki dalga vektorunu ifade eder Kurenin disi ve icindeki kirilma indisleri n displaystyle n ve n1 displaystyle n 1 ile gosterilir Sinir kosullari denklemlere uygulandiktan sonra Mie katsayilari elde edilir cn w m1 rhn r jn r m1 rjn r hn r m1 rhn r jn r1 m r1jn r1 hn r displaystyle c n omega frac mu 1 left rho h n rho right j n rho mu 1 left rho j n rho right h n rho mu 1 left rho h n rho right j n rho 1 mu left rho 1 j n rho 1 right h n rho dn w m1n1n rhn r jn r m1n1n rjn r hn r mn12 rhn r jn r1 m1n2 r1jn r1 hn r displaystyle d n omega frac mu 1 n 1 n left rho h n rho right j n rho mu 1 n 1 n left rho j n rho right h n rho mu n 1 2 left rho h n rho right j n rho 1 mu 1 n 2 left rho 1 j n rho 1 right h n rho bn w m1 rjn r jn r1 m r1jn r1 jn r m1 rhn r jn r1 m r1jn r1 hn r displaystyle b n omega frac mu 1 left rho j n rho right j n rho 1 mu left rho 1 j n rho 1 right j n rho mu 1 left rho h n rho right j n rho 1 mu left rho 1 j n rho 1 right h n rho an w mn12 rjn r jn r1 m1n2 r1jn r1 jn r mn12 rhn r jn r1 m1n2 r1jn r1 hn r displaystyle a n omega frac mu n 1 2 left rho j n rho right j n rho 1 mu 1 n 2 left rho 1 j n rho 1 right j n rho mu n 1 2 left rho h n rho right j n rho 1 mu 1 n 2 left rho 1 j n rho 1 right h n rho r ka displaystyle rho ka r1 k1a displaystyle rho 1 k 1 a Bu katsayilarda a displaystyle a kurenin yaricapina jn displaystyle j n ile hn displaystyle h n fonksiyonlari da sirasiyla birince tip kuresel Bessel ve Hankel fonksiyonlarina tekabul eder Mie sacilmasi numerik olarak hesaplanirken sonsuz seri toplaminin bir yerden sonra kesilmesi gerekir Bununla ilgili en yaygin kriterlerden biri Wiscombe un kriteridir ve Lmax x 4x1 3 2 displaystyle L max x 4x 1 3 2 terimlerin dogruya yakin sonuclar icin yeterli oldugunu belirtir Bu denklem de x r displaystyle rho ile estir Sacilma ve yok olma tesir kesitleri 100 nm yaricapli bir altin nanokuresinin dalga boyuna gore sacilma tesir kesiti spektrumu Mie teorisinde ve sacilmada etkinlik katsayilari siklikla kullanilan parametrelerdendir Bu katsayilar yok olma Qe displaystyle Q e sacilma Qs displaystyle Q s ve sogurma Qa displaystyle Q a icin tanimlanabilir Bu katsayilar ilgili tesir kesitlerinin isigin sacildigi kurenin kesit alanina oranidir Ornek olarak bir Mie sacilmasinda sacilma etkinlik katsayisi Qs sspa2 displaystyle Q s frac sigma s pi a 2 formulu ile hesaplanabilir bu denklemde ss displaystyle sigma s sacilma tesir kesiti ve a da parcacik yaricapidir Yok olma kesiti Mie teorisinde su sekilde tanimlanir se ss sa displaystyle sigma e sigma s sigma a and Qe Qs Qa displaystyle Q e Q s Q a Gene Mie teorisine gore sacilma ve yok olma katsayilari sonsuz bir seri ile gosterilebilir Qs 2pk2 n 1 2n 1 an 2 bn 2 displaystyle Q s frac 2 pi k 2 sum n 1 infty 2n 1 a n 2 b n 2 Qe 2pk2 n 1 2n 1 ℜ an bn displaystyle Q e frac 2 pi k 2 sum n 1 infty 2n 1 Re a n b n UygulamalarMukemmel iletken bir metal kurenin dalga boyuna gore Mie radar kesiti grafigi Mie teorisi atmosfer biliminde bulut ve tozlardaki isik sacilmasinin incelenmesi icin sikca kullanilmaktadir Teorinin diger kullanim alanlari arasinda biyomedikal sistemler ile radarlar bulunmaktadir Mie sacilimi ayni zamanda bazi metamateryal ve plazmonik yapilarin teorisinde yer edinmistir Kaynakca a b c d e Bohren amp Huffman 2010 s 82 97 Jackson 1998 s 473 478 van de Hulst 1957 a b Maier 2007 a b Bohren amp Huffman 2010 s 82 129 Wiscombe W J 1980 Improved Mie scattering algorithms Applied Optics 19 9 1505 1509 doi 10 1364 AO 19 001505 Survikov ST 2011 Mie Scattering A to Z Guide to Thermodynamics Heat and Mass Transfer and Fluids Engineering Thermopedia doi 10 1615 AtoZ m mie scattering ISBN 978 0 8493 9356 3 Erisim tarihi 28 Ocak 2019 Ye Z Jiang X Wang Z Oct 2012 PDF Journal of Software 7 10 2309 2316 28 Ocak 2019 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 15 Haziran 2020 Zhao Q Zhou J Zhang F L Lippens D 2009 Mie resonance based dielectric metamaterials Materials Today 12 12 60 69 doi 10 1016 S1369 7021 09 70318 9 Halas Naomi J Lal Surbhi Chang Wei Shun Link Stephan Nordlander Peter 2011 Plasmons in strongly coupled metallic nanostructures Chemical Reviews 111 6 3913 3961 doi 10 1021 cr200061k Kitap kaynaklariBohren C F Huffmann D R 2010 Absorption and scattering of light by small particles Ingilizce New York Wiley Interscience ISBN 978 3 527 40664 7 Jackson John David 1998 Classical Electrodynamics Ingilizce New York Wiley ISBN 9780471309321 Maier S A 2007 Plasmonics Fundamentals and applications Ingilizce New York Springer ISBN 9780387378251 van de Hulst H C 1957 Light scattering by small particles Ingilizce New York John Wiley and Sons ISBN 9780486139753 Dis baglantilarSCATTERLIB Isik sacilmasi kodlari koleksiyonu 26 Kasim 2020 tarihinde Wayback Machine sitesinde Online Mie sacilmasi hesaplayicisi 29 Ocak 2020 tarihinde Wayback Machine sitesinde PyMieScatt 21 Ekim 2020 tarihinde Wayback Machine sitesinde Mie sacilmasi Python kodu
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans






















