Miktar endeks sayıları tek bir mal veya hizmet veya belirli bir grup veya hizmet için miktarların zaman içinde değişmelerini incelemek amacıyla hesaplanan her bir zaman birimi (genel olarak her yıl) için tek bir sayı hesaplanmasını kapsayan bir zaman serisi özetleme yöntemidir. İktisat bilimi ve iktisat politikası uygulaması için bazı miktar endeksleri çok önem taşımaktadır. Örneğin, ihracat endeksi ve ithalat endeksi dış ticaret ögelerinin miktarlarının zamanla değişmesini gösteren miktar veya hacim endeks sayıları olurlar.
Ancak hemen de belirtmek gerekir ki fiyat endeks sayıları, özellikle enflasyon göstergeleri oldukları için ve özellikle kapitalist piyasa ekonomileri içinde fiyatların değişmesinin nisbi önemi daha fazla olduğu için daha çok teorik ve pratik ilgi çekmektedir.
Diğer taraftan, istatistik bilim dalı içinde zaman serilerinin özetlenip incelenmesi epeyce ilgi görmüştür ve miktar endeks sayıları ile ilgili teorik ve pratik gelişmeler de, uygulamaya özel olan bir konu olarak, istastik bilim dalı içinde yer almaktadırlar.
Tek mal veya hizmet için miktar endeksleri
Tek bir mal veya hizmet için zaman içinde miktar değişmelerini göstermek için basit miktar endeks sayıları kullanılır.
Basit miktar endeksi
Tek bir mal/hizmet için belirli bir yıl (yani t) için bir temel (baz) (yani 0) yılında olan miktara olan oranını gösterir. Bu oran yüzde kesirli olması istenmediği için normalize edilmekte ve 100 ile çarpılmaktadır. Böylece baz yılı için basit miktar endeks sayısı 100 olarak ifade edilmekte ve diğer endeks sayılar 100 altında ise baza göre düşüş ve 100 üstünde ise baza göre artış ifade etmektedir. Miktar relatifi olarak da adlandırılır.
Formülü
şeklindedir.
: Cari t yılı için basit miktar endeksi;
: Cari t yılındaki miktar;
: Temel (baz) 0 yılındaki miktar.
Basit zincirleme miktar endeksi
Bu çeşit miktar endeksinin amacı bir önceki zaman birimine (genellikle yıla) oranla miktar değişimini göstermektir. Miktarın zamanda yıllık değişmelerini incelemek yani her bir yıl için miktar bir önceki yıla ait miktarına bölünür ve bu oran normalize edilmek için 100 ile çarpılır.
Formülü
şeklindedir.
: Cari t yılı için zincirleme miktar endeksi;
: Cari t yılındaki miktar;
: Cari yıldan bir önceki yıldaki miktar.
Bu formül kullanılarak hesaplanan miktar endeksleri eğer 100 ise bir yılda hiç miktar değişmediğini; 100un altında ise geçen yıla göre miktarın azaldığını; 100un üstünde ise bir yılda miktarın arttığını gösterir. Bu basit zincirleme miktar endeks sayları için bir seri yıllık miktar değişmelerinin özet halinde incelenmesine yaramaktadır.
Tek mal/hizmet için miktar endeks sayıları için örnek
Örnek 1: Tek bir mal için 2000 yılından itibaren 2002 yıl bazlı (yani 2002=100) basit miktar endeks sayıları ve basit zincirleme miktar endeks sayıları hesaplanıp şu tablo elde edilir:
| Yıl | Miktar | Basit miktar endeksi (2002=100) | Zincirleme miktar endeksi |
|---|---|---|---|
| 2000 | 400 | 94,121 | - |
| 2001 | 379 | 89,18 | 94,75 |
| 2002 | 425 | 100 | 112,14 |
| 2003 | 510 | 120 | 120 |
| 2004 | 525 | 123,53 | 102,94 |
| 2005 | 600 | 141,18 | 114,29 |
Çok mal veya hizmet için miktar endeks sayıları
İçinde birden fazla mal veya hizmet içeren bir mal veya hizmet grubu için bileşik miktarların zaman içinde değişmesini gösteren bir endeks sayılar serisi çeşididir. Örneğin her birinci sınıf birinci sömestr için kullanılan 5 çeşit ders kitabı için hazırlanan tek bileşik bir miktar endeks serisi üniversite birinci sınıf birinci sömestr ders kitabı satış miktarının zaman içinde nasıl değiştiğini gösterir. Her bir yıl tek bir miktar endeks sayısı hesaplanır ve amaç bu tek miktar endeks sayısının zaman içinde değişmesini incelemektir.
Bu tip miktar endeks sayılarının hazırlanmasında kullanılan ana prensip tek bir standart fiyat listesinin belirlenmesidir. Bu tek standart fiyat listesi içinde bulunan her bir fiyat o mal/hizmetin grup içinde önemini veya ağırlığını ifade eder. Her cari yıl için miktar endeks sayısını hesaplamak için önce standart fiyat listesi içinde bulunan fiyatlar cari yıl miktarları çarpılıp tüm mal/hizmetler için toplanıp, cari yıl için standart yıl fiyatlarına göre bir değer elde edilir. Sonra yine standart fiyat listesi fiyatları ile temel (baz) yıl miktarları çarpılıp bunlar toplanıp bir diğer değer elde edilir. Bulunan toplam iki değerinin oranı cari yıl için miktar endeks sayısı olur. Standard fiyat listesinde hangi yıl fiyatları kullanılacağına göre iki değişik tip miktar endeks sayısı hesaplanabilir.
Temel yıl ağırlıklı Laspeyres miktar endeksi
Bu miktar indeksinde sadece temel (baz) yıl ait fiyatlar (yani 

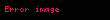

t yılı için Laspeyres Miktar Endeksi 
şeklindedir. Burada
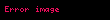


Grup içinde bulunan i (1'den n'ye kadar) mal ve hizmetleri üzerinde yapılan toplama işlemi 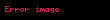
Bu formülden görülür ki her yıl için yapılan hesapta oranın paydası (temel yılın miktarları ve temel yıl fiyat listesi ile değerlendirilmesi olduğu için) yıldan yıla değişmemekte ve her yıl için aynı kalmaktadır. Böylece sadece tek bir fiyat listesi, yani sadece yani temel yıla ait fiyatlar, bulunması yeterli olmakta ve her yıl için yeni bir fiyat listesi yapma gereği bulunmamaktadır. Bu karakteristik miktar endeks sayılarının hesaplanmasında Laspeyres formülünün bir avantajı sayılmaktadır. Diğer taraftan, eğer enflasyon hızı yüksek ise ve baz yılı çok eskide kalıp mallar karakter değiştirip ve yeni mallar önem kazanmışsa, baz yılına ait fiyat listesi mal/hizmetlerin cari yıldaki önemini yansıtmayacaktır.
Cari yıl ağırlıklı Paasche miktar endeksi
Bu çeşit miktar indeksinde ise standart fiyat listesi (yani kullanılan fiyat ağırlıkları) cari yıla aittir. Cari yıldaki endeksi bulmak için önce cari yıl fiyat listesi kullanılarak cari miktarlar ile çarpılıp değerler elde edilip bu değerlerin toplamı (yani 


t yılı için Paasche Miktar Endeksi 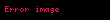
şeklindedir. Burada
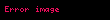


Grup içinde bulunan tüm i (1'den n'ye kadar) mal ve hizmetleri üzerinde yapılan toplama işlemi 
Paasche miktar endeks sayıları' elde edilmesi için her yıl değişik bir standart fiyat listesi (ağırlıklar) kullanılmaktadır. Eğer bu yıldan yıla değişen ağırlıklar (standart fiyat listesi) kendi aralarında zaman içinde sistematik bir değişme gösterirlerse, elde edilen miktar endeks sayıları sadece miktar değişmelerini değil, kullanılan standart fiyat listelerindeki sistematik değişikliği de yansıtacaklardır.
Çok mal veya hizmet için miktar endeks sayıları için örnek
Örnek 2: Dört malı kapsayan bir bileşik mal grubu için 2000 yılından itibaren fiyatlar ve miktarlar ve 2002 yıl bazlı Laspayres miktar endeks sayıları ve Paasche miktar endeks sayıları hesaplanıp şu tablolarda gösterilmektedir:
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Miktar endeks sayilari tek bir mal veya hizmet veya belirli bir grup veya hizmet icin miktarlarin zaman icinde degismelerini incelemek amaciyla hesaplanan her bir zaman birimi genel olarak her yil icin tek bir sayi hesaplanmasini kapsayan bir zaman serisi ozetleme yontemidir Iktisat bilimi ve iktisat politikasi uygulamasi icin bazi miktar endeksleri cok onem tasimaktadir Ornegin ihracat endeksi ve ithalat endeksi dis ticaret ogelerinin miktarlarinin zamanla degismesini gosteren miktar veya hacim endeks sayilari olurlar Ancak hemen de belirtmek gerekir ki fiyat endeks sayilari ozellikle enflasyon gostergeleri olduklari icin ve ozellikle kapitalist piyasa ekonomileri icinde fiyatlarin degismesinin nisbi onemi daha fazla oldugu icin daha cok teorik ve pratik ilgi cekmektedir Diger taraftan istatistik bilim dali icinde zaman serilerinin ozetlenip incelenmesi epeyce ilgi gormustur ve miktar endeks sayilari ile ilgili teorik ve pratik gelismeler de uygulamaya ozel olan bir konu olarak istastik bilim dali icinde yer almaktadirlar Tek mal veya hizmet icin miktar endeksleriTek bir mal veya hizmet icin zaman icinde miktar degismelerini gostermek icin basit miktar endeks sayilari kullanilir Basit miktar endeksi Tek bir mal hizmet icin belirli bir yil yani t icin bir temel baz yani 0 yilinda olan miktara olan oranini gosterir Bu oran yuzde kesirli olmasi istenmedigi icin normalize edilmekte ve 100 ile carpilmaktadir Boylece baz yili icin basit miktar endeks sayisi 100 olarak ifade edilmekte ve diger endeks sayilar 100 altinda ise baza gore dusus ve 100 ustunde ise baza gore artis ifade etmektedir Miktar relatifi olarak da adlandirilir Formulu MIt qtq0 100 displaystyle MI t frac q t q 0 times 100 seklindedir MIt displaystyle MI t Cari t yili icin basit miktar endeksi qt displaystyle q t Cari t yilindaki miktar q0 displaystyle q 0 Temel baz 0 yilindaki miktar Basit zincirleme miktar endeksi Bu cesit miktar endeksinin amaci bir onceki zaman birimine genellikle yila oranla miktar degisimini gostermektir Miktarin zamanda yillik degismelerini incelemek yani her bir yil icin miktar bir onceki yila ait miktarina bolunur ve bu oran normalize edilmek icin 100 ile carpilir Formulu MIt qtqt 1 100 displaystyle MI t frac q t q t 1 times 100 seklindedir MIt displaystyle MI t Cari t yili icin zincirleme miktar endeksi qt displaystyle q t Cari t yilindaki miktar qt 1 displaystyle q t 1 Cari yildan bir onceki yildaki miktar Bu formul kullanilarak hesaplanan miktar endeksleri eger 100 ise bir yilda hic miktar degismedigini 100un altinda ise gecen yila gore miktarin azaldigini 100un ustunde ise bir yilda miktarin arttigini gosterir Bu basit zincirleme miktar endeks saylari icin bir seri yillik miktar degismelerinin ozet halinde incelenmesine yaramaktadir Tek mal hizmet icin miktar endeks sayilari icin ornek Ornek 1 Tek bir mal icin 2000 yilindan itibaren 2002 yil bazli yani 2002 100 basit miktar endeks sayilari ve basit zincirleme miktar endeks sayilari hesaplanip su tablo elde edilir Yil Miktar Basit miktar endeksi 2002 100 Zincirleme miktar endeksi2000 400 94 121 2001 379 89 18 94 752002 425 100 112 142003 510 120 1202004 525 123 53 102 942005 600 141 18 114 29Cok mal veya hizmet icin miktar endeks sayilariIcinde birden fazla mal veya hizmet iceren bir mal veya hizmet grubu icin bilesik miktarlarin zaman icinde degismesini gosteren bir endeks sayilar serisi cesididir Ornegin her birinci sinif birinci somestr icin kullanilan 5 cesit ders kitabi icin hazirlanan tek bilesik bir miktar endeks serisi universite birinci sinif birinci somestr ders kitabi satis miktarinin zaman icinde nasil degistigini gosterir Her bir yil tek bir miktar endeks sayisi hesaplanir ve amac bu tek miktar endeks sayisinin zaman icinde degismesini incelemektir Bu tip miktar endeks sayilarinin hazirlanmasinda kullanilan ana prensip tek bir standart fiyat listesinin belirlenmesidir Bu tek standart fiyat listesi icinde bulunan her bir fiyat o mal hizmetin grup icinde onemini veya agirligini ifade eder Her cari yil icin miktar endeks sayisini hesaplamak icin once standart fiyat listesi icinde bulunan fiyatlar cari yil miktarlari carpilip tum mal hizmetler icin toplanip cari yil icin standart yil fiyatlarina gore bir deger elde edilir Sonra yine standart fiyat listesi fiyatlari ile temel baz yil miktarlari carpilip bunlar toplanip bir diger deger elde edilir Bulunan toplam iki degerinin orani cari yil icin miktar endeks sayisi olur Standard fiyat listesinde hangi yil fiyatlari kullanilacagina gore iki degisik tip miktar endeks sayisi hesaplanabilir Temel yil agirlikli Laspeyres miktar endeksi Bu miktar indeksinde sadece temel baz yil ait fiyatlar yani pi0 displaystyle p i0 i 1 n standart fiyat listesine konulur Her cari yil icin her bir miktar yani qit displaystyle q it temel yilina ait fiyat ile carpilir ve bu carpimlarin tum mal hizmetler icin toplami yani i 1nqit pi0 displaystyle sum i 1 n q it p i0 cari yil icin tek bir deger ortaya cikartir Yine ayni temel yili fiyat listesindeki fiyatlar temel yil miktarlari ile carpilip tum mal hizmetler icin toplanarak bir diger deger yani i 1nqi0 pi0 displaystyle sum i 1 n q i0 p i0 elde edilir Bu iki deger orani Laspeyres Miktar Endeksi ni olusturur Dikkat edilirse miktar endeks sayilari iki degerin miktarin degil oranidir Ama bu oranin pay ve paydasinda bulunan fiyatlar listesi yani pi0 displaystyle p i0 i 1 n degismemektedir ve hem pay hem paydada baz yili fiyatlari olarak kalirlar Pay ve paydada bulunan miktarlar degistigi icin iki degerinin orani miktar degismelerinin bir agirlikli ortalama ozetini verir t yili icin Laspeyres Miktar Endeksi MILt displaystyle MI Lt icin formul MILt i 1nqit pi0 i 1nqi0 pi0 100 displaystyle MI Lt frac sum i 1 n q it p i0 sum i 1 n q i0 p i0 times 100 seklindedir Burada qit displaystyle q it i mal hizmeti icin cari t yilindaki miktarlar pi0 displaystyle p i0 i mal hizmeti icin temel 0 yilindaki fiyatlar qi0 displaystyle q i0 i mal hizmeti icin temel 0 yilindaki miktarlar Grup icinde bulunan i 1 den n ye kadar mal ve hizmetleri uzerinde yapilan toplama islemi i 1n displaystyle sum i 1 n ile ifade edilmekte ve 100 ile carpma ise indeksin normalize edilip 1 yerine 100 olmasini saglamaktadir Bu formulden gorulur ki her yil icin yapilan hesapta oranin paydasi temel yilin miktarlari ve temel yil fiyat listesi ile degerlendirilmesi oldugu icin yildan yila degismemekte ve her yil icin ayni kalmaktadir Boylece sadece tek bir fiyat listesi yani sadece yani temel yila ait fiyatlar bulunmasi yeterli olmakta ve her yil icin yeni bir fiyat listesi yapma geregi bulunmamaktadir Bu karakteristik miktar endeks sayilarinin hesaplanmasinda Laspeyres formulunun bir avantaji sayilmaktadir Diger taraftan eger enflasyon hizi yuksek ise ve baz yili cok eskide kalip mallar karakter degistirip ve yeni mallar onem kazanmissa baz yilina ait fiyat listesi mal hizmetlerin cari yildaki onemini yansitmayacaktir Cari yil agirlikli Paasche miktar endeksi Bu cesit miktar indeksinde ise standart fiyat listesi yani kullanilan fiyat agirliklari cari yila aittir Cari yildaki endeksi bulmak icin once cari yil fiyat listesi kullanilarak cari miktarlar ile carpilip degerler elde edilip bu degerlerin toplami yani i 1nqit pit displaystyle sum i 1 n q it p it tek bir pay degeri olarak elde edilir Yine cari yil fiyat listesi kullanilarak temel yil miktarlari ile carpilip degerler bulunup hepsi toplaninca bir payda degeri yani i 1nqi0 pit displaystyle sum i 1 n q i0 p it bulunur Bu pay degeri ile payda degeri orani o cari yil icin Paasche miktar indeksi olur Yine gorulmektedir ki hem pay hem payda degerdir ancak pay ve payda da kullanilan cari fiyatlar listesi yani pit displaystyle p it i 1 n aynidir Bu demektir ki oran miktar degismelerini yansitir t yili icin Paasche Miktar Endeksi MIPt displaystyle MI Pt icin formul MIPt i 1nqit pit i 1nqi0 pit 100 displaystyle MI Pt frac sum i 1 n q it p it sum i 1 n q i0 p it times 100 seklindedir Burada qit displaystyle q it i mal hizmeti icin cari t yilindaki miktarlar pit displaystyle p it i mal hizmeti icin cari t yilindaki fiyatlar qi0 displaystyle q i0 i mal hizmeti icin temel 0 yilindaki miktarlar Grup icinde bulunan tum i 1 den n ye kadar mal ve hizmetleri uzerinde yapilan toplama islemi i 1n displaystyle sum i 1 n ile ifade edilmekte ve 100 ile carpma ise indeksin normalize edilip 1 yerine 100 olmasini saglamaktadir Paasche miktar endeks sayilari elde edilmesi icin her yil degisik bir standart fiyat listesi agirliklar kullanilmaktadir Eger bu yildan yila degisen agirliklar standart fiyat listesi kendi aralarinda zaman icinde sistematik bir degisme gosterirlerse elde edilen miktar endeks sayilari sadece miktar degismelerini degil kullanilan standart fiyat listelerindeki sistematik degisikligi de yansitacaklardir Cok mal veya hizmet icin miktar endeks sayilari icin ornek Ornek 2 Dort mali kapsayan bir bilesik mal grubu icin 2000 yilindan itibaren fiyatlar ve miktarlar ve 2002 yil bazli Laspayres miktar endeks sayilari ve Paasche miktar endeks sayilari hesaplanip su tablolarda gosterilmektedir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans