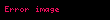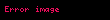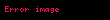Minkowski EĆitsizliÄi, sonlu sayıda, hepsi sıfır olmayan , , i=1,2,...,n pozitif sayılarında, p>1 için aĆaÄıdaki eĆitsizliÄe denir:
Hölder EĆitsizliÄinden tĂŒretilebilen, uygulamada oldukça yararlı bu eĆitsizliÄi Alman matematikçi Hermann Minkowski (1864-1909) elde etmiĆtir.
ĂŒĂ§gen'de, Minkowski eĆitsizliÄi' ' belirlemesidir. diyelimki S bir olsun,ve diyelimki 1 †p †â ve diyelimki Lp(S) ögeleri f ve g olsun. ise Lp(S) içindeki f + gdir ve bizim ĂŒĂ§gen eĆitsizliÄi'miz var
için eĆitliÄi ile 1 < p <â eÄer ve yalnızca eÄerf ve g pozitifliÄi , yani burada bazı â„ 0.için f = g aĆaÄıdaki norm ile verilir:
EÄer p < â veya p = â durumu içinde ile
Minkowski eĆitsizliÄi Lp(S) içinde ĂŒĂ§gen eĆitsizliÄidir,aslında bu durumun daha genel durumu var,
bunun saÄ-el tarafta ĂŒĂ§gen eĆitsizliÄinin tatmin edici olduÄunu görmek kolay
Hölder eĆitsizliÄi gibi,Minkowski eĆitsizliÄi dizisi özelleĆtirilebilir ve vektörler tarafından kullanılıyor:
için tĂŒmgerçel (veya karmaĆık) x1, ..., xn, y1, ..., yn sayıları için ve burada n ;S'in 'sidir. (S'in ögelerinin sayısı).
Kanıt
Ä°lk, kanıtı f+g sonludur p-norm eÄer f ve g ikilisi olarak, bunlar ile aĆaÄıda
Nitekim, aslında burada 
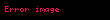

Bunun anlamı
Ćimdi, yasal olarak konuĆabiliriz 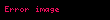
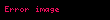
Biz elde Minkowski'nin eĆitsizliÄi ile 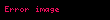
Minkowski integral eĆitsizliÄi
Varsayalımki (S1,ÎŒ1) ve (S2,ÎŒ2) are iki ölĂ§ĂŒm uzayıs ve F : S1ĂS2 â R ölĂ§ĂŒlebilirdir. ise Minkowski's integral eĆitsizliÄi is Stein 1970, §A.1dir, Hardy, Littlewood & PĂłlya 1988, Theorem 202:
durumunda belirgin deÄiĆiklikler p = â. eÄer p > 1 ve her iki taraf sonlu, ise eĆitlikle örtĂŒĆĂŒr eÄer |F(x,y)| = Ï(x)Ï(y) a.e.bazı negatif ölĂ§ĂŒlebilir fonksiyonlar Ï ve Ï için.
EÄer ÎŒ1 iki nokta kĂŒmesi sayma ölĂ§ĂŒsĂŒS1 = {1,2}, ise Minkowski eĆitsizliÄi bir özel durum olarak verir: için Æi(y) = F(i,y) yapıĆtırma için i = 1,2, integral eĆitsizliÄini verir.
Ayrıca bakınız
Kaynakça
- Hardy, G. H.; Littlewood, J. E.; PĂłlya, G. (1952). "Inequalities". 2. Cambridge: Cambridge University Press. ISBNÂ .
- Minkowski, H. (1953). "Geometrie der Zahlen". Chelsea.
- (1970). "Singular integrals ve differentiability properties of functions". Princeton University Press.
- Hazewinkel, Michiel, (Ed.) (2001), "Minkowski eĆitsizliÄi", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBNÂ
- Arthur Lohwater (1982). "Introduction to Inequalities" (PDF, Online e-book). mediafire.com. 14 Ekim 2012 tarihinde kaynaÄından . EriĆim tarihi: 27 Ekim 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kĂŒtĂŒphane, kĂŒtĂŒbhane, ara, ara bul, bul, herĆey, ne arasanız burada,hikayeler, makale, kitaplar, öÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tĂŒrk, tĂŒrkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ĂŒcretsiz, ĂŒcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mĂŒzik, Ćarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Minkowski Esitsizligi sonlu sayida hepsi sifir olmayan ai displaystyle a i bi displaystyle b i i 1 2 n pozitif sayilarinda p gt 1 icin asagidaki esitsizlige denir i 1n ai bi p 1 p i 1naip 1 p i 1nbip 1 p displaystyle left sum i 1 n a i b i p right 1 p leq left sum i 1 n a i p right 1 p left sum i 1 n b i p right 1 p Holder Esitsizliginden turetilebilen uygulamada oldukca yararli bu esitsizligi Alman matematikci Hermann Minkowski 1864 1909 elde etmistir ucgen de Minkowski esitsizligi belirlemesidir diyelimki S bir olsun ve diyelimki 1 p ve diyelimki Lp S ogeleri f ve g olsun ise Lp S icindeki f gdir ve bizim ucgen esitsizligi miz var f g p f p g p displaystyle f g p leq f p g p icin esitligi ile 1 lt p lt eger ve yalnizca egerf ve g pozitifligi yani burada bazi l displaystyle lambda 0 icin f l displaystyle lambda g asagidaki norm ile verilir f p f pdm 1 p displaystyle f p left int f p d mu right 1 p Eger p lt veya p durumu icinde ile f ess supx S f x displaystyle f infty operatorname ess sup x in S f x Minkowski esitsizligi Lp S icinde ucgen esitsizligidir aslinda bu durumun daha genel durumu var f p sup g q 1 fg dm 1 p 1 q 1 displaystyle f p sup g q 1 int fg d mu qquad 1 p 1 q 1 bunun sag el tarafta ucgen esitsizliginin tatmin edici oldugunu gormek kolay Holder esitsizligi gibi Minkowski esitsizligi dizisi ozellestirilebilir ve vektorler tarafindan kullaniliyor k 1n xk yk p 1 p k 1n xk p 1 p k 1n yk p 1 p displaystyle left sum k 1 n x k y k p right 1 p leq left sum k 1 n x k p right 1 p left sum k 1 n y k p right 1 p icin tumgercel veya karmasik x1 xn y1 yn sayilari icin ve burada n S in sidir S in ogelerinin sayisi KanitIlk kaniti f g sonludur p norm eger f ve g ikilisi olarak bunlar ile asagida f g p 2p 1 f p g p displaystyle f g p leq 2 p 1 f p g p Nitekim aslinda burada h x xp displaystyle h x x p uzerinde R displaystyle mathbb R p displaystyle p birden buyuk icin ve yine konveksite tanimi ile 12f 12g p 12 f 12 g p 12 f p 12 g p displaystyle left frac 1 2 f frac 1 2 g right p leq left frac 1 2 f frac 1 2 g right p leq frac 1 2 f p frac 1 2 g p Bunun anlami f g p 12 2f p 12 2g p 2p 1 f p 2p 1 g p displaystyle f g p leq frac 1 2 2f p frac 1 2 2g p 2 p 1 f p 2 p 1 g p Simdi yasal olarak konusabiliriz f g p displaystyle f g p Sifir ise Minkowski esitsizligi tutar Simdi varsayalim ki f g p displaystyle f g p sifir degildir kullaniliyor f g pp f g pdm displaystyle f g p p int f g p mathrm d mu f g f g p 1dm displaystyle leq int f g f g p 1 mathrm d mu f f g p 1dm g f g p 1dm displaystyle int f f g p 1 mathrm d mu int g f g p 1 mathrm d mu Ho lder f pdm 1 p g pdm 1 p f g p 1 pp 1 dm 1 1p displaystyle stackrel text H ddot text o text lder leq left left int f p mathrm d mu right 1 p left int g p mathrm d mu right 1 p right left int f g p 1 left frac p p 1 right mathrm d mu right 1 frac 1 p f p g p f g pp f g p displaystyle f p g p frac f g p p f g p Biz elde Minkowski nin esitsizligi ile f g p f g pp displaystyle frac f g p f g p p her iki taraf carparizMinkowski integral esitsizligiVarsayalimki S1 m1 ve S2 m2 are iki olcum uzayis ve F S1 S2 R olculebilirdir ise Minkowski s integral esitsizligi is Stein 1970 A 1dir Hardy Littlewood amp Polya 1988 Theorem 202 S2 S1F x y dm1 x pdm2 y 1 p S1 S2 F x y pdm2 y 1 pdm1 x displaystyle left int S 2 left int S 1 F x y d mu 1 x right p d mu 2 y right 1 p leq int S 1 left int S 2 F x y p d mu 2 y right 1 p d mu 1 x durumunda belirgin degisiklikler p eger p gt 1 ve her iki taraf sonlu ise esitlikle ortusur eger F x y f x ps y a e bazi negatif olculebilir fonksiyonlar f ve ps icin Eger m1 iki nokta kumesi sayma olcusuS1 1 2 ise Minkowski esitsizligi bir ozel durum olarak verir icin Æi y F i y yapistirma icin i 1 2 integral esitsizligini verir f1 f2 p S2 S1F x y dm1 x pdm2 y 1 p S1 S2 F x y pdm2 y 1 pdm1 x f1 p f2 p displaystyle begin aligned f 1 f 2 p amp left int S 2 left int S 1 F x y d mu 1 x right p d mu 2 y right 1 p leq int S 1 left int S 2 F x y p d mu 2 y right 1 p d mu 1 x f 1 p f 2 p end aligned Ayrica bakinizMahler esitsizligi Holder esitsizligiKaynakcaHardy G H Littlewood J E Polya G 1952 Inequalities 2 Cambridge Cambridge University Press ISBN 0 521 35880 9 Eksik ya da bos url yardim Minkowski H 1953 Geometrie der Zahlen Chelsea 1970 Singular integrals ve differentiability properties of functions Princeton University Press Hazewinkel Michiel Ed 2001 Minkowski esitsizligi Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Arthur Lohwater 1982 Introduction to Inequalities PDF Online e book mediafire com 14 Ekim 2012 tarihinde kaynagindan Erisim tarihi 27 Ekim 2013
 AzÉrbaycanca
AzÉrbaycanca ĐДлаŃŃŃĐșŃ
ĐДлаŃŃŃĐșŃ Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana æ„æŹèȘ
æ„æŹèȘ ÒĐ°Đ·Đ°Ò
ÒĐ°Đ·Đ°Ò Lietuvos
Lietuvos Nederlands
Nederlands PortuguĂȘs
PortuguĂȘs Đ ŃŃŃĐșĐžĐč
Đ ŃŃŃĐșĐžĐč à·à·à¶à·à¶œ
à·à·à¶à·à¶œ àčàžàžàčàžàžą
àčàžàžàčàžàžą TĂŒrkçe
TĂŒrkçe ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ°
ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ° äžćäșș
äžćäșș United State
United State Afrikaans
Afrikaans