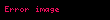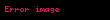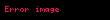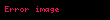Minkowski mesafesi Öklid uzayı'nda bir 'tir iki ve 'nin bir genelleştirilmesi ile oluşturulur.
Tanım
p iki nokta arası yerine Minkowski mesafesi(uzalığı)
aşağıdaki şekilde tanımlanır:
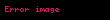
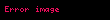
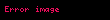
Minkowski uzaklığı tipik kullanımı ile p olarak 1 veya 2'dir . ikincisi 'dir, önceki bazen olarak da bilinir.pnin sonsuza ulaşrken limitinin, eldesi :
Benzer şekilde, p nin negatif sonsuza ulaşanı,için elimizde:
var. Minkowski mesafesi birçoğul 'ün P ve Q akıllı-bileşen arası farkı olarak da görülebilir.
p nin çeşitli değerleri ile birim çemberi gösteren görsel aşağıdadır :

Ayrıca bakınız
Dış bağlantılar
Simple IEEE 754 implementation in C++ 15 Kasım 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Minkowski mesafesi Oklid uzayi nda bir tir iki ve nin bir genellestirilmesi ile olusturulur Tanimp iki nokta arasi yerine Minkowski mesafesi uzaligi P x1 x2 xn and Q y1 y2 yn Rn displaystyle P x 1 x 2 ldots x n text and Q y 1 y 2 ldots y n in mathbb R n asagidaki sekilde tanimlanir i 1n xi yi p 1 p displaystyle left sum i 1 n x i y i p right 1 p p 1 displaystyle p geq 1 icin Minkowski mesafesi bir Minkowski esitsizligi nin bir sonucudur p lt 1 displaystyle p lt 1 icin degil 0 0 ve 1 1 arasindaki mesafe 21 p gt 2 displaystyle 2 1 p gt 2 ama nokta 0 1 bu iki nokta arasinda bir mesafe 1 dir Bu nedenle bu ucgen esitsizligi ni ihlal eder Minkowski uzakligi tipik kullanimi ile p olarak 1 veya 2 dir ikincisi dir onceki bazen olarak da bilinir pnin sonsuza ulasrken limitinin eldesi limp i 1n xi yi p 1p maxi 1n xi yi displaystyle lim p to infty left sum i 1 n x i y i p right frac 1 p max i 1 n x i y i Benzer sekilde p nin negatif sonsuza ulasani icin elimizde limp i 1n xi yi p 1p mini 1n xi yi displaystyle lim p to infty left sum i 1 n x i y i p right frac 1 p min i 1 n x i y i var Minkowski mesafesi bircogul un PveQakilli bilesen arasi farki olarak da gorulebilir p nin cesitli degerleri ile birim cemberi gosteren gorsel asagidadir Ayrica bakinizDis baglantilarSimple IEEE 754 implementation in C 15 Kasim 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State