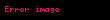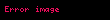Matematikte, monstrous moonshine ve moonshine teorisi terimleri John Horton Conway ve Simon P. Norton tarafından düşünülmüştür. Zamanında, monster grup ve modüler fonksiyonlar arasındaki beklenmedik bağıntıyı tanımlamak için kullanılmıştır. Şu an biliniyor ki, monstrous moonshine'nın altında yatan, simetriler gibi monster grup içeren conformal field teorisidir. Varsayımlar Conway ve Norton tarafından yapıldı ve 1992 yılında ispatıda Richard Borcherds tarafından, string teori, vertex operatör cebiri teorisi ve genişletilmiş Kac–Moody cebirinden no-ghost teoremini kullanılarak yapılmıştır.
Tarihi
1978 yılında, John McKay, 'nın Fourier açılımının ilk birkaç terimin,
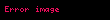
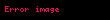
(rn arasında birden çok lineer bağıntı olabileceğinden, örnek olarak 
Conway and Norton, bu tarz kademeli ilkköşegen toplamlarını hesaplamışlardı, şimdi McKay–Thompson Tg serileri olarak bilinen yapıları ve hepsinin Hauptmoduln'nın açılımları olduğunu bulmuşlardı. Bir başka deyişle, eğer Gg, 'nın bir altkümesiyse ki bu Tyi düzeltir, o zaman karışık düzlemin upper half'ının quotient'ası G için, bir küredir, sonlu sayıda sayının silinmesiyle ve buna ek olarak T, Meromorf fonksiyonunun cismini üretir bu küre üzerinde.
Ölçümlerine dayanak, Conway ve Norton bir Hauptmoduln listesi oluşturdu ve olabileceği Mnin kademeli sunumunun sonsuz boyutluluğunun mevcudiyetinin olabileceği öngörüsünde bulundular. Bunun kademeli ilkköşegen toplamları Tg, tam olarak yaptıkları listedeki fonksiyonların açılımlarıydı.
1980 yılında, A. Oliver L. Atkin, Paul Fong ve Stephen D. Smith böyle kademeli gösterimimlerinin mümkün olabileceğini gösterdi, bilgisayar hesap makineleri kullanarak bir sınıra kadar j katsayılarının m gösterimi Thompson tarafından zaten ispatlanmıştı. kademeli gösterimi bariz bir şekilde Igor Frenkel, James Lepowsky, and Arne Meurman tarafından, etkileyici bir çözüm verilerek McKay–Thompson varsayımına, inşa edilmiştir. Buna ek olarak, onların inşa ettiği vektör uzayı Moonshine Module diye adlandırılan, vertex operatör cebirinin fazldan bir yapısı vardır. Ve bu yapının automorphism grubu tam olarak M idi.
Borcherds, Conway–Norton varsayımını 1992 yılında kanıtladı, Moonshine Module için. Fields madalyasını kazandı 1998 yılında varsayımı çözdüğü kısım için.
The Monster modülü
Frenkel–Lepowsky–Meurman yapısının iki temel araç kullanır;
- Lattice vertex operatör cebiri yapısı VL, n rankın lattice L için olsa bile. Fiziksel anlamda, için simit şekli üstünde VL, lattice vertex operatörü chiral cebiridir, Bosonic string kompaktlaştırılmasıyla. "n" boyuttaki Osilatör gösterimiyle, hemen hemen tanımlanabilir, L'nin group ring'nin tensor product'ı olarak (ki bu demektir ki, sonsuz çoklukta jeneratör durumu için polynomial ring isomorphictir). Sorudaki durum için, L kümesinin Leech lattice olacak şekilde ayarlanması gerekir, 24 rankı olan.
- İkinci araç orbifold yapısı diye adlandırılır. Fiziksel anlamda, orbifold'un temsil ettiği bosonic string salınımlarıdır quotient orbifold üstünde. Frenkel–Lepowsky–Meurman yapısı, conformal field teoride ilk ortaya çıkan orbifoldlardır. Leech lattice'nin tersine fonksiyonel olarak bağımlı olan VL'nın "h"'sıdir. Moonshine modülünü elde etmek için, "h"'nin sabit bir noktası seçilir, "V"'nın direkt toplamlarında ve onun twisted modülünü alır.
Frenkel, Lepowsky ve Meurman gösterdi ki moonshine modülünün automorphism grupları, vertex operatör cebir olanları, "M"'dir ve kademeli boyut "j"'nın bir Fourier serisi açılımı verir. (Frenkel, Lepowsky & Meurman (1988)).
Borcherds'in ispatı
Conway and Norton'nın öngörüsüne olan Richard Borcherds'nın ispatı 6 parçada anlatılabilinir;
- Otomorfizmler kullanarak "M"'e yapılan bir hamle ve kademeli boyutlu j ile, Vertex operatör cebiri olan V'i seçerek başlanır. Moonshine Module tarafından sağlanmıştır, ayrıca monster vertex cebiri diye de adlandırılır.
- Lie cebiri
, monster Lie cebiri diye adlandırılan, kuantalama fonktörü kullanılarak yapılandırılmıştır. Bu genelleştirilmiş Kac–Moody cebiridir, otomorfizm'i kullanarak Monster hamlesinden.
- Genelleştirilmiş Kac–Moody Lie cebirini oluşturmak için Koike–Norton–Zagier sonsuz çarpım özdeşliği kullanılır. Özdeşlik Hecke operetörü kullanarak sağlanmıştır.
- Kök çeşitliliği karşılaştırılarak, Lie cebirlerinin izomorf olduğu bulunabilinir. Benzer yolla, Weyl bölen formülü,
için tam olarak Koike–Norton–Zagier özdeşliğine denktir.
- kullanarak ve Adams operatörlerini, twisted bölün özdeşliği her eleman için verilir. Bu özdeşlikler McKay–Thompson serileriyle bağlantılıdırlar, Koike–Norton–Zagier özdeşlikleriyle bağlantılı oldukları gibi.
- Twisted bölen özdeşliği, yineleme ilişkilerini ima eder Tg'nın katsayıları üstünde. Bu ilişkiler o kadar güçlüdür ki sadece Conway and Norton tarafından verilen bir fonksiyonla ilk yedi terimin sağlanması yeter.
Böylelikle, ispat tamamlanmıştır. (Borcherds (1992)). Borcherds, sonraları bu ispatı şu sözleriyle anmıştır; "Ben Ay'ın ötesindeydim, moonshine sanısını ispatlıyorken. Ve bazen merak ediyorum, eğer belirli ilaçlar alındığında hissedilen, ben ispatlarken hissettiklerimse, ama gerçekten bilmiyorum, çünkü daha o teorimi test etmedim."
Genelleştirilmiş Moonshine
Conway ve Norton, 1979 yılında yazdıkları makalede moonshine'nın monster ile sınırlı olmayabileceğini belirttiler, ama bu fenomen başka gruplar için bulunabilinir.
- T1A ve M
- T2A ve F2
- T2B ve
- T3A ve Fi23, Fi24
- T3C ve Th = F3
- T4A ve
- T4A ve McL
- T5A ve HN = F5
- T6A ve Fi22
- T6B ve Suz
- T7A ve He = F7
- T10A ve HS
1980 yılında, Sporadic gruplarının boyutlarının basit kombinaslonları kullanılarak birçok McKay-Thompson(Hauptmodul) serisinin açılabilecek şekilde inşa edilebileceğini buldu, Larissa Queen ve diğerleri. Genelleştirilmiş Moonshine sanısını formüle etmek için, Norton kendi hesaplamalarını Queen'ninkilerle karşılaştırdı, 1987 yılında. Monster'ın her g elemanı, kademeli vektör uzayı V(g) ve upper-half düzleminde Holomorf fonksiyonunun f(g,h,τ) her (g,h) elemanını değiştiren için aşağıdaki şartların sağlanabileceğini öne sürer bu sanı;
- Her V(g), g'nin merkezleyicisinin kademeli izdüşümsel gösterimidir.
- Her f(g,h,τ), ya sabit bir fonksiyon veyahut Hauptmodul'dur.
- Her f(g,h,τ), "M"'de "g" ve "h"'nin eşzamanlı konjügasyonun altında sabit niceliğidir.
- Her (g,h) için, V(g) üstünde bir doğrusal dönüşüm vardır.
- Herhangi bir
için
,
'ye doğru orantılıdır.
- Eğer g = h = 1. ise, f(g,h,τ), j ye doğru orantılıdır.
Bu Conway–Norton sanısının geneleştirilmiş halidir, çünkü Borcherds'nin teoremi, eğer g bir birim kümesi olduğu durumla ilgililenir. Şu an hala, bu sanası hala sadece bir sanıdır.
Conway–Norton sanısında olduğu gibi, Genelleştirilmiş Moonshine'nında fizikte uygulama alanları olduğu Dixon–Ginsparg–Harvey tarafından 1988 yılında öne sürüldü(Dixon, Ginsparg & Harvey (1989)). HS. Onlar, vektör uzaylarını V(g) konformal alan teorisinin moonshine simetrisiyle bükülmüş sektörleri olarak ve f(g,h,τ) fonksiyonunu da simitin bir formu olan ve bükülmüş sınır koşullarıyla birleştirilmiş genus ve bölme fonksiyonu olarak yorumladılar. Matematik dilinde, bükülmüş sektörler indirgenemez bükülmüş modüllerdir. Ayrıca, bölüm fonksiyonları eliptik eğriler temel monster demetleri için tasarlanmıştır.
Kuantum kütleçekiminin konjektür ilişkisi
2007 yılında, Edward Witten, AdS/CFT birebir eşlemesinin ikililiğe yol açtığını önesürdü, (2+1)-boyutlu Anti-de Sitter uzayıdaki saf kuantum kütleçekimi ile uç holomorf CFT'ler arasında. (2+1) boyuttaki saf yer çekiminin hiçbir yerel serbestlik derecesi olmamasına rağmen, kozmolojik sabit negatifken, BTZ karadelik çözümlerinin varlığından dolayı, teoride bir sabit olmayan içerik oluşuyor. Uç CFT'ler, G. Höhn tarafından üretilen, düşük enerjideki Virasoro birincil alanlarının azlığı ile ayırt ediliyorlar ve moonshine modülü sadece bir örnek.
Witten'nın varsayımı altında (Witten (2007)) mümkün olabilecek en büyük kozmolojik basit ile AdS'deki kütleçekimi, AdS/CTF ikili holomofik CFT'dir, merkezi yükü c=24'ken ve CFT'nın bölüm fonksiyonu tam olarak j-744'tür, mesela, moonshine modülünün derecelendirilmiş karakteri. Frenkel-Lepowsky-Meurman varsayımı kabul edilerek, Moonshine modülü biricik holomorfik VOA ile 24 merkezi yükü ve j-744 karakteri vardır. the Monster CFT'nın, mümkün olabilecek en büyük negatif kozmolojik sabit ile olan saf kütleçekimine, benzer olduğu sonucuna vardır, Edward Witten. Witten'nin önerisinin bir kısmı derki, Virasoro birincil alanları, karadelik oluşturan operatörlere eşittir, ve, uygunluğunu ölçekmek için, büyük-kütle limitinde, Bekenstein-Hawking kısmen-klasik entropisi, moonshine modülünde Virasoro'un birincil çarpan eşinin logaritması ile verilmiş olan kara delik kütlesinin uyumlu olduğunu buldu. Az-kütle üstünlüğü varken, bir kuantum düzeltmesi gerekti entropiye. En düşük enerji birinclik alanı log(196883) ~ 12.19'ı gösterirken, Beckenstein–Hawking tahmini hesabı 4π ~ 12.57'ı gösterdi.
Mathieu Moonshine
2010 yılında, Tohru Eguchi, Hirosi Ooguri ve Yuji Tachikawa, K3 yüzeyinin eliptik kısımının, N=(4.4)'nın karakterlerine parçalanabileceğini gösterdi. Öyle ki, süper Virasoro cebirinin çeşitliliğinin, Mathieu grup M24'nın indirgenemez temsillerinin basit kombinasyonları olduğu ortaya çıktı. Bu gösterdi ki, Sigma modelinin K3 hedefiyle konformal alan teorisinin M24 simetrisini taşıdığını gösterdi. Buna rağmen, Mukai-Kondo sınıflandırmasıyla, herhangi bir K3 yüzeyinde simplektik otomorfizmalar tarafından, bu grubun hiçbir sadaketli eyleminin olmadığını görüldü. Gaberdiel–Hohenegger–Volpato'nın çalışmalarıyla, herhangi bir K3 sigma-model konformal alan teorsinde sadakatli eylemin olmadığı da görüldü. Bu yüzden, Hilbert uzayının temelinde olan bir eylemin dış görünüşünü hala açıklanamadı.
Daha önce bahsedilen McKay–Thompson serileriyle analoji yaparak, Cheng, hem çokluk fonksiyonlarının hem de M24'ün basit olmayan elemanlarının sınıflandırılmış izleri, sahte modüler formunu biçimlendireceğini, öne sürdü. 2012 yılında, Gannon, tüm,ama ilk hariç, çeşitliliklerin, M24'ün temsillerinin negatif olmayan integral kombinasyonları olduğunu ispatladı ve Gaberdiel–Persson–Ronellenfitsch–Volpato, genelleştirilmiş moonshine fonksiyonlarının tüm analojileri hesapladılar ve Mathie moonshine'na dayandığını öne sürdüler, konformal alan teorisinin bazı analojilerinin.
Neden "monstrous moonshine"?
Monstrous moonshine terimi Conway tarafından icat edilmiştir. Conway'e, John Mckay 1970ların sonlarında, 
Monster grupları, Jean-Pierre Serre, Andrew Ogg and John G. Thompson adlı matematikçiler tarafından 1970'lerde incelenmiştir. Hiperbolik yüzeyin bölüm gruplarını SL2(R)'nın altgruplarıyla çalışmışlardır, özellikle, normalleştiren (p)'nın Γ0(p)'sını SL(2,R)'da incelemişlerdir.
Notlar
- ^ Roberts, Siobhan (2009), King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry (İngilizce), Bloomsbury Publishing USA, s. 361, ISBN , 6 Ağustos 2020 tarihinde kaynağından , erişim tarihi: 21 Aralık 2014.
- ^ Conway, J. and Norton, S. "Monstrous Moonshine", Table 2a, p.330, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.103.3704&rep=rep1&type=pdf 19 Mart 2016 tarihinde Wayback Machine sitesinde .
- ^ . 21 Aralık 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Aralık 2014.
Kaynakça
- John Horton Conway and , Monstrous Moonshine, Bull. London Math. Soc. 11, 308–339, 1979. DOI:10.1112/blms/11.3.308 10.1112/blms/11.3.308
- Frenkel, I.; Lepowsky, J.; Meurman, A. (1988), "Vertex Operator Algebras and the Monster", Pure and Applied Math., Academic Press, cilt 134
- Borcherds, Richard (1992), "Monstrous Moonshine and Monstrous Lie Superalgebras", Invent. Math., cilt 109, ss. 405-444, doi:10.1007/bf01232032, 1 Eylül 2014 tarihinde kaynağından , erişim tarihi: 21 Aralık 2014
- Terry Gannon, Monstrous Moonshine: The first twenty-five years, 2004, online
- Terry Gannon, Monstrous Moonshine and the Classification of Conformal Field Theories, reprinted in Conformal Field Theory, New Non-Perturbative Methods in String and Field Theory, (2000) Yavuz Nutku, Cihan Saclioglu, Teoman Turgut, eds. Perseus Publishing, Cambridge Mass. (Provides introductory reviews to applications in physics).
- Gannon, Terry (2006), Moonshine beyond the Monster: The Bridge Connecting Algebra, Modular Forms and Physics, ISBN
- Dixon, L.; Ginsparg, P.; Harvey, J. (1989), "Beauty and the Beast: superconformal symmetry in a Monster module", Comm. Math. Phys., cilt 119, ss. 221-241, doi:10.1007/bf01217740
- Witten, Edward (22 Haziran 2007), Three-Dimensional Gravity Revisited (PDF), 17 Temmuz 2017 tarihinde kaynağından (PDF), erişim tarihi: 21 Aralık 2014
- Maloney, Alexander; Witten, Edward (2 Aralık 2007), Quantum Gravity Partition Functions In Three Dimensions (PDF), 7 Şubat 2019 tarihinde kaynağından (PDF), erişim tarihi: 21 Aralık 2014
- Li, Wei; Song, Wei; Strominger, Andrew (21 Temmuz 2008), CHIRAL GRAVITY IN THREE DIMENSIONS (PDF), 7 Şubat 2019 tarihinde kaynağından (PDF), erişim tarihi: 21 Aralık 2014
- Duncan, John F. R.; Frenkel, Igor B. (12 Nisan 2012), Rademacher sums, moonshine and gravity (PDF), 7 Şubat 2019 tarihinde kaynağından (PDF), erişim tarihi: 21 Aralık 2014
- Maloney, Alexander; Song, Wei; Strominger, Andrew (2010), "Chiral gravity, log gravity, and extremal CFT" (PDF), Phys. Rev. D, cilt 81, doi:10.1103/physrevd.81.064007, 7 Şubat 2019 tarihinde kaynağından (PDF), erişim tarihi: 21 Aralık 2014
- Koichiro Harada, Monster, Iwanami Pub. (1999) , (The first book about the Monster Group written in Japanese).
- , Symmetry and the Monster, Oxford University Press, 2006. (Concise introduction for the lay reader).
- , Finding Moonshine, A Mathematician's Journey Through Symmetry. Fourth Estate, 2008 ,
- (1974), (PDF), Seminaire Delange-Pisot-Poitou. Theorie des nombres, tome 16, no. 1 (1974–1975), exp. no. 7, 6 Aralık 2013 tarihinde kaynağından (PDF) arşivlendi, erişim tarihi: 21 Aralık 2014
Dış bağlantılar
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte monstrous moonshine ve moonshine teorisi terimleri John Horton Conway ve Simon P Norton tarafindan dusunulmustur Zamaninda monster grup ve moduler fonksiyonlar arasindaki beklenmedik bagintiyi tanimlamak icin kullanilmistir Su an biliniyor ki monstrous moonshine nin altinda yatan simetriler gibi monster grup iceren conformal field teorisidir Varsayimlar Conway ve Norton tarafindan yapildi ve 1992 yilinda ispatida Richard Borcherds tarafindan string teori vertex operator cebiri teorisi ve genisletilmis Kac Moody cebirinden no ghost teoremini kullanilarak yapilmistir Tarihi1978 yilinda John McKay nin Fourier aciliminin ilk birkac terimin j t 1q 744 196884q 21493760q2 864299970q3 20245856256q4 displaystyle j tau frac 1 q 744 196884 q 21493760 q 2 864299970 q 3 20245856256 q 4 cdots q e2pit displaystyle q e 2 pi i tau ve t yarim zaman orani ile birlikte master gruplarin indirgenemez temsilcilerinin boyutunun lineer kombinasyonu olarak ifade edilebilir Eger rn displaystyle r n 1 196883 21296876 842609326 18538750076 19360062527 293553734298 ise 1 r1196884 r1 r221493760 r1 r2 r3864299970 2r1 2r2 r3 r420245856256 3r1 3r2 r3 2r4 r5333202640600 5r1 5r2 2r3 3r4 2r5 r7 displaystyle begin aligned 1 amp r 1 196884 amp r 1 r 2 21493760 amp r 1 r 2 r 3 864299970 amp 2r 1 2r 2 r 3 r 4 20245856256 amp 3r 1 3r 2 r 3 2r 4 r 5 333202640600 amp 5r 1 5r 2 2r 3 3r 4 2r 5 r 7 end aligned rn arasinda birden cok lineer baginti olabileceginden ornek olarak r1 r3 r4 r5 r6 0 displaystyle r 1 r 3 r 4 r 5 r 6 0 birden cok sekilde tasvir edilebilinir McKay bunu dogal olarak meydana gelen bir sonsuz boyutlu M nin kademeli gosterimi olan Hilbert Poincare serisinin j katsayisiyla verilmis ve dusuk agirlikli parcalarin yukarida oldugu gibi indirgenmez gosteriminin icinde curumesinin kaniti olarak gordu John G Thompson ina bu durumdan bahsettikten sonra Thompson Hilbert Poincare serisinin sadece birim elemanin kademeli ilkkosegen toplami olabilecegini one surdu Ve cozulmesi kolay olmanyan M nin g sinin kademeli ilkkosegen toplaminin enteresan olabilecegini one surdu Conway and Norton bu tarz kademeli ilkkosegen toplamlarini hesaplamislardi simdi McKay Thompson Tg serileri olarak bilinen yapilari ve hepsinin Hauptmoduln nin acilimlari oldugunu bulmuslardi Bir baska deyisle eger Gg nin bir altkumesiyse ki bu Tyi duzeltir o zaman karisik duzlemin upper half inin quotient asiGicin bir kuredir sonlu sayida sayinin silinmesiyle ve buna ek olarakT Meromorf fonksiyonunun cismini uretir bu kure uzerinde Olcumlerine dayanak Conway ve Norton bir Hauptmoduln listesi olusturdu ve olabilecegi Mnin kademeli sunumunun sonsuz boyutlulugunun mevcudiyetinin olabilecegi ongorusunde bulundular Bunun kademeli ilkkosegen toplamlari Tg tam olarak yaptiklari listedeki fonksiyonlarin acilimlariydi 1980 yilinda A Oliver L Atkin Paul Fong ve Stephen D Smith boyle kademeli gosterimimlerinin mumkun olabilecegini gosterdi bilgisayar hesap makineleri kullanarak bir sinira kadar j katsayilarinin m gosterimi Thompson tarafindan zaten ispatlanmisti kademeli gosterimi bariz bir sekilde Igor Frenkel James Lepowsky and Arne Meurman tarafindan etkileyici bir cozum verilerek McKay Thompson varsayimina insa edilmistir Buna ek olarak onlarin insa ettigi vektor uzayi Moonshine Module diye adlandirilan vertex operator cebirinin fazldan bir yapisi vardir Ve bu yapinin automorphism grubu tam olarak M idi Borcherds Conway Norton varsayimini 1992 yilinda kanitladi Moonshine Module icin Fields madalyasini kazandi 1998 yilinda varsayimi cozdugu kisim icin The Monster moduluFrenkel Lepowsky Meurman yapisinin iki temel arac kullanir Lattice vertex operator cebiri yapisi VL n rankin lattice L icin olsa bile Fiziksel anlamda icin simit sekli ustunde VL lattice vertex operatoru chiral cebiridir Bosonic string kompaktlastirilmasiyla n boyuttaki Osilator gosterimiyle hemen hemen tanimlanabilir L nin group ring nin tensor product i olarak ki bu demektir ki sonsuz coklukta jenerator durumu icin polynomial ring isomorphictir Sorudaki durum icin L kumesinin Leech lattice olacak sekilde ayarlanmasi gerekir 24 ranki olan Ikinci arac orbifold yapisi diye adlandirilir Fiziksel anlamda orbifold un temsil ettigi bosonic string salinimlaridir quotient orbifold ustunde Frenkel Lepowsky Meurman yapisi conformal field teoride ilk ortaya cikan orbifoldlardir Leech lattice nin tersine fonksiyonel olarak bagimli olan VL nin h sidir Moonshine modulunu elde etmek icin h nin sabit bir noktasi secilir V nin direkt toplamlarinda ve onun twisted modulunu alir Frenkel Lepowsky ve Meurman gosterdi ki moonshine modulunun automorphism gruplari vertex operator cebir olanlari M dir ve kademeli boyut j nin bir Fourier serisi acilimi verir Frenkel Lepowsky amp Meurman 1988 Borcherds in ispatiConway and Norton nin ongorusune olan Richard Borcherds nin ispati 6 parcada anlatilabilinir Otomorfizmler kullanarak M e yapilan bir hamle ve kademeli boyutlu j ile Vertex operator cebiri olan V i secerek baslanir Moonshine Module tarafindan saglanmistir ayrica monster vertex cebiri diye de adlandirilir Lie cebiri m displaystyle mathfrak m monster Lie cebiri diye adlandirilan kuantalama fonktoru kullanilarak yapilandirilmistir Bu genellestirilmis Kac Moody cebiridir otomorfizm i kullanarak Monster hamlesinden Genellestirilmis Kac Moody Lie cebirini olusturmak icin Koike Norton Zagier sonsuz carpim ozdesligi kullanilir Ozdeslik Hecke operetoru kullanarak saglanmistir Kok cesitliligi karsilastirilarak Lie cebirlerinin izomorf oldugu bulunabilinir Benzer yolla Weyl bolen formulu m displaystyle mathfrak m icin tam olarak Koike Norton Zagier ozdesligine denktir kullanarak ve Adams operatorlerini twisted bolun ozdesligi her eleman icin verilir Bu ozdeslikler McKay Thompson serileriyle baglantilidirlar Koike Norton Zagier ozdeslikleriyle baglantili olduklari gibi Twisted bolen ozdesligi yineleme iliskilerini ima eder Tg nin katsayilari ustunde Bu iliskiler o kadar gucludur ki sadece Conway and Norton tarafindan verilen bir fonksiyonla ilk yedi terimin saglanmasi yeter Boylelikle ispat tamamlanmistir Borcherds 1992 Borcherds sonralari bu ispati su sozleriyle anmistir Ben Ay in otesindeydim moonshine sanisini ispatliyorken Ve bazen merak ediyorum eger belirli ilaclar alindiginda hissedilen ben ispatlarken hissettiklerimse ama gercekten bilmiyorum cunku daha o teorimi test etmedim Genellestirilmis MoonshineConway ve Norton 1979 yilinda yazdiklari makalede moonshine nin monster ile sinirli olmayabilecegini belirttiler ama bu fenomen baska gruplar icin bulunabilinir T1A ve M T2A ve F2 T2B ve T3A ve Fi23 Fi24 T3C ve Th F3 T4A ve T4A ve McL T5A ve HN F5 T6A ve Fi22 T6B ve Suz T7A ve He F7 T10A ve HS 1980 yilinda Sporadic gruplarinin boyutlarinin basit kombinaslonlari kullanilarak bircok McKay Thompson Hauptmodul serisinin acilabilecek sekilde insa edilebilecegini buldu Larissa Queen ve digerleri Genellestirilmis Moonshine sanisini formule etmek icin Norton kendi hesaplamalarini Queen ninkilerle karsilastirdi 1987 yilinda Monster in her g elemani kademeli vektor uzayi V g ve upper half duzleminde Holomorf fonksiyonunun f g h t her g h elemanini degistiren icin asagidaki sartlarin saglanabilecegini one surer bu sani Her V g g nin merkezleyicisinin kademeli izdusumsel gosterimidir Her f g h t ya sabit bir fonksiyon veyahut Hauptmodul dur Her f g h t M de g ve h nin eszamanli konjugasyonun altinda sabit niceligidir Her g h icin V g ustunde bir dogrusal donusum vardir Herhangi bir abcd SL2 Z displaystyle begin pmatrix a amp b c amp d end pmatrix in SL 2 mathbf Z icin f g h at bct d displaystyle f g h frac a tau b c tau d f gahc gbhd t displaystyle f g a h c g b h d tau ye dogru orantilidir Eger g h 1 ise f g h t j ye dogru orantilidir Bu Conway Norton sanisinin genelestirilmis halidir cunku Borcherds nin teoremi eger g bir birim kumesi oldugu durumla ilgililenir Su an hala bu sanasi hala sadece bir sanidir Conway Norton sanisinda oldugu gibi Genellestirilmis Moonshine ninda fizikte uygulama alanlari oldugu Dixon Ginsparg Harvey tarafindan 1988 yilinda one suruldu Dixon Ginsparg amp Harvey 1989 HS Onlar vektor uzaylarini V g konformal alan teorisinin moonshine simetrisiyle bukulmus sektorleri olarak ve f g h t fonksiyonunu da simitin bir formu olan ve bukulmus sinir kosullariyla birlestirilmis genus ve bolme fonksiyonu olarak yorumladilar Matematik dilinde bukulmus sektorler indirgenemez bukulmus modullerdir Ayrica bolum fonksiyonlari eliptik egriler temel monster demetleri icin tasarlanmistir Kuantum kutlecekiminin konjektur iliskisi2007 yilinda Edward Witten AdS CFT birebir eslemesinin ikililige yol actigini onesurdu 2 1 boyutlu Anti de Sitter uzayidaki saf kuantum kutlecekimi ile uc holomorf CFT ler arasinda 2 1 boyuttaki saf yer cekiminin hicbir yerel serbestlik derecesi olmamasina ragmen kozmolojik sabit negatifken BTZ karadelik cozumlerinin varligindan dolayi teoride bir sabit olmayan icerik olusuyor Uc CFT ler G Hohn tarafindan uretilen dusuk enerjideki Virasoro birincil alanlarinin azligi ile ayirt ediliyorlar ve moonshine modulu sadece bir ornek Witten nin varsayimi altinda Witten 2007 mumkun olabilecek en buyuk kozmolojik basit ile AdS deki kutlecekimi AdS CTF ikili holomofik CFT dir merkezi yuku c 24 ken ve CFT nin bolum fonksiyonu tam olarak j 744 tur mesela moonshine modulunun derecelendirilmis karakteri Frenkel Lepowsky Meurman varsayimi kabul edilerek Moonshine modulu biricik holomorfik VOA ile 24 merkezi yuku ve j 744 karakteri vardir the Monster CFT nin mumkun olabilecek en buyuk negatif kozmolojik sabit ile olan saf kutlecekimine benzer oldugu sonucuna vardir Edward Witten Witten nin onerisinin bir kismi derki Virasoro birincil alanlari karadelik olusturan operatorlere esittir ve uygunlugunu olcekmek icin buyuk kutle limitinde Bekenstein Hawking kismen klasik entropisi moonshine modulunde Virasoro un birincil carpan esinin logaritmasi ile verilmis olan kara delik kutlesinin uyumlu oldugunu buldu Az kutle ustunlugu varken bir kuantum duzeltmesi gerekti entropiye En dusuk enerji birinclik alani log 196883 12 19 i gosterirken Beckenstein Hawking tahmini hesabi 4p 12 57 i gosterdi Mathieu Moonshine2010 yilinda Tohru Eguchi Hirosi Ooguri ve Yuji Tachikawa K3 yuzeyinin eliptik kisiminin N 4 4 nin karakterlerine parcalanabilecegini gosterdi Oyle ki super Virasoro cebirinin cesitliliginin Mathieu grup M24 nin indirgenemez temsillerinin basit kombinasyonlari oldugu ortaya cikti Bu gosterdi ki Sigma modelinin K3 hedefiyle konformal alan teorisinin M24 simetrisini tasidigini gosterdi Buna ragmen Mukai Kondo siniflandirmasiyla herhangi bir K3 yuzeyinde simplektik otomorfizmalar tarafindan bu grubun hicbir sadaketli eyleminin olmadigini goruldu Gaberdiel Hohenegger Volpato nin calismalariyla herhangi bir K3 sigma model konformal alan teorsinde sadakatli eylemin olmadigi da goruldu Bu yuzden Hilbert uzayinin temelinde olan bir eylemin dis gorunusunu hala aciklanamadi Daha once bahsedilen McKay Thompson serileriyle analoji yaparak Cheng hem cokluk fonksiyonlarinin hem de M24 un basit olmayan elemanlarinin siniflandirilmis izleri sahte moduler formunu bicimlendirecegini one surdu 2012 yilinda Gannon tum ama ilk haric cesitliliklerin M24 un temsillerinin negatif olmayan integral kombinasyonlari oldugunu ispatladi ve Gaberdiel Persson Ronellenfitsch Volpato genellestirilmis moonshine fonksiyonlarinin tum analojileri hesapladilar ve Mathie moonshine na dayandigini one surduler konformal alan teorisinin bazi analojilerinin Neden monstrous moonshine Monstrous moonshine terimi Conway tarafindan icat edilmistir Conway e John Mckay 1970larin sonlarinda q displaystyle q nin 196884 olarak adlandirilan tam olarak Griess cebirinin boyutu oldugu soylendiginde Conway bunun moonshine oldugunu soylemistir delice ve aptalca bir fikir olmasi acisindan Boylelikle bu terim sadece Monster gruplardan bashetmiyor ayrica moduler fonksiyonlar teorisineden bahsetmis oluyor Monster gruplari Jean Pierre Serre Andrew Ogg and John G Thompson adli matematikciler tarafindan 1970 lerde incelenmistir Hiperbolik yuzeyin bolum gruplarini SL2 R nin altgruplariyla calismislardir ozellikle normallestiren p nin G0 p sini SL 2 R da incelemislerdir Notlar Roberts Siobhan 2009 King of Infinite Space Donald Coxeter the Man Who Saved Geometry Ingilizce Bloomsbury Publishing USA s 361 ISBN 9780802718327 6 Agustos 2020 tarihinde kaynagindan erisim tarihi 21 Aralik 2014 Conway J and Norton S Monstrous Moonshine Table 2a p 330 http citeseerx ist psu edu viewdoc download doi 10 1 1 103 3704 amp rep rep1 amp type pdf 19 Mart 2016 tarihinde Wayback Machine sitesinde 21 Aralik 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Aralik 2014 KaynakcaJohn Horton Conway and Monstrous Moonshine Bull London Math Soc 11 308 339 1979 DOI 10 1112 blms 11 3 308 10 1112 blms 11 3 308 Frenkel I Lepowsky J Meurman A 1988 Vertex Operator Algebras and the Monster Pure and Applied Math Academic Press cilt 134 Borcherds Richard 1992 Monstrous Moonshine and Monstrous Lie Superalgebras Invent Math cilt 109 ss 405 444 doi 10 1007 bf01232032 1 Eylul 2014 tarihinde kaynagindan erisim tarihi 21 Aralik 2014 Terry Gannon Monstrous Moonshine The first twenty five years 2004 online Terry Gannon Monstrous Moonshine and the Classification of Conformal Field Theories reprinted in Conformal Field Theory New Non Perturbative Methods in String and Field Theory 2000 Yavuz Nutku Cihan Saclioglu Teoman Turgut eds Perseus Publishing Cambridge Mass ISBN 0 7382 0204 5 Provides introductory reviews to applications in physics Gannon Terry 2006 Moonshine beyond the Monster The Bridge Connecting Algebra Modular Forms and Physics ISBN 0 521 83531 3 Dixon L Ginsparg P Harvey J 1989 Beauty and the Beast superconformal symmetry in a Monster module Comm Math Phys cilt 119 ss 221 241 doi 10 1007 bf01217740 Witten Edward 22 Haziran 2007 Three Dimensional Gravity Revisited PDF 17 Temmuz 2017 tarihinde kaynagindan PDF erisim tarihi 21 Aralik 2014 Maloney Alexander Witten Edward 2 Aralik 2007 Quantum Gravity Partition Functions In Three Dimensions PDF 7 Subat 2019 tarihinde kaynagindan PDF erisim tarihi 21 Aralik 2014 Li Wei Song Wei Strominger Andrew 21 Temmuz 2008 CHIRAL GRAVITY IN THREE DIMENSIONS PDF 7 Subat 2019 tarihinde kaynagindan PDF erisim tarihi 21 Aralik 2014 Duncan John F R Frenkel Igor B 12 Nisan 2012 Rademacher sums moonshine and gravity PDF 7 Subat 2019 tarihinde kaynagindan PDF erisim tarihi 21 Aralik 2014 Maloney Alexander Song Wei Strominger Andrew 2010 Chiral gravity log gravity and extremal CFT PDF Phys Rev D cilt 81 doi 10 1103 physrevd 81 064007 7 Subat 2019 tarihinde kaynagindan PDF erisim tarihi 21 Aralik 2014 Koichiro Harada Monster Iwanami Pub 1999 ISBN 4 00 006055 4 The first book about the Monster Group written in Japanese Symmetry and the Monster Oxford University Press 2006 ISBN 978 0 19 280723 6 Concise introduction for the lay reader Finding Moonshine A Mathematician s Journey Through Symmetry Fourth Estate 2008 ISBN 0 00 721461 8 ISBN 978 0 00 721461 7 1974 PDF Seminaire Delange Pisot Poitou Theorie des nombres tome 16 no 1 1974 1975 exp no 7 6 Aralik 2013 tarihinde kaynagindan PDF arsivlendi erisim tarihi 21 Aralik 2014 Dis baglantilar Wayback Machine
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State