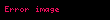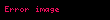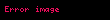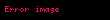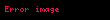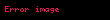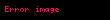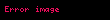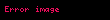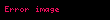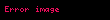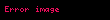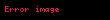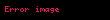Ohm yasası, bir elektrik devresinde iki nokta arasındaki iletken üzerinden geçen akım, potansiyel farkla (örn. voltaj veya gerilim düşümü) doğru; iki nokta arasındaki dirençle ters orantılıdır.

ya da
Burada, I akım amper, V referans alınan iki nokta arasındaki potansiyel fark volt ve R ohmla ölçülen ve direnç olarak adlandırılan devre değişkeni (volt/amper)dir. Potansiyel fark gerilim olarak da bilinir ve bazen V nin yerine U, E veya emk (elektromotor kuvvet) sembolleri kullanılır.
Bu yasa basit elektriksel devrelerdeki telden geçen akım ve gerilim miktarını açıklar.
Yukarıdaki formül elektrik/elektronik mühendisliği alanında oldukça sık kullanılan bir eşitliktir. Çünkü gerilim, akım ve direncin birbirleriyle olan ilişkisini makroskopik seviyede inceler. Bu elemanlar çoğunlukla bir elektrik devresinde bulunur.
Basit tanımlama ve kullanımı
Elektriksel aygıtları içeren elektrik devreleri birbirlerine iletkenlerle bağlanır. Yukarıdaki diyagram yapılabilen en basit elektrik devrelerinden biridir. Batarya gibi bir elektriksel aygıt içinde + ve - terminalleri bulunan bir çemberle gösterilir. Diğer aygıt zikzak şeklinde resmedilir ve arkasına R harfi konur ve direnç olarak adlandırılır. Gerilim kaynağının + veya pozitif ucu direnci önemsenmeyen bir iletkenle direnç uçlarının birine bağlanmıştır. Bu iletkenden geçen akım I ve ok işareti akımın yönünü gösterir. Direncin ikinci ucu başka bir iletkenle voltaj kaynağının - ucuna bağlanır. Bu form kapalı devredir. Çünkü gerilim kaynağının bir ucundan çıkan akım diğer ucuna dönmüştür.
Gerilim negatif yüklü elektronların iletken boyunca hareket ettiği bir elektriksel kuvvettir. Akım elektron akışına ters yönde akar ve direnç akıma karşı gösterilen zorluktur.
Ohm yasasında bahsedilen 'iletken' üzerinde gerilimin ölçüldüğü bir devre elemanıdır. Dirençler elektrik şarjının üzerinden yavaşça aktığı iletkenlerdir. 10 megaohmluk bir dirence sahip olan bir iletken 0,1 ohmluk bir dirence sahip olan iletkene göre daha zayıf bir iletkendir ve iyi iletken sayılmaz. (Yalıtkan maddelere bir gerilim uygulandığında akımın geçmesine izin vermezler.)
Fizik
Fizikçiler Ohm yasasının şu formunu sık kullanır:
Burada J akım yoğunluğu, (akım/birim alan, Ohm yasasındaki I akımına benzemez), σ (anisotropik maddelerde Tensör olabilir) ve E elektrik alanı (volt/metre, Ohm yasasındaki V birimine benzemez) dır. Yukarıdaki ifade üç boyutlu her bir vektörün kullanılan biçimlerden biri değildir. (Normalde aşağıdaki örnekte görüleceği şekildedir. Bazen noktanın anlamı skaler çarpımdır. Buradaki nokta sadece basitce kullandığımız matematiksel çarpım anlamındadır.) Buradaki J de görüldüğü gibi kullanılan kartezyen koordinatları, vektördeki her bir bileşen için üç farklı bileşen vardır, Her bileşeninde üç farklı değeri vardır. Örneğin, J ögesinin x, y ve z yönlerinde Jx(x,y,z), Jy(x, y, z) ve Jz(x, y, z) gibi bileşenleri vardır.
Devre tasarımında kullanılan form makroskopiktir, Ohm'un genel formu yaklaşık olarak şu şekilde elde edilir:
Belirlenen iki nokta arasındaki potansiyel fark;
veya elektriksel alan bağımsız yoldadır, 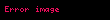
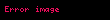
e İletkenin elektrik direnci öziletkenlik, uzunluk ve kesit alanı ile ifade edilir:
Eğer madde B manyetik alannında v hızıyla hareket ediyorsa forma şu ifadeye şu eklenmelidir
Mükemmel metal kafeste yoktur, fakat gerçek bir metalde , kirlilikler, çoklu izotoplar ve atomların ısısal hareketler gibi etkiler vardır. Bunlar elektronların saçılmasına sebep olarak dirençte değişiklik oluştururlar.
Ohm yasası Kirçoh gerilim yasası (KVL) ve Kirşof akım yasası (KCL) nu elde etmek için yeterlidir. İlk eşitliğin sadece sağ tarafına bakarsak:
ve kapalı integral uygularsak:
Yüzey boyunca Stokes teoremini yazabiliriz:
fakat E potansiyeli yönsüz olarak kabul edeceğiz:
her iki tarafa yine kapalı integrali uygularsak:
Maxwell denklemlerinden 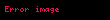
daha önceki eşitliklerden sağ tarafın sıfır olduğunu biliyoruz:
bu açık yüzeydeki net akımın sıfır olduğunu gösteriyor.
Elektrik ve elektronik mühendisliğinde kullanımı
Ohm yasası elektrik devrelerinin analizinde kullanılan bir eşitliktir, mühendisler ve bilgisayarcılar tarafından da kullanılır. bugün bile iş yoğunluğunu azaltmak için elektrik devrelerin analizinde bilgisayarlarda kullanılıyor.
Hemen hemen bütün devrelerde dirençli elemanlar vardır ki bunların hemen hemen hepsinde ideal omik devreler dikkate alınır.
Hidrolik analog
Gerilim, akım ve direnç değerleri soyut kavramlardır,Başlangıçta elektrik mühendisliği öğrencileri su akışı için yardımcı analog terimler buldular. Su basıncı, pascal ile ölçülür ve, analog gerilimdir. Çünkü su akışını (yatay) olarak sağlayan borunun iki nokta arasındaki su basınç farkı hesaplanıyor Suyun akışı litre (veya galon) dakikadaki su miktarıdır. coulomb/saniye gibi analog bir akımdır.
Şerit direnci
Genellikle yalıtılmış tabakalara yerleştirilen ince metal şeritler elektrik akımını filmin yüzeyine paralel olarak taşınmak için kullanılır. Çoğu aygıtın elektriksel hassasiyetini açıklamak için ohm/birim kare terimi kullanılır.
Sıcaklık etkileri
İletkenin sıcaklığı yükseldiğinde elektron ve atomlar arasındaki çarpışmalar da artar. Bu bir maddeyi ısıtmak gibidir Elektriksel akış artacağından dolayı direnç de artacak. Yarı iletkenler istisnadır. Ohmik bir maddenin direnci sıcaklığa bağlıdır. Bu sıcaklıktan bağımsızlık ohmik olmayan maddeler için geçerli değildir, çünkü verilen sıcaklıkta, akım ve gerilimle değişmez.
AC devreler
Bir AC devresi içim Ohm yasası şöyle yazılabilir 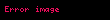
,
Burada d yük empedansından farklıdır 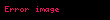
Kaynakça
Dış bağlantılar
| Wikimedia Commons'ta Ohm kanunu ile ilgili ortam dosyaları bulunmaktadır. |
- John C. Shedd and Mayo D. Hershey,"The History of Ohm's Law" 28 Mayıs 2013 tarihinde Wayback Machine sitesinde ., Popular Science, December 1913, pages 599-614, Bonnier Corporation ISSN 0161-7370, gives the history of Ohm's investigations, prior work, Ohm's false equation in the first paper, illustration of Ohm's experimental apparatus.
- Morton L. Schagrin, "Resistance to Ohm's Law", American Journal of Physics, July 1963, Volume 31, Issue 7, pp. 536–47. Explores the conceptual change underlying Ohm's experimental work.
- Kenneth L. Caneva, "Ohm, Georg Simon." 8 Mart 2012 tarihinde Wayback Machine sitesinde . . 2008
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Ohm yasasi bir elektrik devresinde iki nokta arasindaki iletken uzerinden gecen akim potansiyel farkla orn voltaj veya gerilim dusumu dogru iki nokta arasindaki direncle ters orantilidir source source source source source source source source Bir gerilim kaynagi V ndan cikan elektrik akimi I direnc R uzerinden gecer Bu su sekildedir Ohm yasasi V IR I VR displaystyle I dfrac V R ya da V I R displaystyle V I R Burada I akim amper V referans alinan iki nokta arasindaki potansiyel fark volt ve R ohmla olculen ve direnc olarak adlandirilan devre degiskeni volt amper dir Potansiyel fark gerilim olarak da bilinir ve bazen V nin yerine U E veya emk elektromotor kuvvet sembolleri kullanilir Bu yasa basit elektriksel devrelerdeki telden gecen akim ve gerilim miktarini aciklar Yukaridaki formul elektrik elektronik muhendisligi alaninda oldukca sik kullanilan bir esitliktir Cunku gerilim akim ve direncin birbirleriyle olan iliskisini makroskopik seviyede inceler Bu elemanlar cogunlukla bir elektrik devresinde bulunur Basit tanimlama ve kullanimiElektriksel aygitlari iceren elektrik devreleri birbirlerine iletkenlerle baglanir Yukaridaki diyagram yapilabilen en basit elektrik devrelerinden biridir Batarya gibi bir elektriksel aygit icinde ve terminalleri bulunan bir cemberle gosterilir Diger aygit zikzak seklinde resmedilir ve arkasina R harfi konur ve direnc olarak adlandirilir Gerilim kaynaginin veya pozitif ucu direnci onemsenmeyen bir iletkenle direnc uclarinin birine baglanmistir Bu iletkenden gecen akim I ve ok isareti akimin yonunu gosterir Direncin ikinci ucu baska bir iletkenle voltaj kaynaginin ucuna baglanir Bu form kapali devredir Cunku gerilim kaynaginin bir ucundan cikan akim diger ucuna donmustur Gerilim negatif yuklu elektronlarin iletken boyunca hareket ettigi bir elektriksel kuvvettir Akim elektron akisina ters yonde akar ve direnc akima karsi gosterilen zorluktur Ohm yasasinda bahsedilen iletken uzerinde gerilimin olculdugu bir devre elemanidir Direncler elektrik sarjinin uzerinden yavasca aktigi iletkenlerdir 10 megaohmluk bir dirence sahip olan bir iletken 0 1 ohmluk bir dirence sahip olan iletkene gore daha zayif bir iletkendir ve iyi iletken sayilmaz Yalitkan maddelere bir gerilim uygulandiginda akimin gecmesine izin vermezler FizikFizikciler Ohm yasasinin su formunu sik kullanir J s E displaystyle mathbf J sigma cdot mathbf E Burada J akim yogunlugu akim birim alan Ohm yasasindaki I akimina benzemez s anisotropik maddelerde Tensor olabilir ve E elektrik alani volt metre Ohm yasasindaki V birimine benzemez dir Yukaridaki ifade uc boyutlu her bir vektorun kullanilan bicimlerden biri degildir Normalde asagidaki ornekte gorulecegi sekildedir Bazen noktanin anlami skaler carpimdir Buradaki nokta sadece basitce kullandigimiz matematiksel carpim anlamindadir Buradaki J de goruldugu gibi kullanilan kartezyen koordinatlari vektordeki her bir bilesen icin uc farkli bilesen vardir Her bileseninde uc farkli degeri vardir Ornegin J ogesinin x y ve z yonlerinde Jx x y z Jy x y z ve Jz x y z gibi bilesenleri vardir Devre tasariminda kullanilan form makroskopiktir Ohm un genel formu yaklasik olarak su sekilde elde edilir Belirlenen iki nokta arasindaki potansiyel fark DV E dl displaystyle Delta V int mathbf E cdot dl veya elektriksel alan bagimsiz yoldadir DV EL displaystyle Delta V E L burada L referans noktalar arasindaki uzaklik J IA displaystyle J frac I A oldugunda Ohm yasasi soyle olur IA s DV L displaystyle I over A sigma Delta V over L e Iletkenin elektrik direnci oziletkenlik uzunluk ve kesit alani ile ifade edilir R LsA displaystyle R L over sigma A DV R I displaystyle Delta V over R I Eger madde B manyetik alanninda v hiziyla hareket ediyorsa forma su ifadeye su eklenmelidir J s E v B displaystyle mathbf J sigma cdot left mathbf E mathbf v times mathbf B right Mukemmel metal kafeste yoktur fakat gercek bir metalde kirlilikler coklu izotoplar ve atomlarin isisal hareketler gibi etkiler vardir Bunlar elektronlarin sacilmasina sebep olarak direncte degisiklik olustururlar Ohm yasasi Kircoh gerilim yasasi KVL ve Kirsof akim yasasi KCL nu elde etmek icin yeterlidir Ilk esitligin sadece sag tarafina bakarsak sE displaystyle sigma E ve kapali integral uygularsak sE dl displaystyle int sigma E cdot dl Yuzey boyunca Stokes teoremini yazabiliriz Ss E dA displaystyle int S sigma nabla times E cdot dA fakat E potansiyeli yonsuz olarak kabul edecegiz Ss ϕ dA displaystyle int S sigma nabla times left nabla phi right cdot dA Ss 0 dA displaystyle int S sigma times vec 0 cdot dA J sE displaystyle J sigma E her iki tarafa yine kapali integrali uygularsak J dl sE dl displaystyle int J cdot dl oint sigma E cdot dl Maxwell denklemlerinden curl H J displaystyle curl H J H dl sE dl displaystyle int nabla times H cdot dl int sigma E cdot dl SH dA sE dl displaystyle int S H cdot dA oint sigma E cdot dl daha onceki esitliklerden sag tarafin sifir oldugunu biliyoruz SH dA 0 displaystyle int S H cdot dA 0 bu acik yuzeydeki net akimin sifir oldugunu gosteriyor Elektrik ve elektronik muhendisliginde kullanimiOhm yasasi elektrik devrelerinin analizinde kullanilan bir esitliktir muhendisler ve bilgisayarcilar tarafindan da kullanilir bugun bile is yogunlugunu azaltmak icin elektrik devrelerin analizinde bilgisayarlarda kullaniliyor Hemen hemen butun devrelerde direncli elemanlar vardir ki bunlarin hemen hemen hepsinde ideal omik devreler dikkate alinir Hidrolik analog Gerilim akim ve direnc degerleri soyut kavramlardir Baslangicta elektrik muhendisligi ogrencileri su akisi icin yardimci analog terimler buldular Su basinci pascal ile olculur ve analog gerilimdir Cunku su akisini yatay olarak saglayan borunun iki nokta arasindaki su basinc farki hesaplaniyor Suyun akisi litre veya galon dakikadaki su miktaridir coulomb saniye gibi analog bir akimdir Serit direnci Genellikle yalitilmis tabakalara yerlestirilen ince metal seritler elektrik akimini filmin yuzeyine paralel olarak tasinmak icin kullanilir Cogu aygitin elektriksel hassasiyetini aciklamak icin ohm birim kare terimi kullanilir Sicaklik etkileriIletkenin sicakligi yukseldiginde elektron ve atomlar arasindaki carpismalar da artar Bu bir maddeyi isitmak gibidir Elektriksel akis artacagindan dolayi direnc de artacak Yari iletkenler istisnadir Ohmik bir maddenin direnci sicakliga baglidir Bu sicakliktan bagimsizlik ohmik olmayan maddeler icin gecerli degildir cunku verilen sicaklikta akim ve gerilimle degismez AC devrelerBir AC devresi icim Ohm yasasi soyle yazilabilir V I Z displaystyle mathbf V mathbf I cdot mathbf Z Burada V ve I sirasiyla gerilim ve akimin titresim faz ve Z salinim frekansinin kompleks empedansi Bir iletim hattinda yukaridaki Ohm yasasinu fazor formu yansimadan dolayi gecersizdir Kayipsiz bir iletim hattinda gerilim ve akim orani asagidaki karmasik yapidadir Z d Z0ZL jZ0tan bd Z0 jZLtan bd displaystyle Z d Z 0 frac Z L jZ 0 tan beta d Z 0 jZ L tan beta d Burada d yuk empedansindan farklidir ZL displaystyle Z L dalga boyu b hattin ve Z0 displaystyle Z 0 hattin karakteristik empedansidir Kaynakca Handbook of Chemistry and Physics Fortieth Edition p 3112 1958 Electricity Encyclopedia Britannica 1911 4 Mart 2007 tarihinde kaynagindan Dis baglantilarWikimedia Commons ta Ohm kanunu ile ilgili ortam dosyalari bulunmaktadir John C Shedd and Mayo D Hershey The History of Ohm s Law 28 Mayis 2013 tarihinde Wayback Machine sitesinde Popular Science December 1913 pages 599 614 Bonnier Corporation ISSN 0161 7370 gives the history of Ohm s investigations prior work Ohm s false equation in the first paper illustration of Ohm s experimental apparatus Morton L Schagrin Resistance to Ohm s Law American Journal of Physics July 1963 Volume 31 Issue 7 pp 536 47 Explores the conceptual change underlying Ohm s experimental work Kenneth L Caneva Ohm Georg Simon 8 Mart 2012 tarihinde Wayback Machine sitesinde 2008
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State