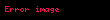Paillier şifrelemesi , 1999’da Pascal Paillier tarafından geliştirilen olasılıksal açık anahtarlı şifreleme yöntemidir. n’inci kök sınıflarını hesaplamanın zorluğunu kullanan Paillier şifreleme sistemi, kararsal bileşik kök sınıfı varsayımı (en:decisional composite residuosity assumption) üzerine kurulmuştur. Sistem, toplama işlemine göre homomorfik (homomorphic) özellik gösterir; yani sadece açık anahtarı, ve ’nin şifrelemesini kullanarak ’nin şifrelenmiş hâli hesaplanabilir.
Algoritma
Sistemin çalışma şekli aşağıda anlatılmıştır:
Anahtar Üretimi
- ”p” ve “q”, rastgele seçilen, birbirinden bağımsız ve
özelliğini sağlayan iki büyük asal sayı olsun. İki asal sayı da eşit uzunlukta seçilirse, yani güvenlik parametresi
için
ise bu koşul doğrudan sağlanır.
ve
olarak hesaplanır.
olmak üzere rastgele bir
tam sayısı seçilir. Yani g sayısı, 1 ile (n² - 1) arasında rastgele bir değer almalı ve EBOB(g, n²) = 1 özelliğini sağlamalıdır.
fonksiyonu
şeklinde tanımlanmak üzere;
’nın hesaplanabilirliği kontrol edilerek,
’nin
’nin mertebesini böldüğünden emin olunur.
gösteriminin
ile
’nin çarpmaya gore modüler tersinin çarpımına değil,
’nın b’ye bölümüne; yani
olmak üzere
eşitsizliğini sağlayan en büyük tam sayı
’ye eşit olduğuna dikkat ediniz.
- Açık Anahtar (Şifreleme Anahtarı).
- Gizli Anahtar (Şifre Çözme Anahtarı)
Eğer eşit uzunlukta p,q kullanılırsa, yukarıda anlatılan anahtar üretim işlemi, 


Şifreleme
,
koşulunu sağlayan, şifrelenecek mesaj olsun.
koşulunu sağlayan rastgele bir
seçilir. Yani r sayısı, 1 ile (n - 1) arasında rastgele bir değer almalı ve EBOB(r, n²) = 1 özelliğini sağlamalıdır.
- Şifreli metin
şeklinde hesaplanır.
Şifre Çözme
- Şifreli metin
- Mesaj
eşitliği kullanılarak hesaplanır.
Özgün makalede belirtildiği gibi şifre çözme işlemi, temel olarak, mod 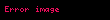
Homomorfik Özellikler
Paillier şifrelemesinin özelliği oldukça önemlidir. Şifreleme fonksiyonu toplama işlemine göre homomorfik olduğu için, aşağıdaki eşitlikler geçerlidir:
- Şifrelenmemiş metinlerin homomorfik olarak toplanması
- Şifrelenmemiş metinlerin homomorfik olarak çarpılması
- Daha genel olarak belirtmek gerekirse:
Özellikle belirtmek gerekirse, Paillier şifrelenmiş hali verilen iki mesajın çarpımının şifrelenmiş hali, gizli anahtar olmadan hesaplanamaz.
Temel Bilgiler
Paillier şifrelemesi ile, bazı ayrık logaritmaların (Ayrık logaritma) kolay bir biçimde hesaplanabileceği gösterilebilir. Örneğin, binom açılımı kullanarak,
Yukarıdaki eşitlikten
elde edilir. Buradan, eğer
ise
yazılabilir. Yani;
fonksiyonu
(tam sayı bölme işleminin bölümü) şeklinde tanımlanmak üzere ve
iken
,
yazılabilir.
Anlamsal Güvenlik
Yukarıda belirtilen orijinal kriptosistem yukarıda gösterildiği gibi seçilmiş açık metin saldırılarına karşı anlamsal güvenlik sağlar (Seçilmiş açık metin saldırısı).
Ayrıca bakınız
- Paillier’in tarihsel öncüsü Okamoto-Uchiyama şifreleme sistemi.
- Paillier’in genelleştirilmiş hâli .
- Paillier’in etkileşimli simülatörü oylama uygulamasının örneğidir.
- Paillier şifrelemesinin etkileşimli demosu
- Kriptografik yöntemler kullanılarak nasıl oylama yapılabileceğini gösteren googletechtalk videosu
Notlar
- ^ a b Jonathan Katz, Yehuda Lindell, "Introduction to Modern Cryptography: Principles and Protocols," Chapman & Hall/CRC, 2007
- ^ Pascal Paillier. (PDF). 6 Nisan 2012 tarihinde kaynağından (PDF) arşivlendi.
- ^ . 18 Şubat 2012. 18 Şubat 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Ekim 2020.
- ^ . 16 Şubat 2012. 16 Şubat 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Ekim 2020.
- ^ . 23 Aralık 2011. 23 Aralık 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Ekim 2020.
Kaynakça
- Paillier, Pascal (1999). "Public-Key Cryptosystems Based on Composite Degree Residuosity Classes". EUROCRYPT. Springer. pp. 223–238. doi:10.1007/3-540-48910-X_16
- Paillier, Pascal; Pointcheval, David (1999). "Efficient Public-Key Cryptosystems Provably Secure Against Active Adversaries". ASIACRYPT. Springer. pp. 165–179. doi:10.1007/978-3-540-48000-6_14
- Paillier, Pascal (1999). Cryptosystems Based on Composite Residuosity (Ph.D. thesis). École Nationale Supérieure des Télécommunications.
- Paillier, Pascal (2002). (PDF). CryptoBytes. 5 (1). 20 Ekim 2006 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 22 Mayıs 2012.
Dış bağlantılar
- . 29 Haziran 2012 tarihinde kaynağından arşivlendi.
Paillier şifrelemesinin homomorfik özellikleriyle beraber geliştirilmiş hâlidir
. - : Paillier şifrelemesinin ve buna dayana kriptografik sayaçların geliştirilmiş hâlini içeren açık kaynak kütüphane.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Paillier sifrelemesi 1999 da Pascal Paillier tarafindan gelistirilen olasiliksal acik anahtarli sifreleme yontemidir n inci kok siniflarini hesaplamanin zorlugunu kullanan Paillier sifreleme sistemi kararsal bilesik kok sinifi varsayimi en decisional composite residuosity assumption uzerine kurulmustur Sistem toplama islemine gore homomorfik homomorphic ozellik gosterir yani sadece acik anahtari m1 displaystyle m 1 ve m2 displaystyle m 2 nin sifrelemesini kullanarak m1 m2 displaystyle m 1 m 2 nin sifrelenmis hali hesaplanabilir AlgoritmaSistemin calisma sekli asagida anlatilmistir Anahtar Uretimi p ve q rastgele secilen birbirinden bagimsiz ve EBOB pq p 1 q 1 1 displaystyle operatorname EBOB pq p 1 q 1 1 ozelligini saglayan iki buyuk asal sayi olsun Iki asal sayi da esit uzunlukta secilirse yani guvenlik parametresi s displaystyle s icin p q 1 0 1 s 1 displaystyle p q in 1 0 1 s 1 ise bu kosul dogrudan saglanir n pq displaystyle n pq ve l EKOK p 1 q 1 displaystyle lambda operatorname EKOK p 1 q 1 olarak hesaplanir g Zn2 displaystyle g in mathbb Z n 2 olmak uzere rastgele bir g displaystyle g tam sayisi secilir Yani g sayisi 1 ile n 1 arasinda rastgele bir deger almali ve EBOB g n 1 ozelligini saglamalidir L displaystyle L fonksiyonu L u u 1n displaystyle L u frac u 1 n seklinde tanimlanmak uzere m L glmodn2 1modn displaystyle mu L g lambda mod n 2 1 mod n nin hesaplanabilirligi kontrol edilerek n displaystyle n nin g displaystyle g nin mertebesini boldugunden emin olunur ab displaystyle frac a b gosteriminin a displaystyle a ile b displaystyle b nin carpmaya gore moduler tersinin carpimina degil a displaystyle a nin b ye bolumune yani v 0 displaystyle v geq 0 olmak uzere a vb displaystyle a geq vb esitsizligini saglayan en buyuk tam sayi v displaystyle v ye esit olduguna dikkat ediniz dd n g displaystyle n g Acik Anahtar Sifreleme Anahtari l m displaystyle lambda mu Gizli Anahtar Sifre Cozme Anahtari Eger esit uzunlukta p q kullanilirsa yukarida anlatilan anahtar uretim islemi f n p 1 q 1 displaystyle varphi n p 1 q 1 olmak uzere g n 1 l f n displaystyle g n 1 lambda varphi n ve m f n 1modn displaystyle mu varphi n 1 mod n seklinde daha basit olarak yapilabilir Sifreleme m displaystyle m m Zn displaystyle m in mathbb Z n kosulunu saglayan sifrelenecek mesaj olsun r Zn displaystyle r in mathbb Z n kosulunu saglayan rastgele bir r displaystyle r secilir Yani r sayisi 1 ile n 1 arasinda rastgele bir deger almali ve EBOB r n 1 ozelligini saglamalidir Sifreli metin c gm rnmodn2 displaystyle c g m cdot r n mod n 2 seklinde hesaplanir Sifre Cozme Sifreli metin c Zn2 displaystyle c in mathbb Z n 2 Mesaj m L clmodn2 mmodn displaystyle m L c lambda mod n 2 cdot mu mod n esitligi kullanilarak hesaplanir Ozgun makalede belirtildigi gibi sifre cozme islemi temel olarak mod n2 displaystyle n 2 de yapilan bir us alma isleminden ibarettir Homomorfik Ozellikler Paillier sifrelemesinin ozelligi oldukca onemlidir Sifreleme fonksiyonu toplama islemine gore homomorfik oldugu icin asagidaki esitlikler gecerlidir Sifrelenmemis metinlerin homomorfik olarak toplanmasiD E m1 r1 E m2 r2 modn2 m1 m2modn displaystyle D E m 1 r 1 cdot E m 2 r 2 mod n 2 m 1 m 2 mod n dd D E m1 r1 gm2modn2 m1 m2modn displaystyle D E m 1 r 1 cdot g m 2 mod n 2 m 1 m 2 mod n dd Sifrelenmemis metinlerin homomorfik olarak carpilmasiD E m1 r1 m2modn2 m1m2modn displaystyle D E m 1 r 1 m 2 mod n 2 m 1 m 2 mod n D E m2 r2 m1modn2 m1m2modn displaystyle D E m 2 r 2 m 1 mod n 2 m 1 m 2 mod n dd Daha genel olarak belirtmek gerekirse D E m1 r1 kmodn2 km1modn displaystyle D E m 1 r 1 k mod n 2 km 1 mod n dd Ozellikle belirtmek gerekirse Paillier sifrelenmis hali verilen iki mesajin carpiminin sifrelenmis hali gizli anahtar olmadan hesaplanamaz Temel Bilgiler Paillier sifrelemesi ile bazi ayrik logaritmalarin Ayrik logaritma kolay bir bicimde hesaplanabilecegi gosterilebilir Ornegin binom acilimi kullanarak 1 x n k 0n nk xk 1 nx n2 x2 higher powers of x displaystyle 1 x n sum k 0 n n choose k x k 1 nx n choose 2 x 2 higher powers of x dd Yukaridaki esitlikten 1 n x 1 nx modn2 displaystyle 1 n x equiv 1 nx pmod n 2 dd elde edilir Buradan eger y 1 n xmodn2 displaystyle y 1 n x mod n 2 dd ise x y 1n modn displaystyle x equiv frac y 1 n pmod n dd yazilabilir Yani L displaystyle L fonksiyonu L u u 1n displaystyle L u frac u 1 n tam sayi bolme isleminin bolumu seklinde tanimlanmak uzere ve x Zn displaystyle x in mathbb Z n iken L 1 n xmodn2 x modn displaystyle L 1 n x mod n 2 equiv x pmod n yazilabilir Anlamsal Guvenlik Yukarida belirtilen orijinal kriptosistem yukarida gosterildigi gibi secilmis acik metin saldirilarina karsi anlamsal guvenlik saglar Secilmis acik metin saldirisi Ayrica bakinizPaillier in tarihsel oncusu Okamoto Uchiyama sifreleme sistemi Paillier in genellestirilmis hali Paillier in etkilesimli simulatoru oylama uygulamasinin ornegidir Paillier sifrelemesinin etkilesimli demosu Kriptografik yontemler kullanilarak nasil oylama yapilabilecegini gosteren googletechtalk videosuNotlar a b Jonathan Katz Yehuda Lindell Introduction to Modern Cryptography Principles and Protocols Chapman amp Hall CRC 2007 Pascal Paillier PDF 6 Nisan 2012 tarihinde kaynagindan PDF arsivlendi 18 Subat 2012 18 Subat 2012 tarihinde kaynagindan arsivlendi Erisim tarihi 14 Ekim 2020 16 Subat 2012 16 Subat 2012 tarihinde kaynagindan arsivlendi Erisim tarihi 14 Ekim 2020 23 Aralik 2011 23 Aralik 2011 tarihinde kaynagindan arsivlendi Erisim tarihi 14 Ekim 2020 KaynakcaPaillier Pascal 1999 Public Key Cryptosystems Based on Composite Degree Residuosity Classes EUROCRYPT Springer pp 223 238 doi 10 1007 3 540 48910 X 16 Paillier Pascal Pointcheval David 1999 Efficient Public Key Cryptosystems Provably Secure Against Active Adversaries ASIACRYPT Springer pp 165 179 doi 10 1007 978 3 540 48000 6 14 Paillier Pascal 1999 Cryptosystems Based on Composite Residuosity Ph D thesis Ecole Nationale Superieure des Telecommunications Paillier Pascal 2002 PDF CryptoBytes 5 1 20 Ekim 2006 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 22 Mayis 2012 Dis baglantilar 29 Haziran 2012 tarihinde kaynagindan arsivlendi Paillier sifrelemesinin homomorfik ozellikleriyle beraber gelistirilmis halidir Paillier sifrelemesinin ve buna dayana kriptografik sayaclarin gelistirilmis halini iceren acik kaynak kutuphane
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans