Matematik dünyasında, Parseval teoremiFourier dönüşümünün bir üniter ifade olduğu sonucunu bize açıklar. Basit bir şekilde açıklarsak, bir fonksiyonun karesinin toplamı (ya da integrali) ile Fourier dönüşümün fonksiyonunun karesinin toplamının (ya da integrali) birbirine eşit olduğunu söyler. Teorem, 'in 1799 yılındaki seriler hakkındaki bir teoreminin Fourier serilerine uygulanması sonucu ortaya çıkmıştır. Lord Rayleigh ile John William Strutt'tan sonra Rayleigh Enerji Teoremi veya Rayleigh Özdeşliği olarak da bilinir.
"Parseval Teoremi" terimi, genelde herhangi bir Fourier dönüşümünün üniterliğini tanımlamak için kullanılsa da, özellikle fizikte bu özelliğin en genel biçimi şeklinde daha doğru bir şekilde ifade edersek bu teoremin adı 'dir.
Parseval Teoremi'nin Matematiksel İfadesi
Varsayalım ki 
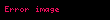


ile
şeklinde formüle edilebilir. Daha sonra ise;
|
Burada 

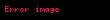
Yukarıda bulunan eşitliğin orta terimlerinde olduğu gibi periyodu 

Genel olarak, değişmeli yerel kompakt grup olan G Pontryagin İkiliği olan G^ şeklinde verildiğinde, Parseval Teoremi bize şunu söyler: Pontryagin-Fourier dönüşümü Hilbert uzayları olan L2(G) ve L2(G^) arasında üniter bir operatördür. G, birim çember T olduğunda, G^ tam sayıdır ve yukarıda tartışılan durum tam olarak budur. G reel sayılarda 

Parseval Teoremi şu şekilde de ifade edilebilir: 
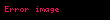


Daha sonra aşağıdaki formülü elde ederiz:
Mühendislikte kullanılan notasyon
Elektrik mühendisliğinde, Parseval Teoremi genellikle şu şekilde formüle edilir:
Burada 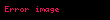


Bu teorem, bir sinyalin toplam enerjisinin, zamana göre örnek başına güç toplamının veya frekansa göre spektral gücün toplanması yoluyla hesaplanabileceğini ifade eder.
Ayrık zaman sinyalleri için teorem şöyle aşağıdaki şekilde yazılır:
Burada 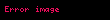



Alternatif olarak ayrık Fourier dönüşümü (DFT) şeklinde ifade etmek istersek eşitlik şu hale gelir:
Burada 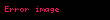
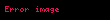
Aşağıda DFT'nin durumunu gösteriliyor. Diğer durumlar için de aynı ispat yolu izlenebilir. 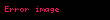
Bırada 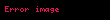
Kaynakça
- ^ Mémoires presentés a L'Institut des Sciences, Lettres et Arts, par divers savants èt lus dans ses assemblées : Sciences, Mathématiques et Physiques (Fransızca). Académie royale des sciences (France). s. 638-648. 20 Şubat 2023 tarihinde kaynağından . Erişim tarihi: 20 Şubat 2023.
- ^ Rayleigh, J.W.S. (1889). Philosophical Magazine, vol. 27 (İngilizce). s. 460-469. 20 Şubat 2023 tarihinde kaynağından . Erişim tarihi: 20 Şubat 2023.
- ^ Plancherel, Michel (1910). Contribution à l'etude de la representation d'une fonction arbitraire par les integrales définies (Fransızca). Rendiconti del Circolo Matematico di Palermo, vol. 30. s. 298-335.
- ^ Arthur E. Danese (1965). Advanced Calculus (İngilizce). 1. Boston, MA: Allyn and Bacon, Inc. s. 439.
- ^ Wilfred Kaplan (1991). Advanced Calculus. 4th. Reading, MA: Addison Wesley. s. 519. ISBN .
- ^ Georgi P. Tolstov (1962). Fourier Series. Silverman, Richard tarafından çevrildi. Englewood Cliffs, NJ: Prentice-Hall, Inc. s. 119.
Dış bağlantılar
- Parseval 1 Kasım 2019 tarihinde Wayback Machine sitesinde ., MacTutor History of Mathematics archive.
- George B. Arfken and Hans J. Weber, Mathematical Methods for Physicists (Harcourt: San Diego, 2001).
- Hubert Kennedy, Eight Mathematical Biographies 23 Ocak 2022 tarihinde Wayback Machine sitesinde . (Peremptory Publications: San Francisco, 2002).
- Alan V. Oppenheim and Ronald W. Schafer, Discrete-Time Signal Processing 2nd Edition (Prentice Hall: Upper Saddle River, NJ, 1999) p 60.
- William McC. Siebert, Circuits, Signals, and Systems (MIT Press: Cambridge, MA, 1986), pp. 410–411.
- David W. Kammler, A First Course in Fourier Analysis (Prentice–Hall, Inc., Upper Saddle River, NJ, 2000) p. 74.
- Mathworld Üzerine Parseval Teoremi 5 Eylül 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik dunyasinda Parseval teoremiFourier donusumunun bir uniter ifade oldugu sonucunu bize aciklar Basit bir sekilde aciklarsak bir fonksiyonun karesinin toplami ya da integrali ile Fourier donusumun fonksiyonunun karesinin toplaminin ya da integrali birbirine esit oldugunu soyler Teorem in 1799 yilindaki seriler hakkindaki bir teoreminin Fourier serilerine uygulanmasi sonucu ortaya cikmistir Lord Rayleigh ile John William Strutt tan sonra Rayleigh Enerji Teoremi veya Rayleigh Ozdesligi olarak da bilinir Parseval Teoremi terimi genelde herhangi bir Fourier donusumunun uniterligini tanimlamak icin kullanilsa da ozellikle fizikte bu ozelligin en genel bicimi seklinde daha dogru bir sekilde ifade edersek bu teoremin adi dir Parseval Teoremi nin Matematiksel IfadesiVarsayalim ki A x displaystyle A x ve B x displaystyle B x fonksiyonlari R displaystyle mathbb R reel sayilar kumesi icerisinde periyodu 2p displaystyle 2 pi olan karmasik degerli bir fonksiyondur Ayrica Fourier serisi seklinde periyot uzunluguna gore integrallenebilir kare fonksiyon olduklarini da goz onune alirsak asagidaki esitlikler karsimiza cikar A x n aneinx displaystyle A x sum n infty infty a n e inx ile B x n bneinx displaystyle B x sum n infty infty b n e inx seklinde formule edilebilir Daha sonra ise n anbn 12p ppA x B x dx displaystyle sum n infty infty a n overline b n frac 1 2 pi int pi pi A x overline B x mathrm d x Eq 1 Burada i displaystyle i sayisi sanal sayiyi ve yatay cizgi ise karmasik duzlemi ifade etmektedir A x displaystyle A x ve B x displaystyle overline B x yi esitlikte yerine koyarsak n anbn 12p pp n aneinx n bn e inx dx 12p pp a1ei1x a2ei2x b1 e i1x b2 e i2x dx 12p pp a1ei1xb1 e i1x a1ei1xb2 e i2x a2ei2xb1 e i1x a2ei2xb2 e i2x dx 12p pp a1b1 a1b2 e ix a2b1 eix a2b2 dx displaystyle begin aligned sum n infty infty a n overline b n amp frac 1 2 pi int pi pi left sum n infty infty a n e inx right left sum n infty infty overline b n e inx right mathrm d x 6pt amp frac 1 2 pi int pi pi left a 1 e i1x a 2 e i2x cdots right left overline b 1 e i1x overline b 2 e i2x cdots right mathrm d x 6pt amp frac 1 2 pi int pi pi left a 1 e i1x overline b 1 e i1x a 1 e i1x overline b 2 e i2x a 2 e i2x overline b 1 e i1x a 2 e i2x overline b 2 e i2x cdots right mathrm d x 6pt amp frac 1 2 pi int pi pi left a 1 overline b 1 a 1 overline b 2 e ix a 2 overline b 1 e ix a 2 overline b 2 cdots right mathrm d x end aligned Yukarida bulunan esitligin orta terimlerinde oldugu gibi periyodu 2p displaystyle 2 pi olan bircok terimin integrali 0 displaystyle 0 olacaktir Ayrica bakiniz Harmonik Seriler n anbn 12p a1b1 x ia1b2 e ix ia2b1 eix a2b2 x p p 12p 2pa1b1 0 0 2pa2b2 a1b1 a2b2 displaystyle begin aligned sum n infty infty a n overline b n amp frac 1 2 pi left a 1 overline b 1 x ia 1 overline b 2 e ix ia 2 overline b 1 e ix a 2 overline b 2 x cdots right pi pi 6pt amp frac 1 2 pi left 2 pi a 1 overline b 1 0 0 2 pi a 2 overline b 2 cdots right 6pt amp a 1 overline b 1 a 2 overline b 2 cdots 6pt end aligned Genel olarak degismeli yerel kompakt grup olan G Pontryagin Ikiligi olan G seklinde verildiginde Parseval Teoremi bize sunu soyler Pontryagin Fourier donusumu Hilbert uzaylari olan L2 G ve L2 G arasinda uniter bir operatordur G birim cember T oldugunda G tam sayidir ve yukarida tartisilan durum tam olarak budur G reel sayilarda R displaystyle mathbb R gercek dogru ise G de ayni zamanda reeldir R displaystyle mathbb R ve uniter donusum gercek dogru uzerindeki bir Fourier donusumdur G dongusel grup Zn oldugunda yine kendine esittir self dual burada ise Pontryagin Fourier donusumu uygulamada ayrik Fourier donusumu olarak adlandirilir Parseval Teoremi su sekilde de ifade edilebilir f x displaystyle f x Fourier serisi ile p p displaystyle pi pi arasinda integrallenebilir kare bir fonksiyondur yani hem f x displaystyle f x hem de f2 x displaystyle f 2 x de bu aralikta integrallenebilir f x a02 n 1 ancos nx bnsin nx displaystyle f x simeq frac a 0 2 sum n 1 infty a n cos nx b n sin nx Daha sonra asagidaki formulu elde ederiz 1p ppf2 x dx a022 n 1 an2 bn2 displaystyle frac 1 pi int pi pi f 2 x mathrm d x frac a 0 2 2 sum n 1 infty left a n 2 b n 2 right Muhendislikte kullanilan notasyonElektrik muhendisliginde Parseval Teoremi genellikle su sekilde formule edilir x t 2dt 12p X w 2dw X 2pf 2df displaystyle int infty infty x t 2 mathrm d t frac 1 2 pi int infty infty X omega 2 mathrm d omega int infty infty X 2 pi f 2 mathrm d f Burada X w Fw x t displaystyle X omega mathcal F omega x t fonksiyonu x t displaystyle x t fonksiyonunun surekli Fourier donusumunu normallestirilmis ve uniter formda temsil eder Acisal frekans w 2pf displaystyle omega 2 pi f ise birim zamandaki radyan sayisidir Bu teorem bir sinyalin toplam enerjisinin zamana gore ornek basina guc toplaminin veya frekansa gore spektral gucun toplanmasi yoluyla hesaplanabilecegini ifade eder Ayrik zaman sinyalleri icin teorem soyle asagidaki sekilde yazilir n x n 2 12p pp X2p ϕ 2dϕ displaystyle sum n infty infty x n 2 frac 1 2 pi int pi pi X 2 pi phi 2 mathrm d phi Burada X2p displaystyle X 2 pi x displaystyle x fonksiyonunun ayrik zamanli Fourier donusumudur DTFT ayrica ϕ displaystyle phi ise x displaystyle x in acisal frekansini radyan cinsinden temsil eder Alternatif olarak ayrik Fourier donusumu DFT seklinde ifade etmek istersek esitlik su hale gelir n 0N 1 x n 2 1N k 0N 1 X k 2 displaystyle sum n 0 N 1 x n 2 frac 1 N sum k 0 N 1 X k 2 Burada X k displaystyle X k x n displaystyle x n in DFT sini ifade eder Asagida DFT nin durumunu gosteriliyor Diger durumlar icin de ayni ispat yolu izlenebilir X k displaystyle X k in ters DFT sini kullanarak asagidaki esitligi turetebiliriz 1N k 0N 1 X k 2 1N k 0N 1X k X k 1N k 0N 1 n 0N 1x n exp j2pNkn X k 1N n 0N 1x n k 0N 1X k exp j2pNkn 1N n 0N 1x n N x n n 0N 1 x n 2 displaystyle frac 1 N sum k 0 N 1 X k 2 frac 1 N sum k 0 N 1 X k cdot X k frac 1 N sum k 0 N 1 left sum n 0 N 1 x n exp left j frac 2 pi N k n right right X k frac 1 N sum n 0 N 1 x n left sum k 0 N 1 X k exp left j frac 2 pi N k n right right frac 1 N sum n 0 N 1 x n N cdot x n sum n 0 N 1 x n 2 Birada displaystyle ifadesi Karmasik Sayinin Eslenigi ni temsil eder Kaynakca Memoires presentes a L Institut des Sciences Lettres et Arts par divers savants et lus dans ses assemblees Sciences Mathematiques et Physiques Fransizca Academie royale des sciences France s 638 648 20 Subat 2023 tarihinde kaynagindan Erisim tarihi 20 Subat 2023 Rayleigh J W S 1889 Philosophical Magazine vol 27 Ingilizce s 460 469 20 Subat 2023 tarihinde kaynagindan Erisim tarihi 20 Subat 2023 Plancherel Michel 1910 Contribution a l etude de la representation d une fonction arbitraire par les integrales definies Fransizca Rendiconti del Circolo Matematico di Palermo vol 30 s 298 335 Arthur E Danese 1965 Advanced Calculus Ingilizce 1 Boston MA Allyn and Bacon Inc s 439 Wilfred Kaplan 1991 Advanced Calculus 4th Reading MA Addison Wesley s 519 ISBN 0 201 57888 3 Georgi P Tolstov 1962 Fourier Series Silverman Richard tarafindan cevrildi Englewood Cliffs NJ Prentice Hall Inc s 119 Dis baglantilarParseval 1 Kasim 2019 tarihinde Wayback Machine sitesinde MacTutor History of Mathematics archive George B Arfken and Hans J Weber Mathematical Methods for Physicists Harcourt San Diego 2001 Hubert Kennedy Eight Mathematical Biographies 23 Ocak 2022 tarihinde Wayback Machine sitesinde Peremptory Publications San Francisco 2002 Alan V Oppenheim and Ronald W Schafer Discrete Time Signal Processing 2nd Edition Prentice Hall Upper Saddle River NJ 1999 p 60 William McC Siebert Circuits Signals and Systems MIT Press Cambridge MA 1986 pp 410 411 David W Kammler A First Course in Fourier Analysis Prentice Hall Inc Upper Saddle River NJ 2000 p 74 Mathworld Uzerine Parseval Teoremi 5 Eylul 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State