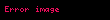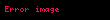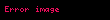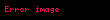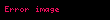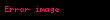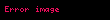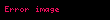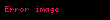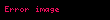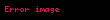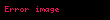Potansiyel kuyusu, bir parçacığın bağlı olması durumunu modelleyen sistemdir. Tek boyutta uygulanan potansiyel,
şeklinde verilir. Burada parçacık görüldüğü üzere a genişlikli sonsuz kuyunun içine hapsolmuştur. Parçacık için Schrödinger denklemi yazılırsa:
denklemin çözümü ise olarak elde edilir. Bu, parçacığı kuyu içinde temsil eden dalga fonksiyonudur. Uygulanan potansiyel sonsuz olduğu için parçacığın dışarıda bulunması olasılığı sıfır olacağından, dışarıdaki dalga fonksiyonu olur. Sınırlarda iki dalga fonksiyonunun değerlerinin alacağı değerler birbirine eşit olmak zorunda olduğundan sınır koşulları ortaya çıkar.
denklemi ile karşılaştırılırsa
elde edilir. Böylece bağlı durumdaki parçacıkların enerjilerinin kuantalandığı gösterilmiş olur zira parçacığın enerji seviyeleri olmak üzere bu enerjinin tam katlarıdır.
Diğer bir deyişle kuyudaki parçacığın enerjisi iki enerji seviyesi arasındaki enerjiyi alamaz. Bu yüzden enerjide süreksizlik vardır, bu duruma enerjinin kuantalanması denir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Potansiyel kuyusu bir parcacigin bagli olmasi durumunu modelleyen sistemdir Tek boyutta uygulanan potansiyel V x 0 0 lt x lt a diger displaystyle V x begin cases 0 amp 0 lt x lt a infty amp mbox diger end cases seklinde verilir Burada parcacik goruldugu uzere a genislikli sonsuz kuyunun icine hapsolmustur Parcacik icin Schrodinger denklemi yazilirsa d2psdx2 2mEℏ2ps displaystyle frac d 2 psi dx 2 frac 2mE hbar 2 psi d2psdx2 k2ps 0 I displaystyle frac d 2 psi dx 2 k 2 psi 0 mbox I k2 2mEℏ2 II displaystyle k 2 frac 2mE hbar 2 mbox II I displaystyle mbox I denklemin cozumu ise psic x Asin kx Bcos kx displaystyle psi mbox ic x A sin kx B cos kx olarak elde edilir Bu parcacigi kuyu icinde temsil eden dalga fonksiyonudur Uygulanan potansiyel sonsuz oldugu icin parcacigin disarida bulunmasi olasiligi sifir olacagindan disaridaki dalga fonksiyonu psdis x 0 displaystyle psi mbox dis x 0 olur Sinirlarda iki dalga fonksiyonunun degerlerinin alacagi degerler birbirine esit olmak zorunda oldugundan sinir kosullari ortaya cikar psic 0 psdis 0 0 displaystyle psi mbox ic 0 psi mbox dis 0 0 Asin 0 Bcos 0 0 B 0 displaystyle A sin 0 B cos 0 0 mbox B 0 psic x Asin kx displaystyle psi mbox ic x A sin kx psic a psdis a 0 displaystyle psi mbox ic a psi mbox dis a 0 Asin ka 0 displaystyle A sin ka 0 A 0 displaystyle A neq 0 mbox sin ka 0 displaystyle sin ka 0 ka np k npa displaystyle ka n pi mbox k frac n pi a II displaystyle mbox II denklemi ile karsilastirilirsa 2mEℏ2 k2 n2p2a2 displaystyle frac 2mE hbar 2 k 2 frac n 2 pi 2 a 2 En n2p2ℏ22ma2 n 1 2 3 displaystyle E n frac n 2 pi 2 hbar 2 2ma 2 mbox n 1 2 3 elde edilir Boylece bagli durumdaki parcaciklarin enerjilerinin kuantalandigi gosterilmis olur zira parcacigin enerji seviyeleri E0 p2ℏ22ma2 displaystyle E 0 frac pi 2 hbar 2 2ma 2 olmak uzere bu enerjinin tam katlaridir En n2E0 n 1 2 3 displaystyle E n n 2 E 0 mbox n 1 2 3 Diger bir deyisle kuyudaki parcacigin enerjisi iki enerji seviyesi arasindaki enerjiyi alamaz Bu yuzden enerjide sureksizlik vardir bu duruma enerjinin kuantalanmasi denir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State