Matematikte, Riemann toplamı genellikle fonksiyon eğrisinin altında kalan bölgenin yaklaşık alanıdır. Bu toplama, Alman matematikçi Bernhard Riemann'ın soyadı verilmiştir.

Toplama işlemi, bölgenin farklı şekillere bölünüp (dikdörtgenler ya da yamuklar) birlikte, fonksiyonun ölçülen bölgesine benzer bir alan çıkartılması, ardından da her bir şeklin alanının hesaplanması ve son olarak bütün bu küçük alanların toplanmasından oluşur. Böyle bir uzlaşım belirli integrallerin sayısal hesaplanmasında kullanılabilir. Ayrıca hesabın temel teoremi kapalı tür integral yazımına izin vermediği zaman da kullanılabilir.
Küçük şekillerle doldurulmuş bölgenin alanı tam olarak, ölçülmek istenen alana eşit olmadığı için Riemann toplamı gerçek alandan daha farklı çıkar. Bu hata, bölgeyi daha da küçük şekillere bölmekle giderilebilir. Şekiller küçüldükçe toplam, Riemann integraline yaklaşır.
Tanım
f : D → R fonksiyonunu reel sayılar, R, kümesinin D altkümesinde tanımlayalım. I = [a, b] ise D altkümesinde tanımlı kapalı bir aralık olsun ve
olarak I aralığının bir kesiti olsun ve de
olsun.
f fonksiyonun I altkümesindeki P kesiti Riemann toplamı şöyle tanımlanır:
Burada şuna dikkat edilmelidir ki, 


Örnek: 
- Eğer, bütün i değerleri için
ise, o zaman S sol Riemann toplamı olur.
- Eğer, bütün i değerleri için
ise, o zaman S sağ Riemann toplamı olur.
- Eğer, bütün i değerleri için
ise, o zaman da S orta değer Riemann toplamı olur.
- Sol ve sağ Riemann toplamlarının ortalaması ise yamuklu toplama olur.
- Eğer şöyle bir ifade verilmişse
- burada
,
aralığında f fonksiyonunun noktasıysa, o zaman S üstten Riemann toplamı olur.
- Benzer şekilde, eğer
,
aralığında f fonksiyonunun noktasıysa, o zaman da S alttan Riemann toplamı olur.
Verilen bir kesitteki herhangi bir Riemann toplamı (yani, 


Yöntemler





Riemann toplamının dört ana yöntemi, eşit kesit boyutları kullanılarak daha iyi anlaşılabilir. Yani, [a, b] aralığı n alt aralığa bölünür ve her bir aralığın uzunluğu
bağıntısıyla bulunur. Kesitlerdeki noktalar da
ile gösterilir.
Sol Riemann Toplamı
Sol toplam, dikdörtgenlerin sol uç noktalarının kullanılması ve Δx taban uzunluğu ile f(a + iΔx) dikdörtgen uzunluğu kullanılmasıyla hesaplanır. Bunu i = 0, 1, ..., n − 1 için yapıp çıkan alanları toplamak şu sonucu verir:
Eğer f fonksiyonu bu aralıkta bir şekildeyse sol Riemann toplamı gerçek değerden fazla bir sonuca götürür, fakat ise gerçek değerden daha düşük bir sonuç çıkartır.
Sağ Riemann Toplamı
Burada f fonksiyonun sağ sınır noktaları kullanılır. Bu da tabanı Δx olan ve yüksekliği f(a + iΔx) olan dikdörtgenler verir. Bu işlemi bütün i = 1, ..., n değerleri için yapmak ve çıkan sonuçları toplamak şunu verir
Eğer f fonksiyonu sağ Riemann toplamı gerçek değerden daha düşük bir sonuç verir, eğer da gerçek değerden daha büyük bir değer verir. Bu formüldeki hata şöyle bulunur
burada 

Orta Değer Riemann Toplamı
f fonksiyonunu, aralığın orta noktalarını kullanarak, boyları, birinci aralık için f(a + Q/2), ikincisi için f(a + 3Q/2) olan ve f(b − Q/2) kadar giden dikdörtgenler verir. Bunların alan toplamları şöyledir
Bu formülün hatası şöyledir
burada 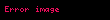

Yamuklu Toplama Kuralı
Bu yöntemde ise, f fonksiyonunun aralıktaki değerleri sol ve sağ sınır noktalarının ortalamasına denkleştirilir. Yukarıdakilerle aynı olarak, yamuk için alan formülünü kullanarak
b1, b2 paralel kenarlı ve h yükseklikli yamukların alanını hesaplayıp şu formülle bütün bu alanları toplamak mümkün olur
Bu formüldeki hata şöyle hesaplanır
burada da 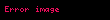

Yamuk yöntemiyle hesaplanan olası alan değeri sağ ve sol toplamların ortalamasına eşittir.
Örnek


Örnek olarak, y = x2 fonksiyonunun 0 ile 2 arasındaki eğri altında kalan alanı Riemann toplamı kullanılarak algoritmik bir şekilde hesaplanabilir.
İlk önce, [0, 2] aralığı n parçaya bölünür ve her birinin genişliği 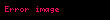




Her kutunun alanı 
olur.
Eğer n → ∞ iken, yukarıdaki toplama formülünün limiti alınırsa, artan kutuların alan toplamı değerinin, grafiğin altında kalan bölgenin gerçek alanına yaklaştığı fark edilir. Dolayısıyla:
Bu yöntem daha farklı yollarla hesaplanan belirli integral ile de uyuşmaktadır:
Animasyonlar
-
![image]() Sol Toplam
Sol Toplam -
![image]() Sağ Toplam
Sağ Toplam -
![image]() Orta Değer Toplamı
Orta Değer Toplamı -
![image]()
fonksiyonu için
Daha Fazlası
- Riemann integrali
- Lebesgue integrali
- Simpson Yöntemi
- Euler yöntemi and , diferansiyel denklem çözümüyle alakalı bazı yöntemler.
Kaynakça
- Thomas, George B. Jr.; Finney, Ross L. (1996), Calculus and Analytic Geometry (9th ed.), Addison Wesley, ISBN
Dış bağlantılar
- Riemann toplamlarının yakınsamasını gösteren bir simülasyon19 Şubat 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Riemann toplami genellikle fonksiyon egrisinin altinda kalan bolgenin yaklasik alanidir Bu toplama Alman matematikci Bernhard Riemann in soyadi verilmistir Riemann toplaminin dort farkli yontemi ile egri altindaki alanin yaklasik olarak hesaplanmasi Sag ve sol yontemleri her bir alt aralik icindeki sol ve sag sinir noktalarini kullanir Maksimum ve minimum yontemleri ise her bir alt aralik icindeki en buyuk ve en kucuk degerli sinir noktalarini kullanir Toplamlarin degerleri alt araliklar sol ustten sag alta yarilandikca yakinsamaya baslar Toplama islemi bolgenin farkli sekillere bolunup dikdortgenler ya da yamuklar birlikte fonksiyonun olculen bolgesine benzer bir alan cikartilmasi ardindan da her bir seklin alaninin hesaplanmasi ve son olarak butun bu kucuk alanlarin toplanmasindan olusur Boyle bir uzlasim belirli integrallerin sayisal hesaplanmasinda kullanilabilir Ayrica hesabin temel teoremi kapali tur integral yazimina izin vermedigi zaman da kullanilabilir Kucuk sekillerle doldurulmus bolgenin alani tam olarak olculmek istenen alana esit olmadigi icin Riemann toplami gercek alandan daha farkli cikar Bu hata bolgeyi daha da kucuk sekillere bolmekle giderilebilir Sekiller kuculdukce toplam Riemann integraline yaklasir Tanimf D R fonksiyonunu reel sayilar R kumesinin D altkumesinde tanimlayalim I a b ise D altkumesinde tanimli kapali bir aralik olsun ve P x0 x1 x1 x2 xn 1 xn displaystyle P left x 0 x 1 x 1 x 2 dots x n 1 x n right olarak I araliginin bir kesiti olsun ve de a x0 lt x1 lt x2 lt lt xn b displaystyle a x 0 lt x 1 lt x 2 lt cdots lt x n b olsun f fonksiyonun I altkumesindeki P kesiti Riemann toplami soyle tanimlanir S i 1nf xi xi xi 1 xi 1 xi xi displaystyle S sum i 1 n f x i x i x i 1 quad x i 1 leq x i leq x i Burada suna dikkat edilmelidir ki xi displaystyle x i degeri xi 1 xi displaystyle x i 1 x i araliginda istege bagli bir degerdir yani herhangi bir f fonksiyonu icin farkli Riemann toplamlari uretilebilir yeter ki xi 1 xi xi displaystyle x i 1 leq x i leq x i sarti saglansin Ornek xi displaystyle x i nin degisik secimleri farkli Riemann toplamlari verir Eger butun i degerleri icin xi xi 1 displaystyle x i x i 1 ise o zaman S sol Riemann toplami olur Eger butun i degerleri icin xi xi displaystyle x i x i ise o zaman S sag Riemann toplami olur Eger butun i degerleri icin xi 12 xi xi 1 displaystyle x i tfrac 1 2 x i x i 1 ise o zaman da S orta deger Riemann toplami olur Sol ve sag Riemann toplamlarinin ortalamasi ise yamuklu toplama olur Eger soyle bir ifade verilmisseS i 1nvi xi xi 1 displaystyle S sum i 1 n v i x i x i 1 dd burada vi displaystyle v i xi 1 xi displaystyle x i 1 x i araliginda f fonksiyonunun noktasiysa o zaman S ustten Riemann toplami olur Benzer sekilde eger vi displaystyle v i xi 1 xi displaystyle x i 1 x i araliginda f fonksiyonunun noktasiysa o zaman da S alttan Riemann toplami olur Verilen bir kesitteki herhangi bir Riemann toplami yani xi displaystyle x i icin xi 1 displaystyle x i 1 ve xi displaystyle x i araligindaki istenilen degeri ustten ve alttan Rieman toplamlarinin arasinda kalir Riemann integrallenmesi icin kesit daraldikca alttan ve ustten Riemann toplamlarinin birbirine hep yaklasmasi gerekir Bu bilgi hesabi icin kullanilabilir Yontemlerx3 fonksiyonunun 0 2 araligindaki Riemann toplama yontemleri Dort kesit kullanilarak yapilmistir SolSagOrtaYamukluSimpson yontemi ile Riemann toplaminin dort ana yontemi esit kesit boyutlari kullanilarak daha iyi anlasilabilir Yani a b araligi n alt araliga bolunur ve her bir araligin uzunlugu Dx b an displaystyle Delta x frac b a n bagintisiyla bulunur Kesitlerdeki noktalar da a a Dx a 2Dx a n 2 Dx a n 1 Dx b displaystyle a a Delta x a 2 Delta x ldots a n 2 Delta x a n 1 Delta x b ile gosterilir Sol Riemann Toplami Sol toplam dikdortgenlerin sol uc noktalarinin kullanilmasi ve Dx taban uzunlugu ile f a iDx dikdortgen uzunlugu kullanilmasiyla hesaplanir Bunu i 0 1 n 1 icin yapip cikan alanlari toplamak su sonucu verir Dx f a f a Dx f a 2Dx f b Dx displaystyle Delta x left f a f a Delta x f a 2 Delta x cdots f b Delta x right Eger f fonksiyonu bu aralikta bir sekildeyse sol Riemann toplami gercek degerden fazla bir sonuca goturur fakat ise gercek degerden daha dusuk bir sonuc cikartir Sag Riemann Toplami Burada f fonksiyonun sag sinir noktalari kullanilir Bu da tabani Dx olan ve yuksekligi f a iDx olan dikdortgenler verir Bu islemi butun i 1 n degerleri icin yapmak ve cikan sonuclari toplamak sunu verir Dx f a Dx f a 2Dx f b displaystyle Delta x left f a Delta x f a 2 Delta x cdots f b right Eger f fonksiyonu sag Riemann toplami gercek degerden daha dusuk bir sonuc verir eger da gercek degerden daha buyuk bir deger verir Bu formuldeki hata soyle bulunur abf x dx Asag M1 b a 22n displaystyle left vert int a b f x dx A mathrm sag right vert leq frac M 1 b a 2 2n burada M1 displaystyle M 1 f x displaystyle f prime x fonksiyonun mutlak degerinin o araliktaki maksimum degeridir Orta Deger Riemann Toplami f fonksiyonunu araligin orta noktalarini kullanarak boylari birinci aralik icin f a Q 2 ikincisi icin f a 3Q 2 olan ve f b Q 2 kadar giden dikdortgenler verir Bunlarin alan toplamlari soyledir Q f a Q2 f a 3Q2 f b Q2 displaystyle Q left f a tfrac Q 2 f a tfrac 3Q 2 cdots f b tfrac Q 2 right Bu formulun hatasi soyledir abf x dx Aorta M2 b a 324n2 displaystyle left vert int a b f x dx A mathrm orta right vert leq frac M 2 b a 3 24n 2 burada M2 displaystyle M 2 f x displaystyle f prime prime x fonksiyonun mutlak degerinin o araliktaki maksimum degeridir Yamuklu Toplama Kurali Bu yontemde ise f fonksiyonunun araliktaki degerleri sol ve sag sinir noktalarinin ortalamasina denklestirilir Yukaridakilerle ayni olarak yamuk icin alan formulunu kullanarak A 12h b1 b2 displaystyle A tfrac 1 2 h b 1 b 2 b1 b2 paralel kenarli ve h yukseklikli yamuklarin alanini hesaplayip su formulle butun bu alanlari toplamak mumkun olur 12Q f a 2f a Q 2f a 2Q 2f a 3Q f b displaystyle tfrac 1 2 Q left f a 2f a Q 2f a 2Q 2f a 3Q cdots f b right Bu formuldeki hata soyle hesaplanir abf x dx Ayamuk M2 b a 312n2 displaystyle left vert int a b f x dx A mathrm yamuk right vert leq frac M 2 b a 3 12n 2 burada da M2 displaystyle M 2 f x displaystyle f prime prime x fonksiyonun mutlak degerinin o araliktaki maksimum degeridir Yamuk yontemiyle hesaplanan olasi alan degeri sag ve sol toplamlarin ortalamasina esittir Orneky x2 fonksiyonun 0 ile 2 araligindaki sematik bir grafigi y x2 foksiyonunun 0 ile 2 araligindaki Riemann toplam degerleri from 0 to 2 Dikdortgenlerin saysisi arttikca sonuc tam olarak 8 3 degerine yaklasmaktadir Ornek olarak y x2 fonksiyonunun 0 ile 2 arasindaki egri altinda kalan alani Riemann toplami kullanilarak algoritmik bir sekilde hesaplanabilir Ilk once 0 2 araligi n parcaya bolunur ve her birinin genisligi 2n displaystyle tfrac 2 n kadardir bunlar Riemann dikdortgenlerinin bu noktadan sonra kutu denilecek enleridir Sag Riemann toplami kullanilacagi icin kutularin x koordinatlari dizisi x1 x2 xn displaystyle x 1 x 2 ldots x n seklinde olur Ayni sekilde kutularin uzunluk dizisi de x12 x22 xn2 displaystyle x 1 2 x 2 2 ldots x n 2 olur xi 2in displaystyle x i tfrac 2i n xn 2 displaystyle x n 2 esitliklerini goz onunde bulundurmak onemlidir Her kutunun alani 2n xi2 displaystyle tfrac 2 n times x i 2 olur ve de ninci sag Riemann toplami S 2n 2n 2 2n 2in 2 2n 2nn 2 8n3 1 i2 n2 8n3 n n 1 2n 1 6 8n3 2n3 3n2 n6 83 4n 43n2 displaystyle begin aligned S amp frac 2 n times left frac 2 n right 2 cdots frac 2 n times left frac 2i n right 2 cdots frac 2 n times left frac 2n n right 2 amp frac 8 n 3 left 1 cdots i 2 cdots n 2 right amp frac 8 n 3 left frac n n 1 2n 1 6 right amp frac 8 n 3 left frac 2n 3 3n 2 n 6 right amp frac 8 3 frac 4 n frac 4 3n 2 end aligned olur Eger n iken yukaridaki toplama formulunun limiti alinirsa artan kutularin alan toplami degerinin grafigin altinda kalan bolgenin gercek alanina yaklastigi fark edilir Dolayisiyla limn S limn 83 4n 43n2 83 displaystyle lim n to infty S lim n to infty left frac 8 3 frac 4 n frac 4 3n 2 right frac 8 3 Bu yontem daha farkli yollarla hesaplanan belirli integral ile de uyusmaktadir 02x2dx 83 displaystyle int 0 2 x 2 dx frac 8 3 AnimasyonlarSol Toplam Sag Toplam Orta Deger Toplami y x2 displaystyle y x 2 fonksiyonu icinDaha FazlasiRiemann integrali Lebesgue integrali Simpson Yontemi Euler yontemi and diferansiyel denklem cozumuyle alakali bazi yontemler KaynakcaThomas George B Jr Finney Ross L 1996 Calculus and Analytic Geometry 9th ed Addison Wesley ISBN 0 201 53174 7 Dis baglantilarRiemann toplamlarinin yakinsamasini gosteren bir simulasyon19 Subat 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans

























